|
|
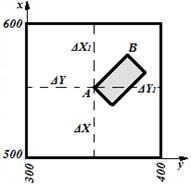
Сущность основных методов подготовки данных для выноса проекта на местность.12 Геодезическая подготовка данных для выноса проекта сооружения на местность – работы по получению разбивочного чертежа и разбивочных элементов с целью выноса и закрепления его основных осей в натуре. Перед выносом осей осуществляют расчет разбивочных данных и составляют разбивочный чертеж (схему) для разбивки. Способы геодезической подготовки данных для выноса проекта в натуру: 3.1. Графический - разбивочные элементы получают графически с топографического плана с точностью t =0,1 мм·М для линейных элементов и координат и 0,1 – 0,2º для дирекционных и разбивочных углов при измерении их геодезическим транспортиром. Так как обычно проектирование производится на копиях с топографических планов, то графическая точность будет еще ниже. Поэтому графический метод подготовки является наименее точным, но наиболее простым, быстрым и применяется в основном для неответственных или вспомогательных зданий и сооружений, а также внутриквартальной жилой застройки, где к точности планового положения объектов не предъявляют повышенных требований. Координаты точки А могут быть вычислены с учётом деформации бумаги:
Рис.1 Вычисление координат точки А с учетом деформации бумаги
Где X,Y - координаты нижнего угла координатной сетки, ΔX, ΔY; ΔX1, ΔY1 - приращения координат, определённые графически с плана; L – номинальная длина стороны координатной сетки (100 мм) 3.2. Аналитический - все данные для разбивки получают из расчетов; координаты осей сооружений получают из вычислительной обработки измерений на местности. Метод заключается в вычислении координат проектных точек, дирекционных углов и длин линий привязки к опорным пунктам. Например, вычисление координат точки А выполняется по известным координатам исходного пункта М, дирекционному углу α линии МА образующему разбивочный угол β, и длине разбивочного отрезка d из решения прямой геодезической задачи.
αMA = αMN + β; tg β = d =
Рис.2 Аналитический метод определения координат точки А 3.3. Графо-аналитический- комбинированный метод: часть данных получают графически, часть - из расчетов. Этот метод представляет собой сочетание аналитического и графического методов. Графически определяют координаты отдельных точек проектируемого объекта (например точки А), а значения координат остальных точек В, С, D и разбивочные элементы находят из решения прямой и обратной геодезических задач. При подготовке данных дня выноса проекта строительства все эти три метода применяются в совокупности и дополняют друг друга. Выбор метода и данные подготовки разбивочных чертежей зависят or точности разбивочных работ. 3.4. Типовые задачи при геодезической подготовке проекта: а). Определение координат точки пересечения двух линий, заданных координатами их концов. На практике встречается задача, когда необходимо рассчитать координаты точки пересечения двух створов. Створы заданы координатами их конечных точек, соответственно, створ A-С задан координатами точек А и С, створ В-D задан координатами точек В и D. Искомыми являются координаты точки О - точки пересечения створов.
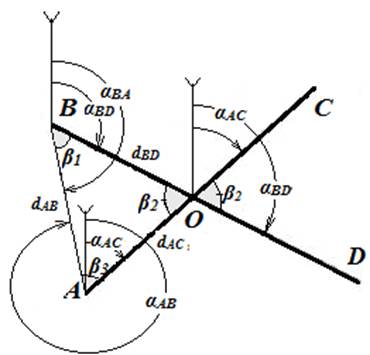
Рис.3 Схема определения координат точки пересечения двух линий, заданных координатами их концов. Порядок решения задачи: 1. по сторонам А-С, В-D, A-В решают обратные геодезические задачи (ОГЗ) и определяют дирекционные углы и длины отрезков 2. по дирекционным углам вычисляют углы в Δ АОВ β1 = αВА- αВD; β2 = αВD- αAC; β3 = αAC + 360º– αAB Правильность вычислений контролируют по формуле: β1 +β2 +β3 =180º00'.
3. используя β1; β2;β3 и отрезок dAB, по теореме синусов вычисляют отрезки dAО и dBO.
Контролем правильности вычислений служит соблюдение равенства: dAC = dAO + dCO . 4. находят координаты точки О из решения прямых геодезических задач (ПГЗ) от точек А и С по сторонам АО и СО соответственно. Контролем правильности вычислений служит совпадение дважды вычисленных координат точки О.
б). Определение координат створной точки. Задача возникает, когда в створе заданной линии необходимо вынести точки, лежащие на расстояниях, пропорциональных постоянной величине (например, шагу колонн).
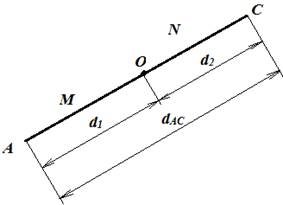
Рис.4 Схема определения координат створной точки
Исходными данными являются координаты (Xi , Yi) концов створных линий A-С, а также соотношение N : М, в котором должен быть разбит свор линии. Решение сводится к вычислению координат створной точки по формулам аналитической геометрии на плоскости: Х = (ХА · N + XC · M)/(M + N); Y = (YA· N + YC · M)/(M + N), X,Y - координаты створной точки О. Контролем правильности вычислений является соблюдение равенства: dAC = d1 + d2 ; dAC =
где ΔХ= ХС - ХА ; ΔY= YС - YА . d1 = d2 = в). Определение координат точки на перпендикуляре к линии.
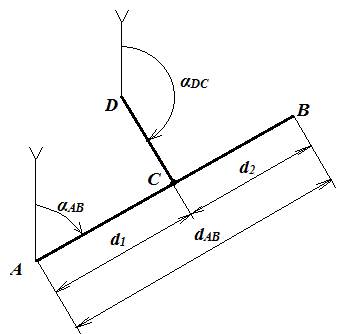
Рис.5 Схема определения координат точки на перпендикуляре к линии Если известны координаты точек А и В конца створа и точки С внутри створа, а также задана длина перпендикуляра, который должен быть построен из точки С до выносимой точки D, то расчёт координат точки D сводится к: · вычислению дирекционного угла αАВ линии АВ из обратной геодезической задачи между точками А и В; · вычислению дирекционного угла перпендикуляра CD: αDС = αАВ± 90º; · решению прямой геодезической задачи по стороне CD.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
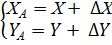
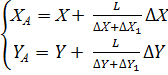

 ;
;
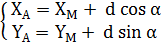

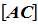 ,
,  ,
, 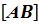 : αАС , αBD , αAB и dАС , dBD , dАB .
: αАС , αBD , αAB и dАС , dBD , dАB . =
= 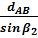 =
= 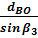
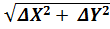 ,
,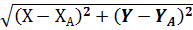 ;
; .
.