
|
|
Основное уравнение гидростатикиГидростатическое давление и его свойства
Выделим в пространстве, занимаемом жидкостью, массу жидкости, ограниченную поверхностью произвольной формы.
Массу жидкости разделим на две части плоскостью АВ. Воздействие верхней части I на нижнюю часть II заменим силой Р. Выделим в плоскости АВ площадку ∆F. Сила, действующая на эту площадку, равна ∆Р. Напряжение от этой силы в точке равно:
Величину р называют гидростатическим давлением в точке, или просто гидростатическим давлением. Оно обусловлено действием массовых сил, приложенных к частицам жидкости. Его единица [р] = Н/м2 = Па.
Гидростатическое давление отличается двумя свойствами: 1. Гидростатическое давление направлено по внутренней нормали к площадке, на которую оно действует. Если поверхность криволинейная, то давление направлено нормально к касательной этой поверхности. Это свойство связано с тем, что жидкость, находящаяся в состоянии равновесия, не сопротивляется растягивающим и сдвигающим усилиям. Гидростатическое давление является сжимающим усилием и направлено нормально к площадке, а не от нее, т. е. по внутренней нормали. 2. Гидростатическое давление в точке жидкости одинаково по всем направлениям или, иначе, гидростатическое давление не зависит от ориентации площадки, на которую оно действует.
Дифференциальные уравнения равновесия жидкости В разных точках давление р имеет неодинаковое значение, т. е. р = р (х, у, z) Основная задача гидростатики — исследование распределения давления в жидкости и на границах между жидкостью и различными поверхностями. Рассмотрим равновесие массы жидкости в объеме элементарного прямоугольного параллелепипеда.
Действие окружающей параллелепипед жидкости на его грани заменим силами давления жидкости с учетом свойств гидростатического давления. Пусть давление в точке, находящейся в центре параллелепипеда, равно р. Кроме давлений, действует массовая сила. Проекции этой силы, отнесенной к массе, т. е. ускорения, обозначим X, Y, Z. Поскольку давление является непрерывной функцией, то, разложив ее в ряд Тейлора и принимая во внимание два члена, найдем выражение для давлений на всех шести боковых гранях параллелепипеда. Чтобы не осложнять рисунок, такие давления Сумма проекций сил на оси х: Произведя сокращения, получим:
В то же время:
где mX – проекция массовой силы на ось х, V – объём жидкости
Отсюда следует: изменение давления рна единицу длины в каком-нибудь направлении (в данном случае в направлении оси х) равно проекции массовой силы, отнесенной к объему жидкости.
Аналогичные уравнения получим, проектируя силы на ось y и на ось z. Окончательно три уравнения равновесия запишем в виде:
Основное уравнение гидростатики Умножим систему уравнений соответственно на dх, dу, dz ирезультат их суммирования запишем в виде:
Левая часть уравнения есть полный дифференциал давления р, поэтому уравнение принимает вид:
Сумма в скобках правой части уравнения выражает энергию, отнесенную к массе. Выражение в скобках в правой части уравнения при ρ = const есть полный дифференциал некоторой функции U (х, у, z), т. е.:
С учетом этого уравнение принимает вид:
Функцию U (х, у, z) называют потенциалом массовых сил, или силовой функцией. Силы, для которых существует эта функция, называют силами, имеющими потенциал. Проинтегрируем уравнение (1). Будем считать, что жидкость находится под действием силы веса и ось z направлена вверх.
Ось у направлена перпендикулярно к плоскости чертежа.
При этих условиях: X = 0; Y = 0; Z = - g, где g — ускорение свободного падения.
С учетом этого уравнение (1) принимает вид:
На свободной поверхности жидкости в резервуаре давление р0. Давление в любой точке жидкости равно р. Уравнение (2) с учетом пределов интегрирования, как показано на рисунке, запишем так:
Поделим это выражение на γи полученный результат запишем со следующей группировкой членов:
Левая часть уравнения относится к точке, в которой давление р, а правая — к точке на поверхности воды, где давление р0 . Уравнение (4) — основное уравнение гидростатики.
Геометрический и энергетический смысл основного уравнения гидростатики
Геометрический смысл уравнения (4): - величина z фиксирует положение точки по отношению к плоскости хОу, называемой плоскостью сравнения. - ординату z называют высотой положения, или геометрической высотой.
При р = р0 имеем z = z0. Очевидно, что величина р/у имеет линейную размерность. Она представляет собой высоту, на которую жидкость может подняться под влиянием давления. Эту высоту можно измерить. если поместить в жидкость вертикальную закрытую сверху трубку, из которой полностью выкачан воздух. Высоту р/у называют высотой давлен и я, или приведенной высотой. Она представляет собой высоту столба жидкости, вес которого при давлении, равном нулю на его свободной поверхности, уравновешивает давление в данной точке жидкости. Чтобы пояснить энергетический смысл членов уравнения (4), введем понятие удельной энергии. Энергию, отнесенную к единице веса жидкости, называют удельной энергией. Размерность удельной энергии равна размерности энергии (работы), деленной на размерность силы. Единица удельной энергии [Е] — м. Часть удельной потенциальной энергии частицы жидкости, зависящая только от ее положения относительно условной горизонтальной плоскости, количественно равной z, называется удельной энергией положения частицы. Часть удельной потенциальной энергии частицы жидкости, зависящую только от ее давления, количественно равную р/у, называют удельной энергией давления частицы. Сумма Наряду с этими понятиями в гидравлике широко используется понятие напора. Так, величину z называют геометрическ и м напором в данной точке жидкости, а сумму z+р/γ=Н — гидростатическим напором. Перепишем уравнение (3) в виде
p - p0 = γ (z0 - z) = γh, откуда p = p0 + γh , (5) где h - глубина погружения частицы жидкости под ее поверхность.
Это уравнение, так же как и (4), называют основным уравнением гидростатики. Разница между ними только в системе отсчета вертикальных расстояний (z и h). Форма уравнения (4) удобна при изучении движения жидкости, так как сумма z + р/γ входит в уравнение движения жидкости. Форма уравнения (5) удобна в расчетах давления на поверхности и в методике измерения давления в жидкости. Величина р является абсолютным, или полным, давлением, р0 - внешним (начальным) давлением. Произведение γh — вес столба жидкости высотой h с площадью основания, равной единице. Поэтому γh можно назвать весовым давлением. Единицей давления, входящего в формулу (5), является паскаль (Па).
З акон Паскаля
Из формулы (5) следует, что давление р0 действует одинаково в любой точке внутри жидкости, и с изменением давления р0 на какое-либо значение на то же значение изменится и полное гидростатическое давление. Отсюда следует закон Паскаля: давление, приложенное на граничной поверхности жидкости, находящейся в равновесии в замкнутом резервуаре, передается всем частицам жидкости по всем направлениям без изменения. Действие многих гидравлических машин основано на законе Паскаля. Существует оригинальное приложение этого закона. Предположим, что требуется обжать какое-нибудь тело с одинаковой во всех его точках силой. Поместив тело в замкнутый резервуар с жидкостью и приложив силу к граничной поверхности жидкости, получим равномерное по всей поверхности сжатие тела.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


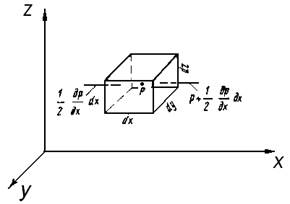
 показаны только в направлении оси х.
показаны только в направлении оси х. 

 ,
,



 (1)
(1)




 (2)
(2)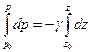
 (3)
(3) (4)
(4) представляет собой удельную потенциальную энергию частицы.
представляет собой удельную потенциальную энергию частицы.