
|
|
Определение критического сопротивления и чувствительности гальванометра к напряжению12
Для этого упражнения используется та же электрическая цепь (см. схему на рис.1), но другие начальные установки (см. рекомендации к упр.2). Измерения.1.С помощью потенциометра R получить отклонение “зайчика” на 50…60 делений шкалы. 2.Разомкните переключатель П и наблюдайте характер движения “зайчика” к нулю. Если “зайчик” совершает колебания около нулевого положения, то следует уменьшать сопротивление R1 до тех пор, пока при замыкании и размыкании переключателя колебания “зайчика” около положений равновесия не исчезнут. В то же время движение “зайчика” должно быть наиболее быстрым. Но тогда он может несколько проскакивать положение равновесия. Опытные экспериментаторы считают, что регулировку сопротивления R1 следует прекратить, если “зайчик” переходит положение равновесия не более половины деления шкалы (не более ½ мм). Выходит, метод субъективен. Значение сопротивления R1, на котором остановились, выбирая оптимальный характер движения “зайчика”, обозначим R1к. При этом в цепи гальванометра находится не только данное сопротивление, но еще и сопротивление самого гальванометра r, а также сопротивление R2. Сумма этих трех сопротивлений составляет так называемое критическое сопротивление Rкр, обеспечивающее самое благоприятное перемещение “зайчика”: кратчайшее время приближения к положению равновесия и отсутствие колебаний около него. Гальванометр с критическим сопротивление наилучшим образом подходит для измерения не только стационарного, но и изменяющегося со временем тока. Rкр = R1к+ R2 + r. (9) Поскольку наиболее благоприятные условия работы гальванометра – это доведение сопротивления в его цепи до критического, то можно оценить чувствительность гальванометра по напряжению, исходя из величины Rкр. Чувствительностью гальванометра по напряжению SU называется физическая величина, равная числу делений, на которое отклоняется указатель под действием напряжения 1 В. Чувствительностью SU связана с чувствительностью по току SI и критическим сопротивлением следующим образом:
Постоянной по напряжению называется обратная величина
Упражнение 3 Определение периода и логарифмического декремента затухания колебаний рамки
Измерения.1.Установите начальные значения сопротивлений согласно рекомендациям к упр.3. 2.С помощью потенциометра R получите отклонение «зайчика» 80-100 мм. 3.Разомкните выключатель В2 (сопротивление в цепи гальванометра при этом становится бесконечно большим), «зайчик» вернется к нулю шкалы и совершит при этом несколько затухающих колебаний. Определите по секундомеру продолжительность 2-3 полных колебаний с целью определить их «период». Повторите эту процедуру не менее трех раз, чтобы иметь возможность найти среднее значение периода свободных колебаний Т0 и их циклическую частоту w0=2p/Т0 . 4.Измерьте наибольшие отклонения двух следующих друг за другом колебаний «зайчика» Ак и Ак+1 по одну сторону от нуля (лучше – справа). По измеренным результатам определите логарифмический декремент затухания колебаний d¥ рамки гальванометра при бесконечном сопротивлении.
5.Замкните В2, теперь цепь гальванометра содержит установленное вначале сопротивление R1, а также R2 и r другие. Включая и выключая ток в гальванометре переключателем П, снимите зависимость логарифмического декремента затухания по мере уменьшения R1 до тех пор, пока колебания «зайчика» имеют место. Результаты запишите в табл.2.
Таблица 2
6.Постройте график зависимости 1/d=f(R1). Следует ожидать [2] линейный вид этой зависимости. Если экстраполировать график 1/d ® 0, то он пересекает ось абсцисс при R1® R1к , что дает возможность определить критическое сопротивление (9) еще одним способом. Действительно, при критическом сопротивлении в цепи гальванометра движение рамки к положению равновесия происходит без колебаний, апериодически, что можно интерпретировать как «колебания» с очень большим декрементом затухания. Rкр = R1к+ R2 + r. Сравнить критическое сопротивление, определенное этим способом и тем, который использован в упр.2. Упражнение 4 Определение баллистической постоянной гальванометра Баллистический режим работы гальванометра (на физическом жаргоне – баллистический гальванометр, здесь уместна аналогия с баллистическим маятником) применяется для измерения величины электрического заряда q, прошедшего по цепи при кратковременном импульсе тока, например, при разряде конденсатора. Предполагается, что длительность импульса много меньше периода свободных колебаний рамки гальванометра [3,4]. При таком допущении очевидно, что весь заряд пройдет через рамку за столь короткое время, что она не успеет отклониться. Рамка, однако, при этом получает толчок, от величины которого зависит угол, на который она повернется, значит угол b пропорционален заряду q.
где Из формулы (13) вытекает определение баллистической постоянной
Баллистическую постоянную можно определить экспериментально, используя для этого конденсатор с известной емкостью С0 (эталонный), включив его в электрическую цепь, схема которой приведена на рис.2. Эталонный конденсатор заряжается до разности потенциалов U0 от источника тока (переключатель П в положении 1), затем разряжается через гальванометр G(переключатель П в положении 2). Электрический заряд q=C0U0 (15) протекает через рамку гальванометра. Подставляя заряд (15) в формулу (14), получим выражение для определения баллистической постоянной:
Если вместо конденсатора С0 включить другой конденсатор с неизвестной емкостью С1 и зарядить его до разности потенциалов U1, то знание баллистической постоянной дает возможность определить емкость С1 по формуле
Измерения.1.Замкните демпфер Вд в целях предохранения гальванометра. 2.Соберите электрическую цепь по схеме (рис.2) и предложите преподавателю или лаборанту проверить ее. 3.Замкните выключатель В1 и установите напряжение U0 =0,50 В. 4.Переключателем П подключите конденсатор к источнику питания (переключатель в положении 1), в результате чего он зарядится до 0,50 В. 5.Разомкните демпфер Вд и проверьте, находится ли световой указатель на нулевой отметке шкалы. Если нет, то добейтесь этого. Как это можно сделать? 6.Переведите переключатель в положение 2 и засеките на шкале наибольшее отклонение «зайчика» – n0. 7.Результаты измерений n0 при трех различных напряжениях U0 внесите в табл.3. Таблица 3
8.Включите вместо С0 конденсатор неизвестной емкости С1 и проведите с ним аналогичные измерения баллистических отбросов n1 (п.3-6). 9.Обработка результатов сводится к вычислению баллистической постоянной по формуле (16) и определение емкости С1 по формуле (17), а также определению ширины доверительного интервала по Стьюденту. 10.Проверьте, выполняется ли следующее равенство:
Его существование обосновано в пособии [2], там это формула (66). Напоминаем также, что СI – чувствительность к току, T0 – период свободных колебаний рамки (см. упр.1 и 3). Эта проверка является одним из элементов контроля за правильностью измерений и вычислений параметров гальванометра.
Упражнение 5 Определение баллистической постоянной Когда к гальванометру присоединен конденсатор, то сопротивление этой цепи действительно очень большое. Но возможна и другая ситуация.
R1= Rкр – (r+r1). Рассмотрим реакцию гальванометра на импульс тока в цепи, обладающей критическим сопротивлением. Если в катушке L1 с числом витков w1 за dt секунд изменить магнитный поток на df, то в катушке будет наведена ЭДС индукции.
Возникший под действием ее индукционный ток i создаст в катушке L1 ЭДС самоиндукции
Согласно второму правилу Кирхгофа алгебраическая сумма падений напряжения в замкнутом контуре равна алгебраической сумме ЭДС.
Разделив переменные и проинтегрировав получившееся уравнение, будем иметь следующее решение:
где q=it – суммарный электрический заряд, прошедший по цепи (в том числе и через гальванометр) за время действия импульса тока длительностью t, f2-f1 – изменение магнитного потока за время t. Отсюда можно узнать величину заряда,
Прохождение заряда q через гальванометр вызывает поворот рамки на угол b, пропорциональный заряду,
Приравнивая выражения (19) и (20), получим для баллистической постоянной гальванометра в цепи, имеющей критическое сопротивление, следующую формулу:
Баллистические постоянные гальванометра
Как найти При прохождении тока I по соленоиду создается магнитное поле, напряженность которого на оси соленоида равна Н, индукция В и магнитный поток f
где l0 , S0 – длина и площадь поперечного сечения соленоида. Такой же магнитный поток пронизывает и вторую катушку L1, обозначим его f1. Если направление тока в соленоиде изменить на противоположное, то магнитный поток изменит знак f2 = – BS0. Таким образом, изменение магнитного потока через вторую катушку равно
а после подстановки
Выражение для баллистической постоянной (21) можно записать в виде:
Знак минус опущен, так как он определяет, в какую сторону повернется рамка гальванометра, но не влияет на величину угла поворота. Величина
называется баллистической постоянной по магнитному потоку. Измерения. 1.Соберите электрическую цепь по схеме на рис.3, включив в нее в качестве катушки L1 одну их четырех секций, содержащую w1 витков. Демпфер Вд при сборке как всегда должен быть замкнут. 2.Предложите преподавателю или лаборанту проверить собранную цепь. 3.Установите на магазине R1 критическое сопротивление. 4.Установите в цепи соленоида небольшой ток I, потом его, возможно, придется изменить. 5.Переводя переключатель П из одного положения в другое, измерьте максимальный баллистический отброс «зайчика» n. Это надо сделать при трех различных токах I. Результаты впишите в табл.4. Таблица 4
6.Вычислите 7.На основании результатов, полученных в упр. 1…5, сделайте сводную таблицу метрологических параметров исследованного гальванометра.
Сводка метрологических параметров гальванометра М17, № ………….
Упражнение 6 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (10)
. (10) . (11)
. (11) . (12)
. (12) и электроёмкости конденсатора
и электроёмкости конденсатора , (13)
, (13) , (14)
, (14) где n – максимальное число делений шкалы, на которое отклоняется «зайчик» при “проскакивании” через рамку заряда q (первый баллистический отброс).
где n – максимальное число делений шкалы, на которое отклоняется «зайчик» при “проскакивании” через рамку заряда q (первый баллистический отброс).
 . (16)
. (16) . (17)
. (17) .
.
 Пусть к гальванометру присоединена катушка, в которой возбуждается короткий импульс. В этом случае импульс проходит по цепи, в том числе и через гальванометр, но сопротивление ее не такое большое как с конденсатором, скорее даже малое. Рассмотрим цепь, схема которой приводится на рис.3. В цепь гальванометра входит катушка с индуктивностью L1 и активным сопротивлением r1, а также магазин сопротивлений R1. Приведенная схема отличается от рассмотренной выше (упр.4) тем, что здесь сопротивление в цепи гальванометра во-первых, не бесконечное и таковым оно быть не может, во-вторых, его можно изменять за счет R1. А это значит, что в зависимости от величины сопротивления характер движения рамки к положению равновесия и около него становится разным и этот выбор в руках экспериментатора. В данных условиях наиболее благоприятным является релаксационное движение критического характера. Для этого сопротивление цепи гальванометра должна быть критическим Rкр, величина которого определена в упр. 2 и 3. Поэтому на магазине R1 надо установить
Пусть к гальванометру присоединена катушка, в которой возбуждается короткий импульс. В этом случае импульс проходит по цепи, в том числе и через гальванометр, но сопротивление ее не такое большое как с конденсатором, скорее даже малое. Рассмотрим цепь, схема которой приводится на рис.3. В цепь гальванометра входит катушка с индуктивностью L1 и активным сопротивлением r1, а также магазин сопротивлений R1. Приведенная схема отличается от рассмотренной выше (упр.4) тем, что здесь сопротивление в цепи гальванометра во-первых, не бесконечное и таковым оно быть не может, во-вторых, его можно изменять за счет R1. А это значит, что в зависимости от величины сопротивления характер движения рамки к положению равновесия и около него становится разным и этот выбор в руках экспериментатора. В данных условиях наиболее благоприятным является релаксационное движение критического характера. Для этого сопротивление цепи гальванометра должна быть критическим Rкр, величина которого определена в упр. 2 и 3. Поэтому на магазине R1 надо установить .
. .
. . (18)
. (18) ,
, . (19)
. (19)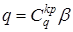 . (20)
. (20) . (21)
. (21) и
и  . (22)
. (22) ,
, , (23)
, (23) . (24)
. (24) [Кл/(мм/м)]. (25)
[Кл/(мм/м)]. (25) [Вб/(мм/м)] (26)
[Вб/(мм/м)] (26)
