
|
|
Определение коэффициента вязкости жидкости методом Стокса.12 Определение коэффициента вязкости жидкости методом Стокса.
Цель работы: экспериментальное определение коэффициента вязкости жидкости методом Стокса. Приборы, принадлежности и материалы: сосуд с исследуемой жидкостью, стальной шарик, секундомер, микрометр, денсиметр, линейка.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ Наблюдается два вида течение жидкости (газа). В одних случаях жидкость как бы разделяется на слои, которые скользят друг относительно друга, не перемешиваясь. Такое течение называется л а м и н а р н ы м (слоистым). Частицы жидкости в ламинарном потоке не переходят из одного слоя в другой. Ламинарное течение стационарно. При чем для него характерно то, что каждый слой движется с какой-то определенной скоростью υ. При небольших скоростях течения жидкости по трубе наблюдается ламинарное течение. Характер изменения скорости течения с расстоянием от оси трубы изображен на рис.1
Ламинарное течение Турбулентное течение При увеличении скорости потока характер течения существенно изменяется. Возникает энергичное перемешивание жидкости, в результате чего внутри жидкости появляются вихри - турбулентности. Такое течение называется т у р б у л е н т н ы м. «Профиль» скоростей внутри турбулентного потока изображен на рис.2. При турбулентном течении скорость в каждой точке сечения трубы приобретает некое значение. И только вблизи стенок скорость несколько изменяется. ДИНАМИЧЕСКАЯ ВЯЗКОСТЬ Вследствие того, что ламинарный поток как бы расслаивается, и каждый слой движется с определенной скоростью, то в процессе движения между слоями возникает трение, которое применительно к жидкостям и газам называется внутренним трением. Внутренне трение характеризуется коэффициентом, который называется динамической вязкостью. Динамическая вязкость обозначается греческой буквой η («эта») и измеряется в системе СИ в Паскалях-секунда: [η]=Па·с. Свойства динамической вязкости: · вязкость жидкостей резко уменьшается с повышением температуры жидкости; · вязкость газов наоборот резко увеличивается с повышением температуры газа. Кроме динамической вязкости, применяется еще понятие кинематической вязкости − это отношение динамической вязкости к плотности среды (жидкости или газа):
Единица измерения кинематической вязкости: [ν]= м2/с (иногда эту единицу измерения называют «Стоксом»: 1 Ст= 1 м2/с). ЗАКОН СТОКСА Стокс установил следующую закономерность: для тела, находящегося в ламинарном потоке, сила сопротивления среды пропорциональна коэффициенту динамической вязкости η, скорости υ движения тела относительно жидкости и характерному размеру тела l. Если тело имеет сферическую форму, то сила сопротивления потока будет равна: Fc=6πηrυ. где r– радиус тела, υ – относительная скорость тела (потока). Как и любая другая сила трения, Fc всегда направлена в сторону противоположную движению тела. МЕТОД СТОКСА На законе Стокса основано определение вязкости жидкости вискозиметром Гёпплера: в трубку определенногодиаметра, заполненную жидкостью, вязкость которой надо определить, опускают шарик и измеряют скорость его падения, которая и является мерой вязкости жидкости. Этот метод измерения вязкости называется методом Стокса и именно его мы будем применять в данной лабораторной работе. На металлический шарик массой m падающий в вязкой жидкости, действуют следующие силы (рис.3):
Fс=6πrηv,
1 ρж – плотность жидкости.
Тогда:
ЛАБОРАТОРНАЯ РАБОТА № 5 Определение коэффициента вязкости жидкости методом Стокса.
Цель работы: экспериментальное определение коэффициента вязкости жидкости методом Стокса. Приборы, принадлежности и материалы: сосуд с исследуемой жидкостью, стальной шарик, секундомер, микрометр, денсиметр, линейка.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Измерить диаметр шарика и определить его радиус r. 2. Измерить денсиметром плотность жидкости ρж. 3. Измерить температуру жидкости tºC. 4. Опустить шарик в жидкость и одновременно измерить секундомером время t прохождения шариком двух меток. 5. Измерить расстояние 1 между метками. 6. Опыт повторить 3 раза. 7. По формуле 8. Определить среднее значение коэффициента вязкости: ηср= 9. Определить абсолютную погрешность опыта:
10. Определить среднее значение абсолютной погрешности: 11. Определить относительную погрешность опыта: 12. Определить кинематическую вязкость жидкости: 13. Результаты измерений и вычислений занести в таблицу:
КОНТРОЛЬНЫЕ ВОПРОСЫ: 1. Что такое вязкость? Какова причина вязкости? 2. От чего зависит вязкость? В чем отличие вязкости жидкости от вязкости газов? 3. Закон Стокса (формулировка и формула) 4. Какие силы действуют на шарик, падающий в жидкости, и как они направлены?
ЗАДАЧИ: 1. Какую максимальную скорость будет кметь дождевая капля диаметром d= 0,5 см, если динамическая вязкость воздуха η=1,2·10-5 Па·с? (Плотность воды считать равной ρ=103 кг /м3). 2. Пробковый щарик всплывает в сосуде с глицерином. Чему рамен діаметр шарика, если известно, что шарик всплывает с постоянной скоростью υ=2 см/с, а динамическая вязкость глицерина в условиях опыта равна η = 1,48 Па·с? плотность пробки ρ1=200 кг/м3, а плотность глицерина ρ2=1200 кг/м3. 3. Шарик всплывает с постоянной скоростью в жид кости, плотность которой в 4 раза більше плотности шарика. Во сколько раз сила внутреннего трения жид кости Fс, которая действует на шарик, більше силы тяж ести?
РАБОЧИЙ ЛИСТ Ф.И.О:____________________________ группа__________ дата ___________
Вариант № ____
ЛАБОРАТОРНАЯ РАБОТА № 5 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
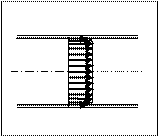
 Рис.1 Рис.2
Рис.1 Рис.2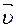
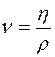 .
. .
.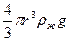 .
. Рис.3 где v – скорость движения шарика, g = 9,8 м/с2 – ускорение свободного падения,
Рис.3 где v – скорость движения шарика, g = 9,8 м/с2 – ускорение свободного падения, V =
V = 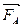 ρт – плотность материала шара,
ρт – плотность материала шара, Уравнение движения тела: F = FА + Fс.
Уравнение движения тела: F = FА + Fс.  ,
, Откуда:
Откуда:  . Поскольку
. Поскольку  , то
, то  .
. .
.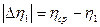 ;
;  ;
;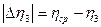
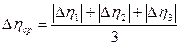
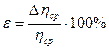
 .
.