
|
|
Расчет прочности элементов по наклонным сечениямНа приопорных участках под действием поперечной силы и изгибающего момента в сечениях, наклонных к продольной оси элемента, развиваются напряженно-деформированные состояния, как и в нормальных сечениях. Главные растягивающие и главные сжимающие напряжения действуют под углом к оси (рис. 36).
а) б) Рис. 36. Линии главных сжимающих и растягивающих напряжений.
Если главные растягивающие напряжения
Рис. 37. Схема разрушения элемента По наклонному сечению.
Разрушение изгибаемого элемента по наклонному сечению происходит по одному из трех возможных случаев: 1. Раздробление бетона наклонной сжатой полосы между наклонными трещинами (рис. 38). Происходит при малой ширине сечения, когда главные сжимающие напряжения превышают расчетное сопротивление бетона сжатию Rb.
где Если условие не соблюдается, необходимо увеличить размеры сечения или повысить класс бетона. 2. Сдвиг по наклонному сечению от действия поперечной силы (рис. 39).
Образование наклонной трещины происходит при При разрушении происходит взаимное смещение частей элемента по вертикали. Расчет прочности наклонных сечений на действие поперечной силы производят в обязательном порядке.
Т.е. если При расположении сосредоточенной силы F близко к опоре (a/h ≤ 1….1,5) трещиностойкость наклонных сечений увеличивается тем больше, чем ближе сила F к опоре.
3. Излом по наклонному сечению от действия изгибающего момента (рис. 40).
Расчет прочности по наклонным сечениям на действие поперечной силы элементов с поперечной арматурой (рис. 41).
Прочность элемента по наклонному сечению на действие поперечной силы элементов с поперечной арматурой обеспечивается условием:
Qb – поперечное усилие, воспринимаемое бетоном, определяется по формуле:
где:
Значение
Поперечные усилия Железобетонные элементы редко армируются отгибами, поэтому в частном случае Для элементов с поперечной арматурой в виде хомутов, нормальных к продольной оси элемента и имеющих постоянных шаг s в пределах рассматриваемого наклонного сечения, значение с0 соответствует минимуму выражения
где qsw – усилие в хомутах на единицу длины элемента, определяется по формуле: Для таких элементов значение
Конструктивные требования по армированию поперечными стержнями. Поперечная арматура в балочных и плитных конструкциях, устанавливается: - на приопорных участках длиной 1/4пролета (в зоне максимальной поперечной силы): при h ≤ 450 мм. . . . . . . . . . . . . . . . . . не более h/2 и не более 150 мм; при h > 450 мм. . . . . . . . . . . . . . . . . . не более h/3 и не более 500 мм; - на остальной части пролета. . . . . . . . . . . . не более 3h/4 и не более 500 мм. Расчет прочности по наклонным сечениям на действие поперечной силы элементов без поперечной арматуры. Прочность элемента по наклонному сечению на действие поперечной силы элементов без поперечной арматуры обеспечивается условием:
где правая часть условия принимается не более Коэффициент

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 превысят сопротивление бетона растяжению Rbt, возникают наклонные трещины. Растягивающие усилия в наклонной трещине передаются на арматуру. При дальнейшем увеличении нагрузки наклонные трещины раскрываются, напряжения в арматуре доходят до предела текучести и происходит разрушение элемента вследствие раздробления бетона над вершиной наклонной трещины (рис. 37).
превысят сопротивление бетона растяжению Rbt, возникают наклонные трещины. Растягивающие усилия в наклонной трещине передаются на арматуру. При дальнейшем увеличении нагрузки наклонные трещины раскрываются, напряжения в арматуре доходят до предела текучести и происходит разрушение элемента вследствие раздробления бетона над вершиной наклонной трещины (рис. 37).
 Экспериментально установлено, что прочность железобетонных элементов по наклонной полосе между наклонными трещинами обеспечена, если соблюдается условие:
Экспериментально установлено, что прочность железобетонных элементов по наклонной полосе между наклонными трещинами обеспечена, если соблюдается условие:
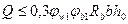 ,
, - коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, определяется по формуле:
- коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, определяется по формуле:  , где
, где  ,
,  ;
;  - определяется по формуле:
- определяется по формуле: 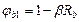 , где β – коэффициент, зависящий от вида бетона; Rb - в МПа.
, где β – коэффициент, зависящий от вида бетона; Rb - в МПа.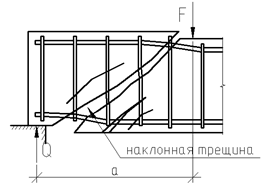
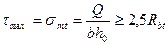 .
. Если касательные напряжения не достигают максимального значения, наклонные трещины не образуются.
Если касательные напряжения не достигают максимального значения, наклонные трещины не образуются. , поперечная арматура ставится конструктивно.
, поперечная арматура ставится конструктивно.
 Под воздействием изгибающего момента главные растягивающие напряжения начинают превышать сопротивление растяжению
Под воздействием изгибающего момента главные растягивающие напряжения начинают превышать сопротивление растяжению  , образуются наклонные трещины с максимальным раскрытием в растянутой зоне. Бетон растянутой зоны выключается из работы и все растягивающие усилия передаются на арматуру. Происходит взаимный поворот частей элемента относительно точки М (рис. 40). При слабом заанкеривании арматура выдергивается, при хорошем – сжатая зона бетона сокращается по высоте и разрушается.
, образуются наклонные трещины с максимальным раскрытием в растянутой зоне. Бетон растянутой зоны выключается из работы и все растягивающие усилия передаются на арматуру. Происходит взаимный поворот частей элемента относительно точки М (рис. 40). При слабом заанкеривании арматура выдергивается, при хорошем – сжатая зона бетона сокращается по высоте и разрушается.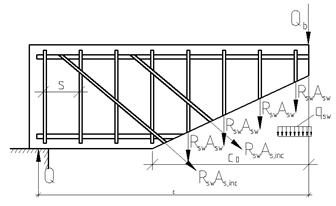
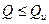 ;
;  ,
, где Q – поперечная сила от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения;
где Q – поперечная сила от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения;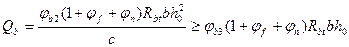 ,
,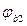 - коэффициент, учитывающий влияние вида бетона (для тяжелого бетона
- коэффициент, учитывающий влияние вида бетона (для тяжелого бетона 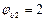 );
);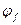 - коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах, определяется по формуле:
- коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах, определяется по формуле: 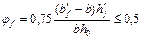 , где
, где 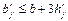 ;
;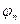 - коэффициент, учитывающий влияние продольных сил (учет влияния предварительно-напряженной арматуры), определяется по формуле:
- коэффициент, учитывающий влияние продольных сил (учет влияния предварительно-напряженной арматуры), определяется по формуле:  .
.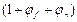 во всех случаях принимается не более 1,5.
во всех случаях принимается не более 1,5.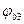 - коэффициент, учитывающий влияние вида бетона (для тяжелого бетона
- коэффициент, учитывающий влияние вида бетона (для тяжелого бетона  ).
). и
и 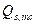 определяются как сумма проекций на нормаль к продольной оси элемента предельных усилий соответственно в хомутах и отгибах, пересекающих опасную наклонную трещину.
определяются как сумма проекций на нормаль к продольной оси элемента предельных усилий соответственно в хомутах и отгибах, пересекающих опасную наклонную трещину.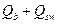 , определяемому по формуле:
, определяемому по формуле: .
.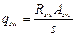 , при этом для хомутов, устанавливаемых по расчету, должно удовлетворяться условие:
, при этом для хомутов, устанавливаемых по расчету, должно удовлетворяться условие:  .
. ,
, ,
,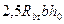 и не менее
и не менее 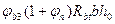 .
.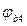 учитывает влияние вида бетона (для тяжелого бетона
учитывает влияние вида бетона (для тяжелого бетона  ).
).