
|
|
Метод непосредственного интегрированияПервообразная функции. Неопределенный интеграл
В дифференциальном исчислении решается задача: по данной функции Например, для функции Определение 1.1. Функция
или
Замечание. Понятие первообразной можно ввести и для других промежутков (отрезка, полуинтервала – конечного или бесконечного).
Например, для функции Но не только функция Сформулируем (без доказательства) основную теорему о первообразной. Теорема 1.1. Всякая непрерывная на интервале В данной теореме включены два утверждения. Рассмотрим их. 1) Выражение 2) Пусть
Определение 1.2. Совокупность всех первообразных функций
Здесь Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Правильность интегрирования всегда можно проверить дифференцированием результата. Заметим следующее: если производная от элементарной функции всегда является элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций. График первообразной от функции
параллельном движении одной из них по вертикали.
Свойства неопределенного интеграла
Отметим ряд свойств (без доказательства) неопределенного интеграла, вытекающих из его определения. Некоторые свойства мы докажем.
Свойство 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции.
Благодаря свойству 1 правильность интегрирования проверяется дифференцированием.
Свойство 2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
Свойство 3. Постоянный множитель можно выносить за знак интеграла:
Свойство 4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций:
Свойство 5 (инвариантность формулы интегрирования). Если
Пример 1.1. Найти интеграл Решение. ,
Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул дифференциального исчисления и использование свойств неопределенного интеграла. Интегралы в приводимой ниже таблице называются табличными. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения первообразных (т.е. интегрирования функций) сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы наизусть и уметь их узнавать.
Таблица основных интегралов
1. 2. 3. 4. 5 6. 7. 8. 9. 10.
Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Пример 1.2. Найти следующие интегралы: 1)
2)
3)
4)
,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 найти ее производную (или дифференциал). Теперь перейдем к изучению обратной задачи, которая имеет очень большое значение в анализе и его приложениях: найти функцию
найти ее производную (или дифференциал). Теперь перейдем к изучению обратной задачи, которая имеет очень большое значение в анализе и его приложениях: найти функцию  , зная ее производную (или дифференциал), т.е. выполняется условие
, зная ее производную (или дифференциал), т.е. выполняется условие  . Искомая функция
. Искомая функция  первообразной является функция
первообразной является функция  , т.к. выполняется условие
, т.к. выполняется условие 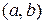 , если для любого
, если для любого  выполняется равенство
выполняется равенство .
. первообразной является функция
первообразной является функция  , так как
, так как 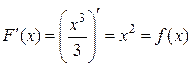 .
. является первообразной для функции
является первообразной для функции  . Функции
. Функции  ,
,  ,
,  тоже являются первообразными для функции
тоже являются первообразными для функции 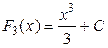 вместо
вместо  можно подставить любое действительное число. Таким образом, напрашивается следующий вывод: первообразных у данной функции не одна, а бесчисленное множество, так как постоянная величина
можно подставить любое действительное число. Таким образом, напрашивается следующий вывод: первообразных у данной функции не одна, а бесчисленное множество, так как постоянная величина 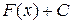 , где
, где  - произвольная постоянная, охватывает все без исключения первообразные для
- произвольная постоянная, охватывает все без исключения первообразные для 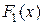 и
и 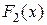 - две первообразные на интервале
- две первообразные на интервале  и
и  . Тогда
. Тогда  , где
, где  , т.е.
, т.е. (1.1)
(1.1)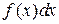 - подынтегральным выражением,
- подынтегральным выражением,  - переменной интегрирования, символ
- переменной интегрирования, символ  - знак неопределенного интеграла.
- знак неопределенного интеграла. . Очевидно, мы получим любую другую интегральную кривую, если пере-
. Очевидно, мы получим любую другую интегральную кривую, если пере-
 ,
,
 .
. .
. .
.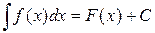 , то и
, то и  , где
, где  - произвольная функция, имеющая непрерывную производную.
- произвольная функция, имеющая непрерывную производную. .
. [по свойству 3]=
[по свойству 3]=  [по свойству 5]=
[по свойству 5]=  [по свойству 2]=
[по свойству 2]=  .
. ; 11.
; 11.  ;
;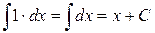 ; 12.
; 12. 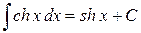 ;
; ; 13.
; 13.  ;
; ; 14.
; 14.  ;
; ; 15.
; 15.  ;
; ; 16.
; 16.  ;
;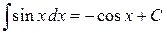 ; 17.
; 17.  ;
; ; 18.
; 18.  .
. ;
; ;
;
 ;
;
 ;
; ;
;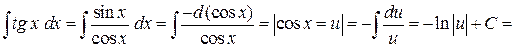
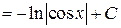 .
.