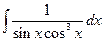|
|
Интегрирование трансцендентных функцийИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СПЕЦИАЛЬНЫХ ПОДСТАНОВОК
Теоретические вопросы 1. В каких случаях рационализация дифференциала достигается подстановкой cosx=t? Приведите доказательство. 2. В каких случаях рационализация дифференциала достигается подстановкой sinx=t? Приведите доказательство. 3. В каких случаях применяется подстановка 4. Дайте определение биномиального дифференциала. 5. Назовите универсальную подстановку, с помощью которой всегда достигается рационализация дифференциала вида 6. В каких случаях берется интеграл
7. Укажите подстановки Чебышева. 8. Что такое «интегральный логарифм», «интегральный синус» и «интегральный косинус»? 9. Записать универсальную тригонометрическую подстановку.
Практические задания Частные подстановки 1) Если функция 2) Если функция 3) Если функция Пример 1.Вычислить интеграл Решение.
Функция нечетная относительно
Можно было решить проще, а именно
Пример 2. Вычислить интеграл Решение. Функция
Пример 3. Вычислить интеграл Решение. Функция
Упражнения для самостоятельной работы 1. Вычислите интегралы.
Биномиальный интеграл Интеграл Как было показано П.Л. Чебышевым, интеграл от дифференциального бинома берется тогда и только тогда, когда хотя бы одно из чисел – если – если – если Пример 4. Вычислить интеграл Решение. Здесь
в последнем интеграле следует воспользоваться рекуррентной формулой для интегрирования рациональных выражений (формула 4), тогда
Выполняя подстановку, получим:
Пример 5. Вычислить интеграл Решение.
Распишем подынтегральное выражение на сумму
приравнивая числители, имеем систему
Решая систему, получаем
Вернемся к старой переменной, так как
Пример 6. Вычислить интеграл Решение. здесь
тогда
Вернемся к старой переменной, так как
Упражнения для самостоятельной работы 2. Вычислите интегралы.
Интегрирование трансцендентных функций Интегралы от трансцендентных функций часто можно свести к рациональному выражению с помощью так называемой универсальной подстановки
при этом
функции Пример 7. Вычислить интеграл Решение. Воспользуемся формулами (1), (2), (3), тогда
Распишем полученную дробь на три дроби:
возвращаясь к переменной х, получим
Замечание 1.Универсальная подстановка (1), (2), (3), приводит иногда к сложным выкладкам и пользоваться ею нужно лишь в крайнем случае, когда иных путей нет. Поэтому на практике, там, где это возможно, целесообразно прибегать к другим тригонометрическим приемам и подстановкам. Замечание 2.Многие интегралы от тригонометрических функций могут быть вычислены не только применением указанных выше подстановок, но и с помощью некоторых преобразований интегральной функции. Для этих преобразований нельзя дать никаких общих правил, а всякий раз индивидуальные особенности подынтегральной функции должны подсказать те преобразования, которые ведут к цели более простым и коротким путем. Замечание 3.При вычислении интеграла вида:
где k, m – натуральные числа, в числителе целесообразно вводить «тригонометрическую единицу» в подходящей степени. Замечание 4.При вычислении интегралов вида:
где k, m – натуральные числа, целесообразно выразить отношение одинаковых степеней синуса и косинуса через тангенс
Упражнения для самостоятельной работы 3. Вычислите интегралы:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  ?
?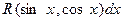 и покажите, как ею воспользоваться.
и покажите, как ею воспользоваться. ?
? нечетная относительно
нечетная относительно  , то есть
, то есть  , то применяется подстановка
, то применяется подстановка  ;
; , то есть
, то есть  , то применяется подстановка
, то применяется подстановка  ;
; , то применяется подстановка
, то применяется подстановка  или
или  .
. .
. ;
;  .
.

 .
. .
. .
. – нечетная относительно
– нечетная относительно 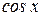 , тогда
, тогда
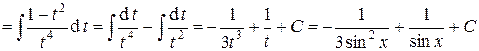 .
. .
. – четная относительно
– четная относительно 
 .
. ;
;
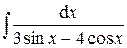 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 (
(  ,
,  ), числа
), числа  ,
,  и
и  – рациональные, а
– рациональные, а 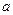 и
и  – вещественные.
– вещественные.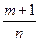 или
или  является целым:
является целым: , используется подстановка
, используется подстановка  , где
, где  – наименьшее общее кратное чисел
– наименьшее общее кратное чисел  , работает подстановка
, работает подстановка  , где
, где  – знаменатель дроби
– знаменатель дроби  ;
; ,
,  где
где 
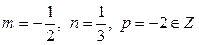 , поэтому используем подстановку
, поэтому используем подстановку  , тогда выполняя подстановку, имеем
, тогда выполняя подстановку, имеем

 .
.

 , здесь
, здесь  - имеем второй случай, поэтому используем подстановку
- имеем второй случай, поэтому используем подстановку  , тогда
, тогда 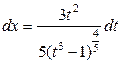 . Выполним полную замену в интеграле
. Выполним полную замену в интеграле
 ,
,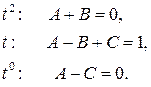
 , следовательно, возвращаясь к интегралу, имеем
, следовательно, возвращаясь к интегралу, имеем

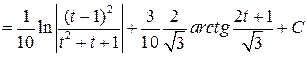 .
. то
то
 .
. ,
, - имеем третий случай, поэтому используем подстановку
- имеем третий случай, поэтому используем подстановку
 . Выполним полную замену в интеграле
. Выполним полную замену в интеграле
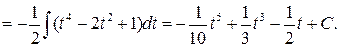
 , то
, то
 ;
;
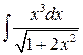 ;
;
 ;
;
 ;
;
 ;
;
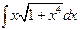 .
.



 , (1)
, (1)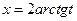 и
и  , (2)
, (2) также рационально выражаются через t:
также рационально выражаются через t: (3)
(3)
 . (4)
. (4)

 следовательно (4) примет вид
следовательно (4) примет вид ,
,
 ,
, ,
, 
 , (5)
, (5) и
и  , (6)
, (6) (7)
(7) ;
;
 ;
;
 ;
;
 ;
;
 ;
;