
|
|
Интегрирование простейших дробей четырех типовИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ
Теоретические вопросы 1. Дать определение многочлена. 2. Какое число называется корнем многочлена. 3. Что такое кратность корня. 4. Сформулируйте теорему о разложимости многочлена на множители. 5. В чем заключается характерная особенность класса рациональных функций. 6. Перечислите четыре типа простых дробей. 7. Сформулируйте теорему о разложимости дроби на сумму простых дробей. 8. Покажите, как вычисляются каждый из интегралов от простейших дробей? 9. В чем состоит применение метода неопределенных коэффициентов к разложению правильной дроби в сумму простых. 10. Запишите вывод интегралов от четырех основных рациональных дробей. 11. Перечислите этапы алгоритма вычисления интегралов от рациональной функции. Практические задания Самый важный класс функций, интегралы от которых всегда выражаются через элементарные функции, представляют рациональные функции, т. е. функции R(x), представимые в виде
где P(x) и Q(x) - многочлены с действительными коэффициентами. Если эта дробь неправильная, то ее представляем в виде:
где M(x)- многочлен, а Затем правильную остаточную дробь
В этом разложении знаменателя Q(x) множители первой степени соответствуют действительным корням, а множители второй степени - параммнимых сопряженных корней. Коэффициент при наибольшей степени x в знаменателе Q(x) можно считать равным единице, ибо этого всегда можно добиться, деля на него Р(x) и Q(x). Разумеется, если знаменатель Q(x) уже представлен в виде (1), корни искать излишне. После этого правильная остаточная дробь разлагается на простейшие по формуле
где Для нахождения неопределенных коэффициентов все простейшие дроби приводим к общему знаменателю Q(x) и приравниваем числители обеих частей равенства (2). Затем сравниваем коэффициенты при одинаковых степенях х. Это приводит к системе уравнений, из которых и находим значения интересующих нас коэффициенты. Наконец, находки интегралы выделенной целой части и всех простевших дробей, которые затем складываем. Интегрирование простейших дробей четырех типов А) Интегралы простейших дробей первого типа, то есть
непосредственно интегрируются. В). Интегралы простейших дробей второго типа берутся так:
(n>1-натуральное число). С). Интегралы простейших дробей третьего типа имеют вид:
В знаменателе подынтегральной функции выделяем полный квадрат
(A и B - некоторые числа), легко сводимое к табличным интегралам 2 и 8. Детали этого плана проследим на примере:
где Как и в предыдущем случае выделяем в знаменателе полный квадрат, подстановкой
где первый интеграл приводится к табличному 1, а второй - находится с помощью рекуррентной формулы. Пример 1. Вычислим Решение. Дискриминант в знаменателе меньше нуля:
Следовательно, интегрируется простейшая дробь третьего типа. Выделяем полный квадрат:
Следует заметить, что прием «выделения полного квадрата» должен стать привычным инструментом студентов. Тогда
где Пример 2. Вычислим интеграл Решение. Так как
тогда
Пример 3. Вычислим интеграл
Решение. Так как подынтегральная функция является неправильной дробью, то вначале выделяем целую часть Тогда подынтегральное выражение можно представить в виде суммы, а знаменатель разложим на множители
Воспользуемся теоремой. Теорема: Пусть
Теперь разложим дробь на сумму дробей
Найдем А, В, С для этого приведем к общему знаменателю правую часть
приравниваем числители
тогда два многочлена одной степени равны, если равны коэффициенты при одинаковых степенях независимой переменной х
Вернемся к интегралу (3) и распишем его в виде суммы дробей с найденными коэффициентами
Возвращаясь к исходному интегралу и используя свойства логарифмической функции, получим
или
Замечание. Прием, которым были найдены коэффициенты Для определения коэффициентов можно применять способ частных значений, состоящий в следующем: аргументу Вернемся к рассмотренному случаю. Из (4) получим:
Те же самые значения коэффициентов получены проще. Замечание. При поиске неизвестных коэффициентов рекомендуется комбинировать оба этих метода. 2) Знаменатель можно разложить лишь на множители первой степени, среди которых есть повторяющиеся. Пример 4. Вычислить интеграл Решение. Подынтегральная дробь правильная, поэтому разложение подынтегральной функции на простейшие дроби будет иметь вид:
Приведем правую часть к общему знаменателю, приравняем числители, получим:
3) Знаменатель можно разложить на неповторяющиеся множители второй степени и, может быть, множители первой степени. Пример 5. Вычислить интеграл Решение. Подынтегральная функция может быть разложена на простейшие дроби следующим образом:
Действуем аналогично предыдущим примерам.
Отсюда
Задание 1. Вычислить интегралы: 1.1 1.5 1.9 1.13 Ответы 1.2 1.4 1.6 1.8 1.10 1.12 1.14 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
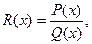

 - остаток от деления P(x) наQ(x).
- остаток от деления P(x) наQ(x). разлагаем на простейшие дроби. Для этого находим корни уравнения Q(x)=0 и разлагаем знаменатель на множители первой и второй степени с действительными коэффициентами:
разлагаем на простейшие дроби. Для этого находим корни уравнения Q(x)=0 и разлагаем знаменатель на множители первой и второй степени с действительными коэффициентами: . (1)
. (1)
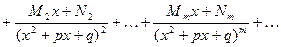 , (2)
, (2)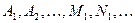 - неопределенные (неизвестные) коэффициенты (некоторые из них могут равняться нулю).
- неопределенные (неизвестные) коэффициенты (некоторые из них могут равняться нулю).
 ,
, , где
, где  .
. а затем подстановкой
а затем подстановкой  приводим интеграл к виду:
приводим интеграл к виду: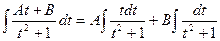


 ,
,  .
. приводим интеграл к виду
приводим интеграл к виду ,
, .
. .
. .
.
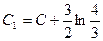 .
.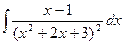 .
. , то интегрируется простейшая дробь четвертого типа. Следовательно,
, то интегрируется простейшая дробь четвертого типа. Следовательно,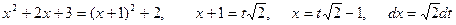 ,
,
 .
.
 (3)
(3)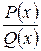 – правильная рациональная дробь,
– правильная рациональная дробь,  и
и 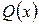 – многочлены с действительными коэффициентами. Если
– многочлены с действительными коэффициентами. Если ,
, – попарно различные действительные корни многочлена
– попарно различные действительные корни многочлена 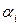 ,
,  ,
,  ,
, 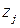 и
и  – попарно различные при разных
– попарно различные при разных  существенно комплексные корни многочлена
существенно комплексные корни многочлена  ,
,  , то существуют действительные числа
, то существуют действительные числа  ,
,  ,
,  и
и  ,
,  , такие что
, такие что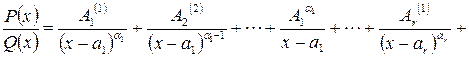




 , (4)
, (4)

 .
.
 ,
,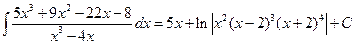 .
. , называется способом сравнения коэффициентов.
, называется способом сравнения коэффициентов. придают некоторые «удобные» значения (ими могут быть значения корней).
придают некоторые «удобные» значения (ими могут быть значения корней).
 .
. .
. ,
, .
.
 , тогда
, тогда 

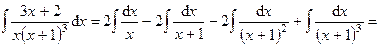
 .
. .
. .
. ,
,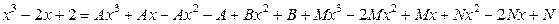 .
.
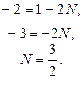
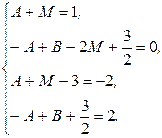


 . Тогда
. Тогда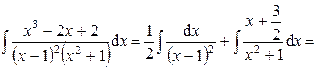
 .
. 1.2
1.2  1.3
1.3  1.4
1.4 
 1.6
1.6  1.7
1.7  1.8
1.8 
 1.10
1.10  1.11
1.11 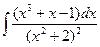 1.12
1.12 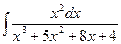
 1.14
1.14  1.15
1.15  1.16
1.16  .
. ; 1.3
; 1.3  ;
;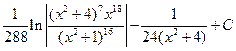 ; 1.5
; 1.5  ;
; ; 1.7
; 1.7  ;
; ; 1.9
; 1.9 
 ; 1.11
; 1.11 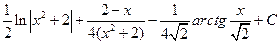
 ; 1.13
; 1.13  ;
; ; 1.15
; 1.15  .
.