
|
|
Метод непосредственного интегрирования12 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Перед изучением темы целесообразно повторить известные из раздела “Дифференциальное исчисление функции одной переменной” понятия производной и дифференциала функции, таблицы производных и дифференциалов, а также технику вычисления производных. Теоретические вопросы 1. Дайте определение первообразной функции и интеграла от заданной функции 2. Какова общая формула записи всех первообразных от заданной функции 3. Что называется неопределенным интегралом от 4. Сформулируйте свойства неопределенного интеграла, непосредственно вытекающие из его определения. 5. В чем разница между выражениями: 6. Запишите таблицу основных интегралов. Покажите, как каждая из ее формул получается из соответствующей формулы для производной. 7. Докажите, что 8. Чему равен неопределенный интеграл от суммы дифференциалов? 9. Чему равен интеграл 10. На каком свойстве дифференциала основан метод замены переменной или подстановки? 11. При каких условиях применим метод замены переменной? 12. Чему равен интеграл 13. Покажите, что правило интегрирования по частям есть следствие правила дифференцирования произведения функций. 14. Назовите классы интегралов, которые можно вычислить интегрированием по частям. 15. В чем особенности вычисления интегралов: 16. Выведите рекуррентную формулу для вычисления интеграла 17. Приведите примеры интегралов, не выражающихся в конечном виде через элементарные функции.
Практические задания
Отыскание неопределенного интеграла некоторой функции называется интегрированием. Интегрирование представляет собой операцию, обратную дифференцированию, поэтому каждой формуле дифференцирования соответствует формула интегрирования Следует заметить, что термин "первообразная" функция, как же термин "производная" функция введен французским математиком Лагранжем. Как вы убедились при изучении предыдущего раздела "Дифференциальное исчисление функции одной переменной" производная от любой элементарной функции есть обязательно функция элементарная, которая легко вычисляется по известным вам правилам. Первообразная же от любой элементарной функции хотя всегда и существует, но во многих случаях не является элементарной, а представляет собой новую трансцендентную функцию. Существует три основных метода отыскания неопределенных интегралов: 1) метод непосредственного интегрирования, 2) метод замены переменной, 3) метод интегрирования по частям. Остановимся на каждом из них. Метод непосредственного интегрирования Он опирается на таблицу основных интегралов и простейшие правила интегрирования. Функция Общее выражение
Свойства неопределенного интеграла. I. II. III. т.е. постоянный множитель можно выносить за знак интеграла. IV. т. е. интеграл от суммы равен сумме интегралов от всех слагаемых. Таблица основных интегралов
10. 11. Следует заметить, что все эти формулы справедливы независимо от того, является ли u независимой переменной либо какой угодно функцией независимой переменной. Простейшие правила интегрирования 1. 2. 3. Если Очень часто встречаются случаи, когда а=1 либо b=0. Вспомним таблицу дифференциалов и запишем ее в следующем виде: 1. 3. 5. 7. 9. 11. Примечание 1. Вообще
Этой таблицей мы будем широко пользоваться и представление Например, Поскольку интегрирование – обратное действие по отношению к дифференцированию, то благодаря этому проверка результата интегрирования может осуществляться дифференцированием его. Полученная производная должна совпадать с подынтегральной функцией. Непосредственным интегрированием будем называть интегрирование с помощью таблицы основных интегралов, простейших правил интегрирования и тождественных преобразований подынтегральной функции. Пример 1. Вычислим интегралы: 1. 3. 5. 7. Решение. 1. Записываем подынтегральную функцию в виде степени с отрицательным дробным показателем и применяем формулу 1 из таблицы основных интегралов:
Замечание 1. Если подынтегральное выражение можно преобразовать к виду произведения степени
2. Числитель подынтегральной функции делим почленно на знаменатель. Затем применяя правила 2. 1 и формулу 1 из таблицы основных интегралов:
Замечание 2. В примере 2 и далее произвольные постоянные, входящие, по определению, в каждый из складываемых неопределенных интегралов, объединяем в одну произвольную постоянную. 3. Возводим числитель в квадрат, делим почленно числитель на знаменатель и далее поступаем как в примере 2.
4. Сначала исключаем целую часть рациональной дроби, деля числитель на знаменатель. Имеем:
Применяя правило 2, получаем:
Первые три интеграла правой части вычисляются по правилу 1 и формуле 1из таблицы, а к последнему интегралу применяем правило 3 интегрирования при
Замечание 3. Последний интеграл можно было вычислить используя формулы 1 и 3 из таблицы дифференциалов:
Другими словами, функцию Замечание 4. Если подынтегральная функция представляет собой рациональную дробь, у которой степень многочлена числителя больше или равна степени знаменателя, то, прежде всего, следует выделить целую часть путем деления числителя рациональной дроби на знаменатель. 5. Чтобы свести данный интеграл к табличному, достаточно прибавить и вычесть в числителе подынтегральной функции
Следует заметить, что примененные здесь прием добавления в числителе подынтегральной функция взаимно уничтожающихся слагаемые иногда бывает полезен. 6. Для нахождения интеграла применяем правило 1, а затем заменяем единицу в числителе подынтегральной функции выражением
7. Освободимся в знаменателе от иррациональности, воспользуемся правилами 2 к 3 интегрирования и формулой 1 и 5 таблицы основных интегралов:
8. Чтобы свести данные интеграл к табличному, достаточно подвести под знак дифференциала множитель
3амечание 5. Совершенно аналогично вычисляются интегралы вида
Необходимо в каждом из них ввести под знак дифференциала множитель b разделить интеграл на этот множитель. Тогда получаем табличные интегралы соответственно 10 и 9 или 11, причем u=bx. Замечание 6 Метод непосредственного интегрирования дает возможность вычислять интегралы вида Действительно, так как
Здесь положили u=f(x). Итак, если числитель подынтегральной функции равен производной ее знаменателя, то интеграл равен логарифму модуля знаменателя плюс произвольная постоянная. Рассмотрим примеры. Пример 2. Найдем интеграл Решение. Пример 3. Вычислим интеграл Решение.
Задание 1. Вычислить интегралы 1.1 1.3. 1.5. 1.7. 1.9. 1.11. 1.13. 1.15. 1.17. 1.19. 1.21. 1.23. 1.25. 1.27. 1.29. 1.31. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 на заданном промежутке.
на заданном промежутке. и
и  ?
?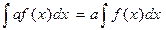 , где a – постоянная, не равная нулю.
, где a – постоянная, не равная нулю. , если известно, что
, если известно, что  ?
? .
. ,
,  ?
? ,
, 
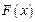 называется первообразной функцией от функции
называется первообразной функцией от функции  , если она удовлетворяет условию
, если она удовлетворяет условию  .
. совокупности всех первообразных от функции
совокупности всех первообразных от функции  , если
, если 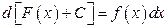 .
. или
или  .
. или
или 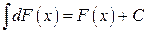 .
. ,
, ,
,
 ,
, ,
, ,
,  ,
,
 ,
,
 ,
, ,
,




 , где
, где 
 .
. .
. то
то  , где
, где  2.
2.  ,
,  .
. . 4.
. 4.  .
. . 6.
. 6.  .
. . 8.
. 8.  .
. . 10.
. 10.  .
. .
.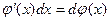 .
. в виде
в виде  мы будем называть «подведением функции
мы будем называть «подведением функции  под знак дифференциала».
под знак дифференциала». . Функцию
. Функцию  подвели под знак дифференциала.
подвели под знак дифференциала. . 2.
. 2.  .
. . 4.
. 4. 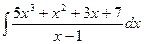 .
. . 6.
. 6.  .
. . 8.
. 8.  .
. .
.
 на дифференциал основания
на дифференциал основания  , то интеграл вычисляется по формуле
, то интеграл вычисляется по формуле

 .
.
 .
. .
.
 и
и  и формулу 2 из таблицы основных интегралов:
и формулу 2 из таблицы основных интегралов: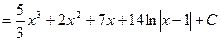 .
. .
. подвели под знак дифференциала и получили табличный интеграл.
подвели под знак дифференциала и получили табличный интеграл. получаем:
получаем: .
. и используем формулы 6 и 7 таблицы основных интегралов:
и используем формулы 6 и 7 таблицы основных интегралов: .
.
 и разделить весь интеграл на
и разделить весь интеграл на  ,
,  .
. .
. ,
,  ,
,  .
. .
. (см. примечание 1) , то
(см. примечание 1) , то .
.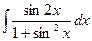 .
. .
. .
.
 . 1.2.
. 1.2.  .
. . 1.4.
. 1.4. 
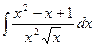 . 1.6.
. 1.6.  .
. . 1.8.
. 1.8.  .
. . 1.10.
. 1.10.  .
. . 1.12.
. 1.12.  .
. . 1.14.
. 1.14.  .
. . 1.16.
. 1.16.  .
. . 1.18.
. 1.18.  .
.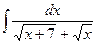 . 1.20.
. 1.20. 
 . 1.22.
. 1.22. 
 . 1.24.
. 1.24. 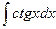 .
. . 1.26.
. 1.26.  .
. . 1.28.
. 1.28.  .
. . 1.30.
. 1.30.  .
.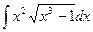 . 1.32.
. 1.32.  .
.