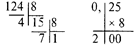Перевод дробных чисел из системы счисления

Перевод правильных дробей

Пусть А_др — десятичная дробь, тогда в ее разложении отсутствуют коэффициенты с положительными индексами:

Таким образом, необходимо найти коэффициенты а_–1, а_–2, ... , входящие в запись числа в двоичной системе счисления.

Умножим правую и левую части выражения (3) на 2. В результате в правой части получим: a_–1 + a_–2 × 2^–1 + a_–3×2^–2+ ...

Целая часть и даст нам старший коэффициент в разложении числа А_др по степеням двойки.

Оставшуюся дробную часть умножим на 2: а_–2 + а_–3× 2^–1+ ...

Цифра а_–2 представляет собой второй коэффициент после запятой в двоичном представлении исходного числа.

Описанный процесс необходимо продолжать до тех пор, пока в правой части не получим нуль или пока не будет достигнута необходимая точность вычислений.

Пример 3. Перевести десятичную дробь 0,5625 в двоичную систему счисления. Вычисления лучше всего оформлять по следующей схеме:

Пример 4. Перевести в двоичную систему счисления десятичную дробь 0,7.

Очевидно, что этот процесс может продолжаться бесконечно, давая все новые и новые знаки в изображении двоичного эквивалента числа 0,7₁₀. Так, за четыре шага мы получаем число 0,1011₂, а за семь шагов — число 0,1011001₂, которое является более точным представлением числа 0,7₁₀ в двоичной системе счисления, и т. д. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа.

Перевод смешанных чисел

Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой). См. подразд. 2.3.

Пример 5. Перевести число 17,25 в двоичную систему счисления.

Переводим целую часть: Переводим дробную часть:

Ответ:17,25₁₀=10001,01₂.

Перевод целых чисел из системы счисления

с основанием р в систему счисления с основанием q

По аналогии с рассмотренными алгоритмами можно сформулировать алгоритм перевода целых чисел из системы счисления с основанием р в систему счисления с основанием q:

Перевод дробных чисел из системы счисления

с основанием р в систему счисления с основанием q

Можно сформулировать следующий алгоритм правило перевода правильной дроби из системы счисления с основанием р в систему счисления с основанием q:

1) основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления;

2) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или пока не будет достигнута требуемая точность представления числа;

3) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления,

4) привести в соответствие с алфавитом новой системы счисления;

5) составить дробную часть числа в новой системе счисления начиная с целой части первого произведения.

Пример 1. Перевести число 0,65625₁₀ в восьмеричную систему счисления.

0,
	*8
	*8

Ответ: 0,65625₁₀ = 0,52₈.

Пример 2. Перевести число 0,65625₁₀ в шестнадцатеричную систему счисления.

0,
	*16
(A)	*16

 

 

Ответ: 0,65625₁₀ = 0,А8₁₆.

Пример 3. При переводе смешанных чисел отдельно переводятся целые и дробные части. Перевести число 124,25₁₀ в восьмеричную систему.

 

Ответ: 174,2₈

 

 

12

---

Не нашли, что искали? Воспользуйтесь поиском по сайту:

©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.