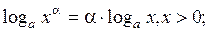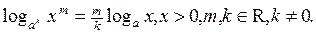|
|
Метод интегрирования подстановкой (замена переменной).МЕТОДЫ ИНТЕГРИРОВАНИЯ
Методические указания к решению задач по теме «Методы интегрирования» для студентов ФАВТ, ФМА, ФФиТРМ дневного, вечернего и заочного отделений САНКТ-ПЕТЕРБУРГ
Составители: Н.И. Васильева, Е.Ю. Непомнящая
Рецензент: Е.Н. Бегун
Утверждено на заседании кафедры математики и информатики. Протокол №8 от 9 января 2012 года.
Данные методические указания предназначены для самостоятельного изучения раздела высшей математики "Неопределенный интеграл" и содержат теоретические сведения и примеры решения задач по технике интегрирования. Первообразная и неопределенный интеграл. Определение 1. Функция
Пример. Функция Функция Мы видим, что две первообразные для одной и той же функции отличаются только постоянной. Очевидно, что если Определение 2. Совокупность всех первообразных
где Примеры. 1. 2. Понятно, что проверку нужно сделать дифференцированием. Сделайте это самостоятельно.
Свойства неопределенного интеграла. 1. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная от неопределенного интеграла равна подынтегральной функции:
3. Постоянный множитель можно выносить за знак интеграла
4. Неопределенный интеграл от суммы двух или конечного числа функций равен сумме интегралов от этих функций:
5. где Инвариантность формулы интегрирования Если Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или функцией от нее. Операция нахождения неопределенного интеграла называется интегрированием. Запишем ряд интегралов, которые в дальнейшем будем считать табличными. Таблица 1 1. 2. 2а. 2b. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. Формулы 2a и 2b являются частными случаями формулы 2 при В таблице аргумент подынтегральной функции обозначен через t, при этом аргумент может быть как независимой переменной, так и функцией. В дальнейшем под термином "интеграл" мы будем понимать «неопределенный интеграл».
Вычисление интегралов с помощью таблицы интегралов и их свойств Рассмотрим несколько интегралов, которые могут быть получены с использованием таблицы интегралов, свойств интегралов (§1) и преобразований подынтегральной функции. 1. Найти Решение. Используя формулу
2. Найти Решение. Преобразуем подынтегральную функцию: проведем почленное деление и преобразование степеней.
Здесь мы использовали свойства 3, 4, а также табличные интегралы 2,3. 3. Найти Решение.
4. Найти Решение. Используя свойство 5 и табличный интеграл 5, получаем
5. Найти Решение. Для удобства вынесем знак минус за знак интеграла (свойство 3):
Самостоятельно определите, какое свойство и какой табличный интеграл были использованы. 6. Найти Решение.
7. Найти Подынтегральную функцию преобразуем в сумму (см. Приложение).
8. Найти Преобразуем подынтегральную функцию, используя формулу понижения степени (см. Приложение)
9. Найти Преобразуем подынтегральную функцию.
Задачи для самостоятельного решения.
Интегрирование методом подведения Под знак дифференциала Метод интегрирования «подведением под знак дифференциала» основан на свойстве инвариантности интеграла. Таблицу интегралов можно переписать следующим образом: Таблица 2 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Основная формула, которую мы используем в этом параграфе, следующая:
Запишем таблицу подведения под знак дифференциала. Она похожа и на таблицу производных (дифференциалов) и на таблицу интегралов. Помним, что операция подведения под знак дифференциала есть операция интегрирования, так как под дифференциалом оказывается первообразная для функции, находящейся в левой части формулы перед dx. Таблица 3
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Примеры применения формулы 1 были разобраны в §2. Обратимся к другим формулам. 1. Найти Применим формулу 5 из таблицы 3: Тогда Используя свойство инвариантности где
Легко проверить дифференцированием, что интеграл найден верно:
2. Найти Решение. Применим формулу 8 таблицы 3 и табличный интеграл 2 таблицы 2:
3. Найти Решение. Воспользуемся формулой 6 из таблицы 3.
4. Найти Решение. Воспользуемся формулой 3 из таблицы 3 и табличным интегралом 3 из таблицы 2.
5. Найти Здесь нам придется применить подведение под дифференциал дважды. Сначала воспользуемся формулой 1 таблицы 3:
Теперь воспользуемся формулой 3 таблицы 3 и табличным интегралом 7 таблицы 2:
6. Найти Решение. Сначала воспользуемся формулой 4 из таблицы 3, а затем формулой 9 таблицы 3 и табличным интегралом 2 таблицы 2:
7. Найти Решение. Под дифференциалом нужно получить выражение
Примеры для самостоятельного решения
Интегрирование по частям Формула интегрирования по частям
где u, v – дифференцируемые функции. Применение формулы целесообразно, если интеграл В качестве u выбирается функция, которая упрощается в результате дифференцирования, а в качестве Для некоторых интегралов можно дать общие рекомендации при интегрировании по частям. Эти рекомендации представим в виде таблиц.
Таблица 4
Примеры. 1 Найти Решение. Пользуясь рекомендацией таблицы 4, выберем
Заметим, что при нахождении
Итак, мы получили более простой интеграл
В дальнейшем для удобства и наглядности будем оформлять запись подстановок определенным образом. Рассмотренный пример выглядит так:
1. Найти Решение. Пользуясь таблицей 4, выберем
3. Найти Решение.
Обратите внимание на то, что в этом примере интегрирование по частям применено дважды. Причем, на первом этапе было видно, что мы на правильном пути, так как, понизив степень многочлена, мы уже упростили интеграл. 3. Найти Решение. Для этого интеграла нет рекомендаций в таблице 4.
Мы не получили интеграл проще, а получили подобный. Применим формулу интегрирования по частям еще раз:
В правой части мы получили исходный интеграл. Перенесем его в левую часть:
Следовательно,
Осталось добавить произвольную постоянную. Окончательно имеем
Интегралы такого типа называются «возвратными», так как в процессе преобразований мы возвращаемся к исходному интегралу. 4. Найти Решение.
5. Найти Решение.
Примеры для самостоятельного решения.
Метод интегрирования подстановкой (замена переменной).
Часто интеграл можно значительно упростить, сделав замену переменной. Такой метод интегрирования заключается в том, что при помощи подстановки переменная интегрирования заменяется на функцию от другой независимой переменной. Пусть нужно найти Сделаем замену переменной Получим формулу интегрирования подстановкой:
Эта формула также называется формулой замены переменной в неопределенном интеграле. После вычисления интеграла правой части формулы следует вернуться к старой переменной интегрирования x. Иногда бывает удобнее сделать подстановку в виде Примеры. 1. Найти Решение. Сделаем замену Тогда
Возвращаясь к переменной x, получаем
Можно использовать краткую запись, выделяя замену переменной и выкладки, связанные с ней, вертикальными линиями. Запись данного примера будет выглядеть так:
2. Вывести формулу для табличного интеграла Решение. Введем новую переменную Такая подстановка называется подстановкой Л. Эйлера. Выразим переменную x через t. Для этого проделаем следующие выкладки:
Найдем dx: Выразим
Подставим dx и
Замечание. Так как этот интеграл часто встречается в приложениях, а нахождение его трудоемко, мы включили его в основную таблицу интегралов. 3. Найти Решение. Сделаем замену
Теперь нужно вернуться к старой переменной. Получим
4. Решим предыдущий пример другим способом. Сделаем замену Применяя тригонометрическую формулу
получим
Следовательно,
Мы видим, что при различных подстановках получены разные по виду результаты. На самом деле можно доказать, что результаты одинаковы. 1. Найти Решение. Выделим в знаменателе полный квадрат
и сделаем замену
Примеры для самостоятельного решения
Приложение
Алгебраические выражения
Cвойства степеней
Логарифмы (

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 называется первообразной функции
называется первообразной функции  на интервале
на интервале 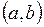 , если для любого
, если для любого  выполняется равенство
выполняется равенство
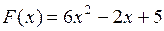 является первообразной для функции
является первообразной для функции 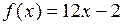 , так как
, так как  .
. также является первообразной для функции
также является первообразной для функции  содержит все первообразные функции
содержит все первообразные функции  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом  , то есть
, то есть
 ,
,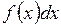 – подынтегральным выражением, а С – произвольной постоянной интегрирования.
– подынтегральным выражением, а С – произвольной постоянной интегрирования. , так как
, так как  .
.
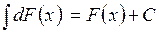
 ,
, .
.

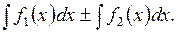

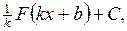

 , то и
, то и  , где
, где  – произвольная функция, имеющая непрерывную производную.
– произвольная функция, имеющая непрерывную производную.
 .
. 








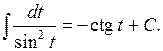
 .
.


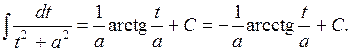



 и
и 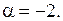

 сведем интеграл к табличному (формула 2):
сведем интеграл к табличному (формула 2):






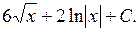





 .
. .
.

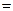










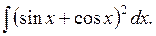
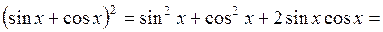









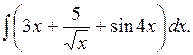





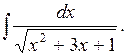





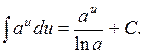




















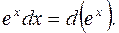

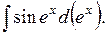
 и табличный интеграл
и табличный интеграл  получим
получим
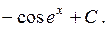

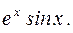









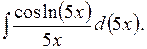



 .
.
 где a – любое число.
где a – любое число. Для этого используем формулы 1 и 2 из таблицы 3 и 2а таблицы 2.
Для этого используем формулы 1 и 2 из таблицы 3 и 2а таблицы 2.


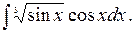


 (Рекомендуется внести в таблицу)
(Рекомендуется внести в таблицу)

 (Рекомендуется внести в таблицу)
(Рекомендуется внести в таблицу)






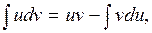
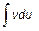 проще исходного интеграла или подобен ему.
проще исходного интеграла или подобен ему.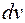 – оставшаяся часть подынтегрального выражения, из которой интегрированием можно найти
– оставшаяся часть подынтегрального выражения, из которой интегрированием можно найти  . При этом
. При этом 



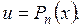





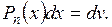





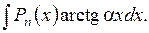
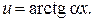


 – многочлен от x степени n.
– многочлен от x степени n. .
. ,
,  Далее следует найти du и v.
Далее следует найти du и v.
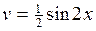 , так как
, так как 

 Найдя его и добавив постоянную C, получаем все семейство первообразных и окончательный ответ:
Найдя его и добавив постоянную C, получаем все семейство первообразных и окончательный ответ:
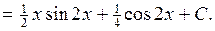
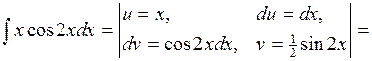
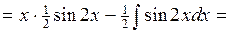
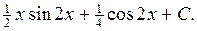
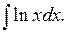
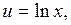
 . Получим
. Получим








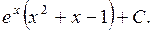

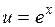 ,
, 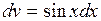 ,
,  ,
, 


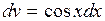 ,
, 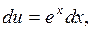

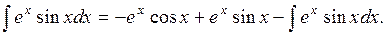



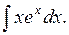

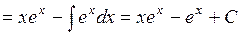 .
.
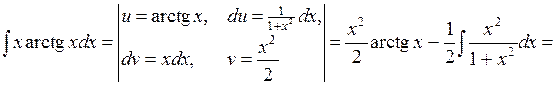
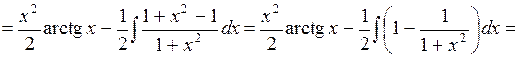









 .
.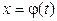 , где
, где  – функция, имеющая непрерывную производную. Тогда
– функция, имеющая непрерывную производную. Тогда  .
. .
. . Как это сделать мы увидим далее в процессе решения примеров.
. Как это сделать мы увидим далее в процессе решения примеров.


 , и
, и








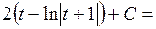









 через t:
через t:




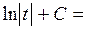


 . Тогда
. Тогда  ,
,  .
.


 . Тогда
. Тогда 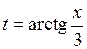 и
и 


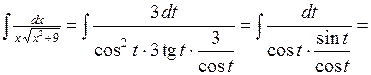
 .
.

 тогда
тогда






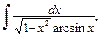











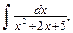








 ;
;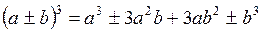 ;
;




 )
) ,
,