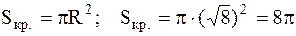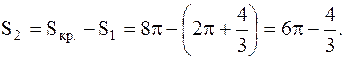|
|
Определение и свойства определенного интеграла12
Пусть на сегменте [a,b] задана функция f(x). Выполним следующие операции: 1. С помощью точек деления 2. На каждом малом сегменте выберем произвольную точку 3. Составим, так называемую, интегральную сумму всех таких произведений
Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма Таким образом, Числа а и b называются соответственно нижним и верхним пределами (границами) интегрирования, f(x) - подынтегральной функцией, а интервал [a,b] - областью интегрирования. Функция f(x), для которой существует конечный В теореме существования определенного интеграла указывается на то, что всякая непрерывная на промежутке [a,b] функция f(x) является интегрируемой на нем. Впредь подынтегральную функцию будем считать непрерывной. Без подробных объяснений приведем некоторые свойства определенных интегралов. 1. 2. 3. 4. Если 5. Если а) б) 6. Теорема о среднем:
7. 8.
Методы вычисления определенного интеграла
Вычисление определенных интегралов как пределов интегральных сумм связано в большими трудностями даже в тех случаях, когда подынтегральные функции являются простыми. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов. Ниже будет сформулирована теорема Ньютона-Лейбница, позволяющая сводить вычисления определенного интеграла к неопределенному. Эта теорема играет фундаментальную роль в математическом анализе.
Теорема Ньютона-Лейбница
Пусть f(x) непрерывна на сегменте [a,b] и F(x) - одна из ее первообразных, тогда справедлива формула
Пример 22. Вычислить Решение. Используя формулу Ньютона-Лейбница, а также табличный интеграл 16, получим
Пример 23. Вычислить Решение. Пусть Если Следовательно,
Формула интегрирования по частям в определенном интеграле
Пусть
Пример 24. Вычислить интеграл Решение. Применим полученную формулу
Приложения определенного интеграла. Вычисление площади плоской фигуры. Если задана непрерывная функция
(4.1)
Пусть криволинейная трапеция с основанием [a,b] ограничена снизу кривой
(4.2)
В некоторых случаях, чтобы вычислить площадь искомой фигуры, необходимо разбить ее на сумму или разность двух или более криволинейных трапеций и применить формулы (4.1) или (4.2) (рис.4.3. и 4.4)
Пример 25. Вычислить площадь фигуры, ограниченной линиями Решение.
Если
Найдем абсциссы точек пересечения прямой и параболы:
Для вычисления площади заштрихованной области воспользуемся формулой (4.4)
Решение. Сделаем чертеж (рис.4.6)
в начале координат и радиусом
в т.О(0,0) Найдем точки пересечения параболы и окружности:
Если Найдем площадь заштрихованной области по формуле (4.4), в которой изменены переменные интегрирования:
Найдем площадь второй (незаштрихованной) части, на которую круг разделен параболой
Список рекомендуемой литературы 1. Лунгу К.Н., Макаров Е.В. Высшая математика. Руководство к решению задач. - М.: ФИЗМАТЛИТ, 2005. 216с. 2. Пискунов Н.С. Дифференциальное и интегральное исчисления. ТТ.1- 2, М.: Интеграл-Пресс, 2001,2002. - 416с., 544с. 3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. ЧЧ. 1-2. - М.: Высшая школа, 1980-2000. - 304с., 416с. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
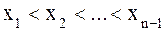 разобьем [a,b] на n малых сегментов:
разобьем [a,b] на n малых сегментов: 
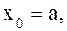
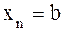 .
. ,
, 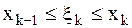 , составим произведение
, составим произведение 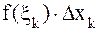 .
.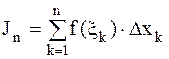 .
. , когда
, когда 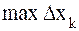 стремится к нулю.
стремится к нулю.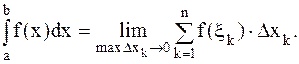
 , называется интегрируемой на промежутке [a,b], причем указанный предел не зависит ни от способа разбиения сегмента [a,b] на части, ни от выбора точек
, называется интегрируемой на промежутке [a,b], причем указанный предел не зависит ни от способа разбиения сегмента [a,b] на части, ни от выбора точек 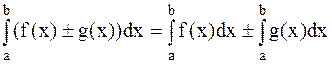 .
.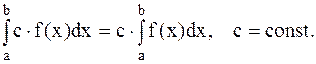
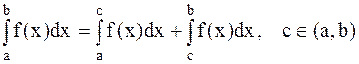 .
.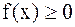 на [a,b], то
на [a,b], то 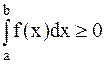 .
.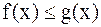 для
для  , то
, то
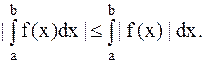
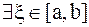 ,
,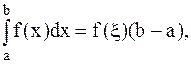 где
где 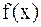 - непрерывна на [a,b].
- непрерывна на [a,b].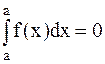 .
.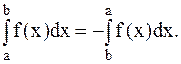
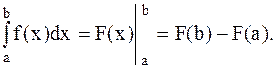
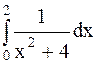 .
.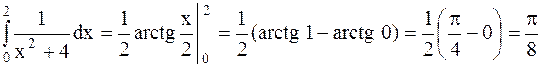 .
. .
.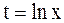 , тогда
, тогда 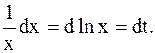
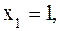 то
то 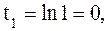 если
если 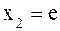 , то
, то 

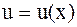 и
и 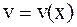 - непрерывные функции вместе со своими первыми производными на [a,b], тогда справедлива формула интегрирования по частям:
- непрерывные функции вместе со своими первыми производными на [a,b], тогда справедлива формула интегрирования по частям: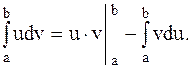
 .
.
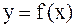 на [a,b],
на [a,b], 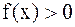 , то определенный интеграл с геометрической точки зрения представляет собой площадь так называемой, криволинейной трапеции (рис.4.1).
, то определенный интеграл с геометрической точки зрения представляет собой площадь так называемой, криволинейной трапеции (рис.4.1).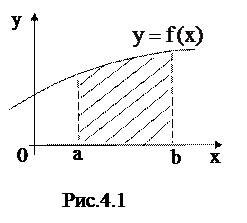
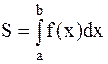
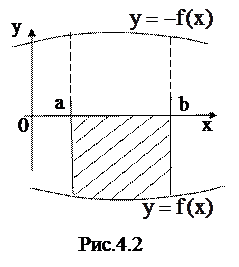

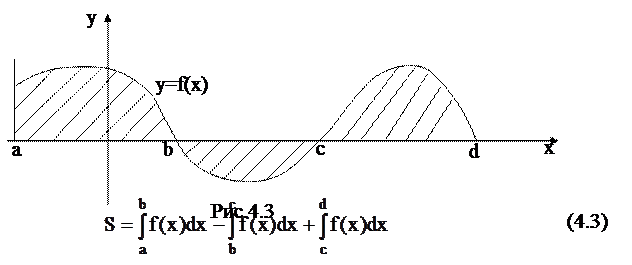

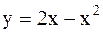 и
и 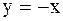 .
.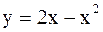 - парабола. Найдем ее вершину и точки пересечения с осями координат.
- парабола. Найдем ее вершину и точки пересечения с осями координат.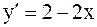 ;
; 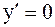 или
или 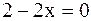 ,
, 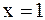
 , то
, то 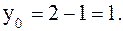
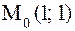 - вершина параболы.
- вершина параболы. или
или  или
или 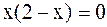
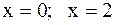 .
.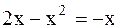 или
или 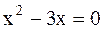
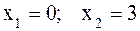 .
.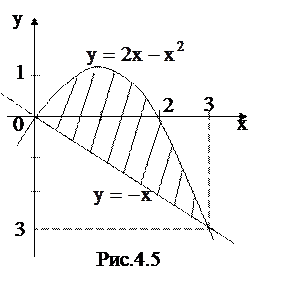
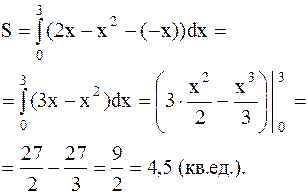
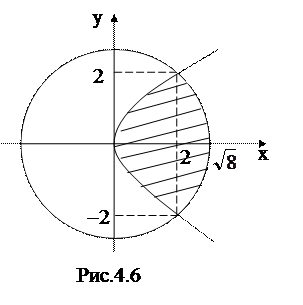 Пример 26. Вычислить площадь двух частей, на которые круг
Пример 26. Вычислить площадь двух частей, на которые круг 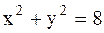 разделен параболой
разделен параболой 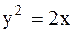 .
.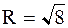 .
.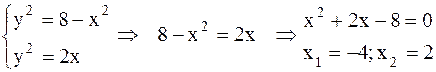
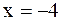 - не удовлетворяет условию
- не удовлетворяет условию 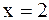 , то
, то 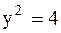 или
или 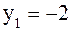 ,
, 
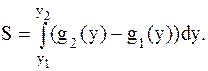
 ;
;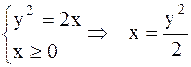 .
.
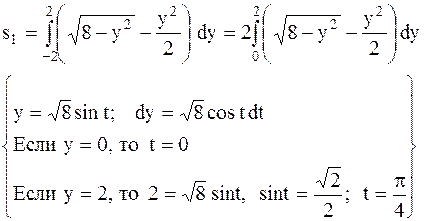

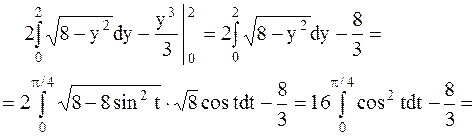
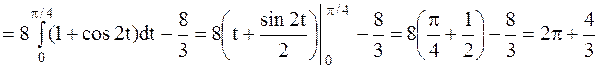 .
.