|
Сравнение полученных численных решений с точными значениями
Лабораторная работа № 5
Численное дифференцирование
Цель: освоить алгоритмы численного дифференцирования.
Задание:
1. Пусть сеточные представления функций заданы на отрезке [1,00; 1,20] для равномерного разбиения с шагом h=0,01. Найти значения:
1) первой производной с первым порядком точности в узлах сетки, используя направленные разности «вперед», «назад».
2) первой производной со вторым порядком точности в узлах сетки.
3) второй производной во внутренних узлах сетки.
2. Полученные значения сравнить с точными значениями и оценить погрешность в указанных точках. Вычислить
 , где , где 
 - точное значение производной в точке xi. - точное значение производной в точке xi.
Точное значение производной для указанных вариантов содержится в приложении 1.
3. Сопоставить  с теоретической оценкой погрешности. с теоретической оценкой погрешности.
| 1 вариант
| 
| | 2 вариант
| 
| | 3 вариант
| 
| | 4 вариант
| 
| | 5 вариант
| 
| | 6 вариант
| 
| | 7 вариант
| 
| | 8 вариант
| 
| | 9 вариант
| 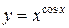
| | 10 вариант
| 
| | 11 вариант
| 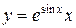
|
Ход работы
Пусть функция  задана таблично в узлах сетки: задана таблично в узлах сетки:
Таблица 10.1
| i
| xi
| yi
| |
|
| 0,841470985
| |
| 1,01
| 0,852160354
| |
| 1,02
| 0,862606646
| |
| 1,03
| 0,872795114
| |
| 1,04
| 0,882710803
| |
| 1,05
| 0,892338564
| |
| 1,06
| 0,901663063
| |
| 1,07
| 0,910668793
| |
| 1,08
| 0,919340088
| |
| 1,09
| 0,927661138
| |
| 1,1
| 0,935616002
| |
| 1,11
| 0,943188622
| |
| 1,12
| 0,950362847
| |
| 1,13
| 0,957122441
| |
| 1,14
| 0,963451109
| |
| 1,15
| 0,969332511
| |
| 1,16
| 0,974750287
| |
| 1,17
| 0,979688074
| |
| 1,18
| 0,984129532
| |
| 1,19
| 0,988058366
| |
| 1,2
| 0,991458348
|
Вычисление первой производной с первым порядком точности, используя направленные разности «вперед»
Найдем значения первой производной с первым порядком точности в узлах сетки, используя направленные разности «вперед». Вычисления будем производить по формуле
 (10.1) (10.1)
Вычислим значение первой производной по формуле (10.1) в узле х0:
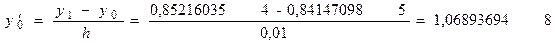
Результаты остальных вычислений поместим в таблицу 10.2
Таблица 10.2
| i
| xi
| yi
| y`i
| |
|
| 0,841470985
| 1,068936948
| |
| 1,01
| 0,852160354
| 1,044629206
| |
| 1,02
| 0,862606646
| 1,018846751
| |
| 1,03
| 0,872795114
| 0,991568918
| |
| 1,04
| 0,882710803
| 0,962776112
| |
| 1,05
| 0,892338564
| 0,932449879
| |
| 1,06
| 0,901663063
| 0,900572992
| |
| 1,07
| 0,910668793
| 0,867129538
| |
| 1,08
| 0,919340088
| 0,832104996
| |
| 1,09
| 0,927661138
| 0,795486334
| |
| 1,1
| 0,935616002
| 0,75726209
| |
| 1,11
| 0,943188622
| 0,717422466
| |
| 1,12
| 0,950362847
| 0,675959418
| |
| 1,13
| 0,957122441
| 0,63286675
| |
| 1,14
| 0,963451109
| 0,588140206
| |
| 1,15
| 0,969332511
| 0,541777566
| |
| 1,16
| 0,974750287
| 0,493778738
| |
| 1,17
| 0,979688074
| 0,444145858
| |
| 1,18
| 0,984129532
| 0,392883383
| |
| 1,19
| 0,988058366
| 0,339998187
| |
| 1,2
| 0,991458348
|
|
Вычисление первой производной с первым порядком точности, используя направленные разности «назад»
Найдем значения первой производной с первым порядком точности в узлах сетки, используя направленные разности «назад». Вычисления будем производить по формуле
 (10.2) (10.2)
Вычислим значение первой производной по формуле (10.2) в узле х1:

Результаты остальных вычислений поместим в таблицу 10.3
Таблица 10.3
| i
| xi
| yi
| y`i
| |
|
| 0,841470985
|
| |
| 1,01
| 0,852160354
| 1,068936948
| |
| 1,02
| 0,862606646
| 1,044629206
| |
| 1,03
| 0,872795114
| 1,018846751
| |
| 1,04
| 0,882710803
| 0,991568918
| |
| 1,05
| 0,892338564
| 0,962776112
| |
| 1,06
| 0,901663063
| 0,932449879
| |
| 1,07
| 0,910668793
| 0,900572992
| |
| 1,08
| 0,919340088
| 0,867129538
| |
| 1,09
| 0,927661138
| 0,832104996
| |
| 1,1
| 0,935616002
| 0,795486334
| |
| 1,11
| 0,943188622
| 0,75726209
| |
| 1,12
| 0,950362847
| 0,717422466
| |
| 1,13
| 0,957122441
| 0,675959418
| |
| 1,14
| 0,963451109
| 0,63286675
| |
| 1,15
| 0,969332511
| 0,588140206
| |
| 1,16
| 0,974750287
| 0,541777566
| |
| 1,17
| 0,979688074
| 0,493778738
| |
| 1,18
| 0,984129532
| 0,444145858
| |
| 1,19
| 0,988058366
| 0,392883383
| |
| 1,2
| 0,991458348
| 0,339998187
|
Вычисление первой производной со вторым порядком точности
Найдем значения первой производной со вторым порядком точности в узлах сетки. Вычисления будем производить по формулам:
 (10.3) (10.3)
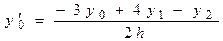 (10.4) (10.4)  (10.5) (10.5)
Вычислим значение первой производной по формуле (10.3) в узле х1:

Используя формулу (10.3.) вычислим значения первой производной со вторым порядком точности во внутренних узлах сетки, результаты вычислений поместим в таблицу 10.4. Значения в крайних узловых точках диапазона вычислим по формулам (10.4) – в точке х0, (10.5) - в точке х20.


Таблица 10.4
| i
| xi
| yi
| y`i
| |
|
| 0,841470985
| 1,081090818
| |
| 1,01
| 0,852160354
| 1,056783077
| |
| 1,02
| 0,862606646
| 1,031737979
| |
| 1,03
| 0,872795114
| 1,005207835
| |
| 1,04
| 0,882710803
| 0,977172515
| |
| 1,05
| 0,892338564
| 0,947612996
| |
| 1,06
| 0,901663063
| 0,916511436
| |
| 1,07
| 0,910668793
| 0,883851265
| |
| 1,08
| 0,919340088
| 0,849617267
| |
| 1,09
| 0,927661138
| 0,813795665
| |
| 1,1
| 0,935616002
| 0,776374212
| |
| 1,11
| 0,943188622
| 0,737342278
| |
| 1,12
| 0,950362847
| 0,696690942
| |
| 1,13
| 0,957122441
| 0,654413084
| |
| 1,14
| 0,963451109
| 0,610503478
| |
| 1,15
| 0,969332511
| 0,564958886
| |
| 1,16
| 0,974750287
| 0,517778152
| |
| 1,17
| 0,979688074
| 0,468962298
| |
| 1,18
| 0,984129532
| 0,418514621
| |
| 1,19
| 0,988058366
| 0,366440785
| |
| 1,2
| 0,991458348
| 0,31355559
|
Вычисление второй производной
Найдем значения второй производной со вторым порядком точности во внутренних узлах сетки. Вычисления будем производить по формуле:
 (10.6) (10.6)
Вычислим значение второй производной по формуле (10.6) в узле х1:

Результаты остальных вычислений поместим в таблицу 10.5
Таблица 10.5
| i
| xi
| yi
| y``i
| |
|
| 0,841470985
|
| |
| 1,01
| 0,852160354
| -2,43077411
| |
| 1,02
| 0,862606646
| -2,57824558
| |
| 1,03
| 0,872795114
| -2,72778322
| |
| 1,04
| 0,882710803
| -2,87928063
| |
| 1,05
| 0,892338564
| -3,03262334
| |
| 1,06
| 0,901663063
| -3,18768865
| |
| 1,07
| 0,910668793
| -3,34434548
| |
| 1,08
| 0,919340088
| -3,50245413
| |
| 1,09
| 0,927661138
| -3,6618662
| |
| 1,1
| 0,935616002
| -3,8224244
| |
| 1,11
| 0,943188622
| -3,98396241
| |
| 1,12
| 0,950362847
| -4,14630478
| |
| 1,13
| 0,957122441
| -4,3092668
| |
| 1,14
| 0,963451109
| -4,47265439
| |
| 1,15
| 0,969332511
| -4,63626406
| |
| 1,16
| 0,974750287
| -4,79988278
| |
| 1,17
| 0,979688074
| -4,96328799
| |
| 1,18
| 0,984129532
| -5,1262475
| |
| 1,19
| 0,988058366
| -5,28851956
| |
| 1,2
| 0,991458348
|
|
Сравнение полученных численных решений с точными значениями
Оценим погрешность полученных решений, сравнивая их с точными значениями первой и второй производной в узлах сетки. Результаты соответствующих вычислений поместим в таблицы 10.6, 10.7.
Таблица 10.6
| i
| xi
| точное 
|  Направленная разность
«вперед»
Направленная разность
«вперед»
|  Направленная разность
«назад»
Направленная разность
«назад»
|  Симметричная разность
Симметричная разность
| |
|
| 1,080604612
| 0,01166766
|
| 0,00048621
| |
| 1,01
| 1,05702709
| 0,01239788
| 0,01190986
| 0,00024401
| |
| 1,02
| 1,03198552
| 0,01313877
| 0,01264369
| 0,00024754
| |
| 1,03
| 1,005458734
| 0,01388982
| 0,01338802
| 0,0002509
| |
| 1,04
| 0,977426588
| 0,01465048
| 0,01414233
| 0,00025407
| |
| 1,05
| 0,947870045
| 0,01542017
| 0,01490607
| 0,00025705
| |
| 1,06
| 0,916771249
| 0,01619826
| 0,01567863
| 0,00025981
| |
| 1,07
| 0,884113617
| 0,01698408
| 0,01645937
| 0,00026235
| |
| 1,08
| 0,849881918
| 0,01777692
| 0,01724762
| 0,00026465
| |
| 1,09
| 0,814062361
| 0,01857603
| 0,01804264
| 0,0002667
| |
| 1,1
| 0,776642683
| 0,01938059
| 0,01884365
| 0,00026847
| |
| 1,11
| 0,737612239
| 0,02018977
| 0,01964985
| 0,00026996
| |
| 1,12
| 0,696962092
| 0,02100267
| 0,02046037
| 0,00027115
| |
| 1,13
| 0,654685109
| 0,02181836
| 0,02127431
| 0,00027202
| |
| 1,14
| 0,610776046
| 0,02263584
| 0,0220907
| 0,00027257
| |
| 1,15
| 0,565231649
| 0,02345408
| 0,02290856
| 0,00027276
| |
| 1,16
| 0,518050748
| 0,02427201
| 0,02372682
| 0,0002726
| |
| 1,17
| 0,469234348
| 0,02508849
| 0,02454439
| 0,00027205
| |
| 1,18
| 0,418785729
| 0,02590235
| 0,02536013
| 0,00027111
| |
| 1,19
| 0,366710542
| 0,02671235
| 0,02617284
| 0,00026976
| |
| 1,2
| 0,313016901
|
| 0,02698129
| 0,00053869
| 
| 0,02671235
| 0,02698129
| 0,00053869
|
Таблица 10.7
| i
| xi
| точное 
| 
| |
|
|
|
| |
| 1,01
| -2,43059363
| 0,000180479
| |
| 1,02
| -2,57807331
| 0,000172269
| |
| 1,03
| -2,72761982
| 0,000163403
| |
| 1,04
| -2,87912676
| 0,000153867
| |
| 1,05
| -3,03247969
| 0,000143644
| |
| 1,06
| -3,18755593
| 0,000132721
| |
| 1,07
| -3,34422439
| 0,000121083
| |
| 1,08
| -3,50234541
| 0,000108717
| |
| 1,09
| -3,66177059
| 9,56107E-05
| |
| 1,1
| -3,82234265
| 8,17529E-05
| |
| 1,11
| -3,98389528
| 6,71328E-05
| |
| 1,12
| -4,14625304
| 5,17412E-05
| |
| 1,13
| -4,30923123
| 3,55698E-05
| |
| 1,14
| -4,47263578
| 1,86116E-05
| |
| 1,15
| -4,6362632
| 8,60816E-07
| |
| 1,16
| -4,79990047
| 1,76867E-05
| |
| 1,17
| -4,96332502
| 3,70337E-05
| |
| 1,18
| -5,12630468
| 5,71814E-05
| |
| 1,19
| -5,28859769
| 7,81293E-05
| |
| 1,2
|
|
| 
| 0,000180479
|
3. Сопоставление  с теоретической оценкой погрешности с теоретической оценкой погрешности
Оценим теоретическую погрешность полученных решений.
3.1 Сопоставление  с теоретической оценкой погрешности для вычисления первой производной с первым порядком точности с теоретической оценкой погрешности для вычисления первой производной с первым порядком точности
Формулы(10.1), (10.2) имеют теоретическую погрешность
 (10.7), (10.7),
где 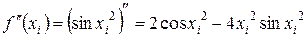 . .
 (10.8) (10.8)
Вычислим теоретическую погрешность для формулы (10.1) (направленная разность «вперед») результаты поместим в таблицу 10.8.
Таблица 10.8
| i
| xi
| Теоретическая погрешность 
| 
| |
|
| 0,011426397
| 0,01166766
| |
| 1,01
| 0,012152968
| 0,01239788
| |
| 1,02
| 0,012890367
| 0,01313877
| |
| 1,03
| 0,013638099
| 0,01388982
| |
| 1,04
| 0,014395634
| 0,01465048
| |
| 1,05
| 0,015162398
| 0,01542017
| |
| 1,06
| 0,01593778
| 0,01619826
| |
| 1,07
| 0,016721122
| 0,01698408
| |
| 1,08
| 0,017511727
| 0,01777692
| |
| 1,09
| 0,018308853
| 0,01857603
| |
| 1,1
| 0,019111713
| 0,01938059
| |
| 1,11
| 0,019919476
| 0,02018977
| |
| 1,12
| 0,020731265
| 0,02100267
| |
| 1,13
| 0,021546156
| 0,02181836
| |
| 1,14
| 0,022363179
| 0,02263584
| |
| 1,15
| 0,023181316
| 0,02345408
| |
| 1,16
| 0,023999502
| 0,02427201
| |
| 1,17
| 0,024816625
| 0,02508849
| |
| 1,18
| 0,025631523
| 0,02590235
| |
| 1,19
| 0,026442988
| 0,02671235
| |
| 1,2
|
|
| |
|
| 
| 
|
Из представленных в таблице (10.8) значений теоретической и практической погрешностей видно, что значения их имеют одинаковый порядок точности (≈ 2,6 · 10-2).
Формула (10.1) имеет первый порядок точности относительно шага h=0,01. Вычислим  и подставим полученное значение в формулу (10.8): и подставим полученное значение в формулу (10.8):
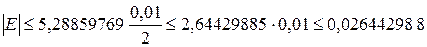 . .
Значение погрешности кроме шага сетки зависит от значения второй производной функции. В данном случае оно увеличило значение погрешности в 2,64429885 раза. Что подтверждено практической погрешностью.
Вычислим теоретическую погрешность для формулы (10.2) (направленная разность «назад») результаты поместим в таблицу 10.9.
Таблица 10.9
| i
| xi
| Теоретическая погрешность 
| 
| |
|
|
|
| |
| 1,01
| 0,012152968
| 0,01190986
| |
| 1,02
| 0,012890367
| 0,01264369
| |
| 1,03
| 0,013638099
| 0,01338802
| |
| 1,04
| 0,014395634
| 0,01414233
| |
| 1,05
| 0,015162398
| 0,01490607
| |
| 1,06
| 0,01593778
| 0,01567863
| |
| 1,07
| 0,016721122
| 0,01645937
| |
| 1,08
| 0,017511727
| 0,01724762
| |
| 1,09
| 0,018308853
| 0,01804264
| |
| 1,1
| 0,019111713
| 0,01884365
| |
| 1,11
| 0,019919476
| 0,01964985
| |
| 1,12
| 0,020731265
| 0,02046037
| |
| 1,13
| 0,021546156
| 0,02127431
| |
| 1,14
| 0,022363179
| 0,0220907
| |
| 1,15
| 0,023181316
| 0,02290856
| |
| 1,16
| 0,023999502
| 0,02372682
| |
| 1,17
| 0,024816625
| 0,02454439
| |
| 1,18
| 0,025631523
| 0,02536013
| |
| 1,19
| 0,026442988
| 0,02617284
| |
| 1,2
| 0,027249763
| 0,02698129
| |
|
| 
| 
|
Из представленных в таблице (10.9) значений теоретической и практической погрешностей видно, что значения их имеют одинаковый порядок точности (≈ 2,7 · 10-2).
Формула (10.2) имеет первый порядок точности относительно шага h=0,01. Вычислим 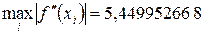 и подставим полученное значение в формулу (10.8): и подставим полученное значение в формулу (10.8):
 . .
Значение погрешности кроме шага сетки зависит от значения второй производной функции. В данном случае оно увеличило значение погрешности в 2,7249763 раза. Что подтверждено практической погрешностью.
3.2Сопоставление  с теоретической оценкой погрешности для вычисления первой производной со вторым порядком точности с теоретической оценкой погрешности для вычисления первой производной со вторым порядком точности
Формула (10.3) имеет второй порядок точности относительно шага h=0,01, ее теоретическая оценка погрешности равна:
 (10.9), (10.9),
где  . .
 , ,  (10.10) (10.10)
Формулы (10.4), (10.5) тоже имеют второй порядок точности относительно шага h=0,01, для них
 (10.11) (10.11)
и
 (10.12) (10.12)
соответственно.
Вычислим теоретическую погрешность по формулам (10.9), (10.11), (10.12) результаты поместим в таблицу 10.10.
Таблица 10.10
| i
| xi
| Теоретическая погрешность 
| 
| |
|
| 0,000480669
| 0,00048621
| |
| 1,01
| 0,000244021
| 0,00024401
| |
| 1,02
| 0,00024755
| 0,00024754
| |
| 1,03
| 0,000250909
| 0,0002509
| |
| 1,04
| 0,000254083
| 0,00025407
| |
| 1,05
| 0,00025706
| 0,00025705
| |
| 1,06
| 0,000259825
| 0,00025981
| |
| 1,07
| 0,000262365
| 0,00026235
| |
| 1,08
| 0,000264664
| 0,00026465
| |
| 1,09
| 0,000266709
| 0,0002667
| |
| 1,1
| 0,000268485
| 0,00026847
| |
| 1,11
| 0,000269975
| 0,00026996
| |
| 1,12
| 0,000271166
| 0,00027115
| |
| 1,13
| 0,000272041
| 0,00027202
| |
| 1,14
| 0,000272584
| 0,00027257
| |
| 1,15
| 0,000272781
| 0,00027276
| |
| 1,16
| 0,000272615
| 0,0002726
| |
| 1,17
| 0,000272069
| 0,00027205
| |
| 1,18
| 0,000271129
| 0,00027111
| |
| 1,19
| 0,000269778
| 0,00026976
| |
| 1,2
| 0,000535999
| 0,00053869
| i=0
 i=20
i=20
|
| 


| 


|
Формулы (10.3), (10.4), (10.5) имеют второй порядок точности относительно шага h=0,01.
Вычислим  . И подставим полученное решение в формулу (10.11) . И подставим полученное решение в формулу (10.11)

Значение погрешности кроме шага сетки зависит от значения третей производной функции. В данном случае оно увеличило значение погрешности в 4,80669009 раза. Что подтверждено практической погрешностью. Значения теоретической и практической погрешностей имеют одинаковый порядок точности (≈ 4,8 · 10-4).
Вычислим 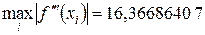 и подставим полученное значение в формулу (10.10): и подставим полученное значение в формулу (10.10):
 . .
Значение погрешности кроме шага сетки зависит от значения третей производной функции. В данном случае оно увеличило значение погрешности в 2,72781068 раза. Что подтверждено практической погрешностью. Значения теоретической и практической погрешностей имеют одинаковый порядок точности (≈ 2,7 · 10-4).
Вычислим  . И подставим полученное решение в формулу (10.12) . И подставим полученное решение в формулу (10.12)

Значение погрешности кроме шага сетки зависит от значения третей производной функции. В данном случае оно увеличило значение погрешности в 5,35999252 раза. Что подтверждено практической погрешностью. Значения теоретической и практической погрешностей имеют одинаковый порядок точности (≈ 5,4 · 10-4).
3.3Сопоставление  с теоретической оценкой погрешности для второй производной с теоретической оценкой погрешности для второй производной
Для формулы (10.6) теоретическая оценка погрешности производится по формуле
 (10.13), (10.13),
где 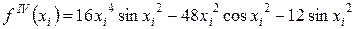 . .
 (10.14). (10.14).
Результаты вычислений по формуле (10.13) поместим в таблицу 10.11
Таблица 10.11
| i
| xi
| Теоретическая погрешность 
| 
| |
|
|
|
| |
| 1,01
| 0,000180501
| 0,000180479
| |
| 1,02
| 0,000172291
| 0,000172269
| |
| 1,03
| 0,000163426
| 0,000163403
| |
| 1,04
| 0,00015389
| 0,000153867
| |
| 1,05
| 0,000143667
| 0,000143644
| |
| 1,06
| 0,000132745
| 0,000132721
| |
| 1,07
| 0,000121107
| 0,000121083
| |
| 1,08
| 0,000108742
| 0,000108717
| |
| 1,09
| 9,56358E-05
| 9,56107E-05
| |
| 1,1
| 8,17783E-05
| 8,17529E-05
| |
| 1,11
| 6,71585E-05
| 6,71328E-05
| |
| 1,12
| 5,17672E-05
| 5,17412E-05
| |
| 1,13
| 3,5596E-05
| 3,55698E-05
| |
| 1,14
| 1,8638E-05
| 1,86116E-05
| |
| 1,15
| 8,87381E-07
| 8,60816E-07
| |
| 1,16
| 1,766E-05
| 1,76867E-05
| |
| 1,17
| 3,7007E-05
| 3,70337E-05
| |
| 1,18
| 5,71547E-05
| 5,71814E-05
| |
| 1,19
| 7,81027E-05
| 7,81293E-05
| |
| 1,2
|
|
| |
|
| 
| 
|
Из представленных в таблице (10.11) значений теоретической и практической погрешностей видно, что значения их имеют одинаковый порядок точности (≈ 1,8 · 10-4).
Формула (10.6) имеет второй порядок точности относительно шага h=0,01. Вычислим  и подставим полученное значение в формулу (10.14): и подставим полученное значение в формулу (10.14):
 . .
Значение погрешности кроме шага сетки зависит от значения четвертой производной функции. В данном случае оно увеличило значение погрешности в  раза. Что подтверждено практической погрешностью. раза. Что подтверждено практической погрешностью.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , где
, где 
 - точное значение производной в точке xi.
- точное значение производной в точке xi. с теоретической оценкой погрешности.
с теоретической оценкой погрешности.







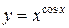

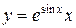
 задана таблично в узлах сетки:
задана таблично в узлах сетки: (10.1)
(10.1)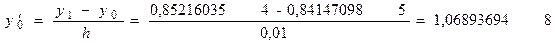
 (10.2)
(10.2)
 (10.3)
(10.3)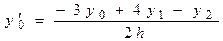 (10.4)
(10.4)  (10.5)
(10.5)


 (10.6)
(10.6)
 Симметричная разность
Симметричная разность



 (10.7),
(10.7),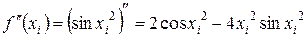 .
. (10.8)
(10.8)



 и подставим полученное значение в формулу (10.8):
и подставим полученное значение в формулу (10.8):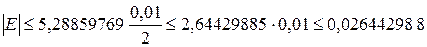 .
.

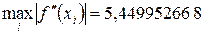 и подставим полученное значение в формулу (10.8):
и подставим полученное значение в формулу (10.8): .
. (10.9),
(10.9), .
. ,
,  (10.10)
(10.10) (10.11)
(10.11) (10.12)
(10.12) i=20
i=20






 . И подставим полученное решение в формулу (10.11)
. И подставим полученное решение в формулу (10.11)
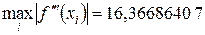 и подставим полученное значение в формулу (10.10):
и подставим полученное значение в формулу (10.10): .
. . И подставим полученное решение в формулу (10.12)
. И подставим полученное решение в формулу (10.12)
 (10.13),
(10.13),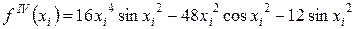 .
. (10.14).
(10.14).

 и подставим полученное значение в формулу (10.14):
и подставим полученное значение в формулу (10.14): .
. раза. Что подтверждено практической погрешностью.
раза. Что подтверждено практической погрешностью.