
|
|
Курсовой проект должен содержат следующие данные.УЧЕБНО – МЕТОДИЧЕСКОЕ ПОСОБИЕ к выполнению курсового проекта по курсу «Диагностика и надежность АС»
для студентов специализации «Автоматизация производственных процессов»
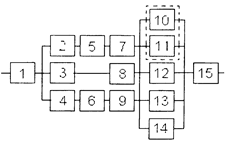
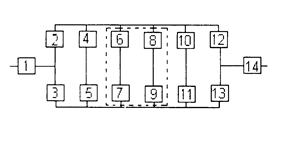
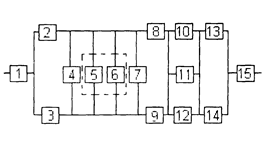
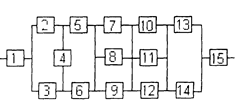
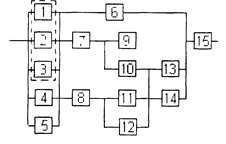
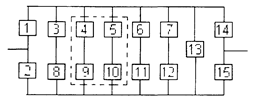
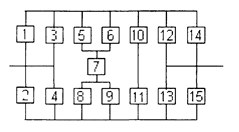
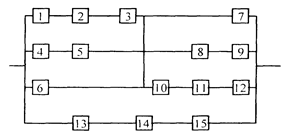
Уфа 2003 РАСЧЕТ НАДЕЖНОСТИ ИНФОРМАЦИОННОЙ СИСТЕМЫ Задание1/ По структурной схеме надежности информационной системы и заданным значениям интенсивности отказов ее элементов: 1) построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0,1 – 0,2; 2) определить время наработки системы соответствующее заданному γ (гамма-процентному ресурсу системы); 3) обеспечить при заданном γ (гамма-процентном ресурсе) увеличение времени наработки системы не менее чем в 1,5 раза за счет структурного резервирования элементов системы. Варианты структурных схем и значения интенсивностей отказов приведены на рис. 7 и в табл. 2, соответственно. Пример расчета Структурная схема надежности приведена на рис. 1.
Рис. 1.
Рис. 1
Значения интенсивности отказов элементов составляют:
где γ – (гамма-процентный ресурс системы) – вероятность безотказной работы системы, выраженный в процентах, по истечении определенного времени непрерывной работы (наработки) системы. Все элементы системы работают в режиме нормальной эксплуатации. Резервирование отдельных элементов или групп элементов должно осуществляться идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными. На схемах обведенные пунктиром m элементов являются функционально необходимыми. Расчет 1. В исходной схеме элементы 2 и 3 образуют параллельное соединение. Заменяем их квазиэлементом А. Учитывая, что p2 = p3, получим:
2. Элементы 4 и 5 также образуют параллельное соединение, заменив которое элементом В и учитывая, что p4 = p5, получим:
3. Элементы 6 и 7 в исходной схеме соединены последовательно. Заменяем их элементом С, для которого при p6 = p7: 4. Элементы 8 и 9 образуют параллельное соединение. Заменяем их элементом D, для которого при p8 = p9 , получим:
5. Элементы 10 и 11 образуют параллельное соединение. Заменяем их элементом Е, причем, так как p10 = p11 = p8, то
6. Элементы 12, 13, 14 и 15 образуют соединение «2 из 4», которое заменяем элементом F. Так как p12 = p13 = p14 = p15, то для определения вероятности безотказной работы элемента F можно воспользоваться выражением, в основе которого лежит формула биноминального распределения (биноминальному распределению подчиняется дискретная случайная величина k – число появлений некоторого события в серии из n опытов, если в отдельном опыте вероятность появления события составляет p).
где
Поскольку для отказа системы «m из n» достаточно, чтобы количество исправных элементов было меньше m, вероятность отказа может быть найдена по теореме сложения вероятностей для k = 0, 1, …, (m – 1):
Аналогичным образом можно найти вероятность безотказной работы как сумму для k = m, m + 1, …, n:
В данном конкретном случае, при n = 4 и m = 2, вероятность безотказной работы элемента F определится выражением:

7. Преобразованная схема изображена на рис. 2.
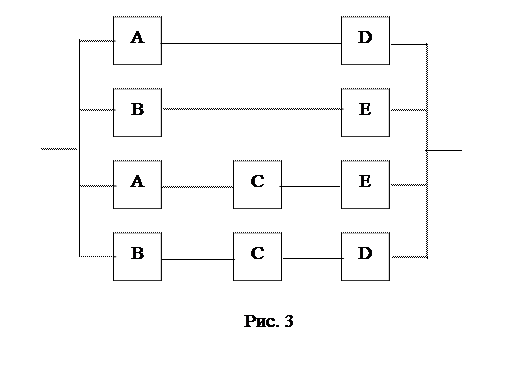
Рис. 2 8. Элементы А, В, С, D и Е (рис. 2) образуют мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом минимальных путей. Логическая схема мостиковой системы по методу минимальных путей приведена на рис. 3
Система, изображенная на рис. 3 работоспособна до тех пор, пока работоспособны элементы А и D или – B и E, или – A, C и E, или – B, C и D. Таким образом, вероятность работы квазиэлемента G можно определить по формуле:
9. После преобразования схема примет вид, изображенный на рис. 4.
Рис. 4
10. В преобразованной схеме (рис. 4) элементы 1, G, и F образуют последовательное соединение. Тогда вероятность безотказной работы всей системы определяется выражением:
11. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 1) подчиняются экспоненциальному закону:
12. Результаты расчетов вероятностей безотказной работы элементов 1 – 15 исходной схемы по формуле (9) для наработки до 3·106 часов представлены в табл. 1. Таблица 1
13. Результаты расчетов вероятностей безотказной работы квазиэлементов А, В, С, D, Е, F и G по формулам (1) – (7) и также представлены в табл. 1. 14. На рис. 5 представлен график зависимости вероятности безотказной работы системы Р от времени (наработки) t.
 
Рис. 5
15. По графику (рис. 5, кривая Р) находим для γ = 50% (Р = 0.5) γ-процентную наработку системы t = 1,9·106 ч. 16. Проверочный расчет при t = 1,9·106 ч показывает (табл. 1), что 17. По условиям задания находим время, превышающее в 1,5 раза время, соответствующее вероятности безотказной работы, равное 0,5 (Pγ = 0,5):
18. Расчет показывает (табл. 1), что при 19. Для того чтобы при
где
20. Для элемента F системы «2 из 4» резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов достаточно сложно, так как число элементов должно быть целым и функция 21. Для повышения надежности системы «2 из 4» добавляем к ней элементы, идентичные по надежности исходным элементам 12 – 15, до тех пор, пока вероятность безотказной работы квазиэлемента F не достигнет заданного значения: - добавляем элемент 16, получаем систему «2 из 5»:

- добавляем элемент 17, получаем систему «2 из 6»:
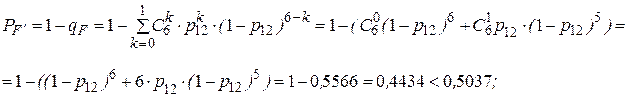
- добавляем элемент 18, получаем систему «2 из 7»:

23. Результаты расчетов вероятностей безотказной работы квазиэлемента «F» («2 из 7») и системы в целом Р’ представлены в табл. 1. 24. Расчеты показывают, что при t’ = 2,85×106 ч, Р’ = 0,5272 > 0,5, что соответствует условию задания.
ВЫВОД
1. По данным расчета вероятности безотказной работы системы от времени построен график P(t). 2. По графику найдено время, соответствующее 50% g-процентному ресурсу системы (t = 1,9 × 106 ч). 3. Для увеличения наработки системы в 1,5 раза при 50% g -процентном ресурсе системы предложено нагруженное резервирование основных элементов 12, 13, 14 и 15 идентичными по надежности резервными элементами 16, 17 и 18. 4. Рассчитана вероятность безотказной работы системы с повышенной надежностью от времени, построен график P’(t) системы с повышенной надежностью, на графике (рис. 7) показано время (t’ = 2,85 × 106 ч) соответствующее 50% g -процентному ресурсу.
 
 
 
 
Таблица 2 Численные значения параметров к заданию
Продолжение табл. 2
Задание 2 Расчет показателей надежности систем автоматизации (СА) с восстановлением(метод Колмогорова).
2.1. Исходные данные выбираются из таблицы 3. 2.2. Структурная схема состояний системы. 2.3.Система уравнений Колмогорова и ее решение для установившегося режима. 2.4. Определение коэффициентов готовности и простоя системы. Интенсивность отказа основного и резервных элементов принят равным 0,1, а интенсивность восстановления 0,5
Курсовой проект должен содержат следующие данные.
3.1. Титульный лист. 3.2. Содержание. 3.3 Изложение всех пунктов задания. 3.4. Выводы в конце каждого раздела. 3.5. Список использованных источников.
Полезные рекомендации
При выполнении задания 2 можно воспользоваться книгой под редакцией Дружинина Г.В. Теория надежности радиоэлектронных систем. – М.: Энергия, 1976., где приведено множество примеров.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

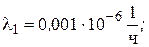
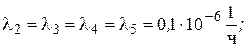
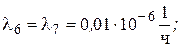
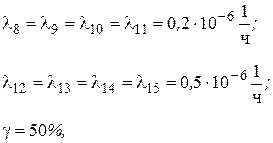
 (1)
(1) (2)
(2)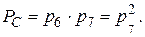 (3)
(3)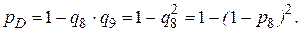 (4)
(4) (5)
(5)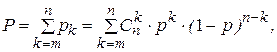
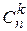 – биноминальный коэффициент, называемый «числом сочетаний по k из n» (т. е. сколькими разными способами можно реализовать ситуацию k из n).
– биноминальный коэффициент, называемый «числом сочетаний по k из n» (т. е. сколькими разными способами можно реализовать ситуацию k из n). .
.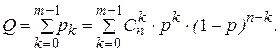
 .
.

 (7)
(7)
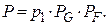 (8)
(8) (9)
(9)
 . (10)
. (10) = 1,5·1,9·106 = 2,85·106 ч.
= 1,5·1,9·106 = 2,85·106 ч.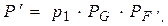
 – необходимая вероятность безотказной работы элемента F, то
– необходимая вероятность безотказной работы элемента F, то (11)
(11)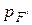 = f(n) дискретна.
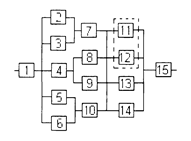
= f(n) дискретна. 22. Таким образом, для повышения надежности до требуемого уровня, необходимо в исходной схеме (рис. 1) систему «2 из 4» достроить элементами 16, 17 и 18 до системы «2 из 7» (рис. 6).
22. Таким образом, для повышения надежности до требуемого уровня, необходимо в исходной схеме (рис. 1) систему «2 из 4» достроить элементами 16, 17 и 18 до системы «2 из 7» (рис. 6).



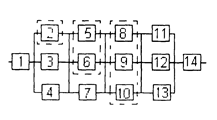

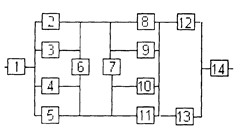

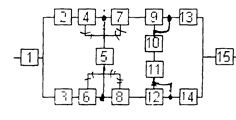






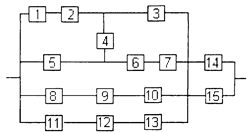

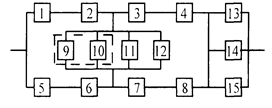

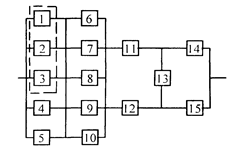


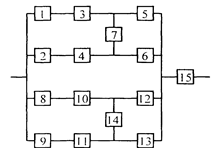
 Интенсивности отказов элементов, х10-6 1/ч
Интенсивности отказов элементов, х10-6 1/ч