Интеграл с переменным верхним пределом.
Пусть f(x) непрерывна на [a;b] и потому интегрируема на [a;x] , где х  b. В этом случае b. В этом случае  f(t)dt зависит от х. Т.е. f(t)dt зависит от х. Т.е.  f(t)dt=Ф(х). f(t)dt=Ф(х).
Теорема. Ф(х) – непрерывна на [a;b]. Док. Вычислим  Ф(х)= Ф(х+ Ф(х)= Ф(х+  х)- Ф(х)= х)- Ф(х)=  f(t)dt, который по теореме о среднем равен f(C) f(t)dt, который по теореме о среднем равен f(C)  х. Где С между х и х+ х. Где С между х и х+  х. Т.е. х. Т.е.  Ф(х)= f(C) Ф(х)= f(C)  х. Если х. Если  хà0, то хà0, то  Ф(х) à0, а значит Ф(х) – непрерывна. Ф(х) à0, а значит Ф(х) – непрерывна.
Теорема. Ф(х) – дифференцируема на [a;b]. Док. По найденному приращению  Ф(х) найдем Ф(х) найдем  =f(x) – cм.выше. =f(x) – cм.выше.
Т.е. Ф’(х)=(  f(t)dt)’x =f(x). Аналогично ( f(t)dt)’x =f(x). Аналогично (  f(t)dt)’x =-f(x). f(t)dt)’x =-f(x).
Следствие. Производная по верхнему пределу от интеграла с переменным верхним пределом равна значению подынтегральной функции в верхнем пределе.
Комментарий. Фактически доказана теорема существования неопределенного интеграла. Именно  f(x)dx= f(x)dx=  f(t)dt+C. f(t)dt+C.
Из этих рассуждений следует формула Ньютона-Лейбница  f(x)dx =F(b)-F(a). Док. Имеем Ф(х) = f(x)dx =F(b)-F(a). Док. Имеем Ф(х) =  f(t)dt. Пусть F(x) – любая из этих первообразных. Т.е. f(t)dt. Пусть F(x) – любая из этих первообразных. Т.е.
 f(t)dt= F(x)+C. Из этого равенства при х=а получаем F(a)=-C. Или f(t)dt= F(x)+C. Из этого равенства при х=а получаем F(a)=-C. Или  f(t)dt= F(x)-F(a). С другой стороны при х=b из того же равенства получаем f(t)dt= F(x)-F(a). С другой стороны при х=b из того же равенства получаем
 f(x)dx= F(b)-F(a). (7.2) f(x)dx= F(b)-F(a). (7.2)
2.3.Замена переменной в определенном интеграле и интегрирование по частям.
Теорема. Если х=ф(t) непрерывна на [  ; ;  ] оси t вместе со своей производной x’=ф’(t); при изменении t от ] оси t вместе со своей производной x’=ф’(t); при изменении t от  до до  значение ф(t) не выходит за пределы [a;b]; ф( значение ф(t) не выходит за пределы [a;b]; ф(  )=а , ф( )=а , ф(  ) = b, то для непрерывной на [a;b] функции f(x) справедливо равенство ) = b, то для непрерывной на [a;b] функции f(x) справедливо равенство  f(x)dx= f(x)dx=  f(ф(t))ф’(t)dt (7.3) f(ф(t))ф’(t)dt (7.3)
называемое формулой замены переменной в определенном интеграле.
Док. В самом деле  f(t)dt= F(b)-F(a) , где F(x) первообразная для f(x). Т.к. при этом F(ф(t)) – есть первообразная для f(ф(t))ф’(t), непрерывной на f(t)dt= F(b)-F(a) , где F(x) первообразная для f(x). Т.к. при этом F(ф(t)) – есть первообразная для f(ф(t))ф’(t), непрерывной на
[  ; ;  ], то По Ньютону-Лейбницу имеем ], то По Ньютону-Лейбницу имеем  f(ф(t))ф’(t)dt =F(ф( f(ф(t))ф’(t)dt =F(ф(  )) - F(ф( )) - F(ф(  ))= F(b)-F(a) = ))= F(b)-F(a) =  f(t)dt. f(t)dt.
Комментарий. Имеются два подхода использования формулы замены. Один из них изложен выше. В другом (более употребимом) случае заменяют не переменную х, на некоторое выражение, а выражение, связывающее х заменяют одной переменной. А далее – как обычно. Не следует забывать также о смене пределов интегрирования в момент замены, чтобы не возвращаться к исходной переменной.
Интегрирование по частям. Пусть u=ф(х) и v=f(x) непрерывны и дифференцируемы на [a;b]. Проинтегрируем равенство (uv)’=u’v+v’u на этом отрезке и получим  (uv)’dx= (uv)’dx=  u’vdx + u’vdx +  v’udx. Но т.к. uv есть первообразная для (uv)’, то получаем v’udx. Но т.к. uv есть первообразная для (uv)’, то получаем  v’udx = uv v’udx = uv  - -  u’vdx (7.3) u’vdx (7.3)
Формулу (7.3) называют формулой интегрирования по частям в ОИ.
Несобственные интегралы.
Пусть f(x) непрерывна на [a; +  ). Тогда она непрерывна и на [a;b] и потому ). Тогда она непрерывна и на [a;b] и потому  f(х)dх= F(b) – некоторая функция от предела b. f(х)dх= F(b) – некоторая функция от предела b.
Опред. Если при bà+  существует существует  и равен конечному числу, то этот предел обозначают символом и равен конечному числу, то этот предел обозначают символом  f(х)dх, называют несобственным интегралом с бесконечным верхним пределом и считают сходящимся. В противном случае символу f(х)dх, называют несобственным интегралом с бесконечным верхним пределом и считают сходящимся. В противном случае символу  f(х)dх ничего не приписывают, называют так же и считают расходящимся. f(х)dх ничего не приписывают, называют так же и считают расходящимся.
Аналогично дают определение символу  f(х)dх . Если же имеется символ f(х)dх . Если же имеется символ  f(х)dх, то в нем сначала заменяют бесконечные пределы конечными параметрами, затем на отрезке между параметрами берут произвольную точку и вычисляют два предела : f(х)dх, то в нем сначала заменяют бесконечные пределы конечными параметрами, затем на отрезке между параметрами берут произвольную точку и вычисляют два предела :  и и  . Если хотя бы один из этих пределов не существует или равен бесконечности, то исходный символ называют несобственным с бесконечными пределами и расходящимся. Сходящимся он будет только, если оба слагаемые сходятся. . Если хотя бы один из этих пределов не существует или равен бесконечности, то исходный символ называют несобственным с бесконечными пределами и расходящимся. Сходящимся он будет только, если оба слагаемые сходятся.
Зачастую работать с определением затруднительно. Тогда используют признаки сходимости.
Теорема. (признак сравнения) Если 0  g(x) g(x)  f(x) и для любого х из f(x) и для любого х из
[a; +  ) интеграл ) интеграл  f(х)dх сходится, то сходится и интеграл f(х)dх сходится, то сходится и интеграл  g(х)dх. Если же при указанных условиях интеграл g(х)dх. Если же при указанных условиях интеграл  g(х)dх расходится, то расходится и интеграл g(х)dх расходится, то расходится и интеграл  f(х)dх. f(х)dх.
Док. Вытекает из интегрирования неравенства.
Теорема. (предельный признак сравнения) Если  =k не равному нулю и не равному =k не равному нулю и не равному  , то интегралы , то интегралы  g(х)dх и g(х)dх и  f(х)dх ведут себя одинаково в смысле сходимости. (без док.) f(х)dх ведут себя одинаково в смысле сходимости. (без док.)
Комментарий.
В качестве ‘лакмусовой’ бумажки (мерительного инструмента) используют интеграл от степенной функции J=   = =  . Иначе говоря при р больших 1 интеграл сходится, а в других случаях – расходится. . Иначе говоря при р больших 1 интеграл сходится, а в других случаях – расходится.
Опр. Если интеграл   f(х) f(х)  dх сходится, то сходится и интеграл dх сходится, то сходится и интеграл  f(х)dх и тогда последний называют абсолютно сходящимся. f(х)dх и тогда последний называют абсолютно сходящимся.
Опр. Если интеграл   f(х) f(х)  dх расходится, а интеграл dх расходится, а интеграл  f(х)dх сходится, тогда последний называют условно сходящимся. f(х)dх сходится, тогда последний называют условно сходящимся.
Пример. 7.7.  . Выясним его характер. Для чего сравним подынтегральную функцию по модулю с функцией . Выясним его характер. Для чего сравним подынтегральную функцию по модулю с функцией  . Имеем . Имеем    < <  . А потому исходный интеграл сходится абсолютно. . А потому исходный интеграл сходится абсолютно.
Пусть f(x) непрерывна на [a;b] и имеет разрыв 2-го рода (неограниченна) в точке b. Тогда f(x) интегрируема на [a;b1] для b1<b. В этом случае  f(х)dх=Ф(b1) – функция от b1. f(х)dх=Ф(b1) – функция от b1.
Опр. Если существует конечный  , то его обозначают символом , то его обозначают символом  f(х)dх, называют несобственным интегралом от разрывной функции и считают сходящимся. f(х)dх, называют несобственным интегралом от разрывной функции и считают сходящимся.
В противном случае указанному символу ничего не приписывают и называют расходящимся несобственным интегралом от разрывной функции.
Аналогичная ситуация для непрерывной f(x) на [a;b] за исключением некоторой С  [a;b]. В этом случае рассматривают два несобственных интеграла от разрывной функции на двух интервалах [a;С] и [С;b]. Если хотя бы одно слагаемое – интеграл расходящийся, то исходный интеграл считают расходящимся. В противном случае интеграл считают сходящимся. [a;b]. В этом случае рассматривают два несобственных интеграла от разрывной функции на двух интервалах [a;С] и [С;b]. Если хотя бы одно слагаемое – интеграл расходящийся, то исходный интеграл считают расходящимся. В противном случае интеграл считают сходящимся.
Из последних определений следует, что до вычисления  f(х)dх следует проверить, будет ли символ несобственного интеграла или это определенный интеграл. И только после этого приниматься за вычисления(работу). f(х)dх следует проверить, будет ли символ несобственного интеграла или это определенный интеграл. И только после этого приниматься за вычисления(работу).
Если же установить характер сходимости по определению затруднительно используют признаки сравнения с интегралом J=   = = 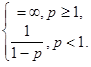 . Иначе говоря, при p<1 интеграл сходится, в противном случае – расходится. . Иначе говоря, при p<1 интеграл сходится, в противном случае – расходится.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 b. В этом случае
b. В этом случае  f(t)dt зависит от х. Т.е.
f(t)dt зависит от х. Т.е.  Ф(х)= Ф(х+
Ф(х)= Ф(х+  f(t)dt, который по теореме о среднем равен f(C)
f(t)dt, который по теореме о среднем равен f(C)  =f(x) – cм.выше.
=f(x) – cм.выше. f(t)dt)’x =-f(x).
f(t)dt)’x =-f(x). f(x)dx=
f(x)dx=  f(x)dx =F(b)-F(a). Док. Имеем Ф(х) =
f(x)dx =F(b)-F(a). Док. Имеем Ф(х) =  ;
;  ] оси t вместе со своей производной x’=ф’(t); при изменении t от
] оси t вместе со своей производной x’=ф’(t); при изменении t от  f(ф(t))ф’(t)dt (7.3)
f(ф(t))ф’(t)dt (7.3) -
-  ). Тогда она непрерывна и на [a;b] и потому
). Тогда она непрерывна и на [a;b] и потому  и равен конечному числу, то этот предел обозначают символом
и равен конечному числу, то этот предел обозначают символом  f(х)dх, называют несобственным интегралом с бесконечным верхним пределом и считают сходящимся. В противном случае символу
f(х)dх, называют несобственным интегралом с бесконечным верхним пределом и считают сходящимся. В противном случае символу  f(х)dх . Если же имеется символ
f(х)dх . Если же имеется символ  f(х)dх, то в нем сначала заменяют бесконечные пределы конечными параметрами, затем на отрезке между параметрами берут произвольную точку и вычисляют два предела :
f(х)dх, то в нем сначала заменяют бесконечные пределы конечными параметрами, затем на отрезке между параметрами берут произвольную точку и вычисляют два предела :  и
и  . Если хотя бы один из этих пределов не существует или равен бесконечности, то исходный символ называют несобственным с бесконечными пределами и расходящимся. Сходящимся он будет только, если оба слагаемые сходятся.
. Если хотя бы один из этих пределов не существует или равен бесконечности, то исходный символ называют несобственным с бесконечными пределами и расходящимся. Сходящимся он будет только, если оба слагаемые сходятся. =k не равному нулю и не равному
=k не равному нулю и не равному 
 =
=  . Иначе говоря при р больших 1 интеграл сходится, а в других случаях – расходится.
. Иначе говоря при р больших 1 интеграл сходится, а в других случаях – расходится. f(х)
f(х)  dх сходится, то сходится и интеграл
dх сходится, то сходится и интеграл  . Выясним его характер. Для чего сравним подынтегральную функцию по модулю с функцией
. Выясним его характер. Для чего сравним подынтегральную функцию по модулю с функцией  . Имеем
. Имеем 
 f(х)dх=Ф(b1) – функция от b1.
f(х)dх=Ф(b1) – функция от b1. , то его обозначают символом
, то его обозначают символом  [a;b]. В этом случае рассматривают два несобственных интеграла от разрывной функции на двух интервалах [a;С] и [С;b]. Если хотя бы одно слагаемое – интеграл расходящийся, то исходный интеграл считают расходящимся. В противном случае интеграл считают сходящимся.
[a;b]. В этом случае рассматривают два несобственных интеграла от разрывной функции на двух интервалах [a;С] и [С;b]. Если хотя бы одно слагаемое – интеграл расходящийся, то исходный интеграл считают расходящимся. В противном случае интеграл считают сходящимся.
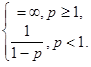 . Иначе говоря, при p<1 интеграл сходится, в противном случае – расходится.
. Иначе говоря, при p<1 интеграл сходится, в противном случае – расходится.