
|
|
Вычисление площадей плоских фигур.12 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Методические указания по дисциплине «Математический анализ» для студентов дневной формы обучения
Хабаровск Издательство ТОГУ 2007 УДК 22.17
Интегральное исчисление: методические указания по дисциплине «Математический анализ» для студентов дневной формы обучения / сост. Н.Б Лазарева, Н.Н.Ловцова – Хабаровск : Изд-во Тихоокеан. гос. ун-та, 2007. – 31с.
Методические указания составлены на кафедре прикладной математики информатики. В них изложены основные методы вычисления неопределённого интеграла, приложения определенного интеграла, рассмотрены примеры решения задач.
Печатается в соответствии с решениями кафедры «Прикладная математика и информатика» и методического совета факультета математического моделирования и процессов управления.
Ó Тихоокеанский государственный университет,2007 § 1. Неопределённый интеграл
Функция F(x) называется первообразной для функции f(x), если
Всякая непрерывная функция f(x) имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым.
Неопределённым интегралом от функции f(x) называется совокупность всех её первообразных: Здесь
Свойства неопределённого интеграла: 1. 2. 3. 4. Если 5. Если
Правильность результата интегрирования проверяется дифференцированием найденной первообразной, т.е.
Таблица основных интегралов представлена в приложении 1.
Задача нахождения неопределённых интегралов от многих функций решается методом сведения их к одному из табличных интегралов. Этого можно достичь путём алгебраических тождественных преобразований подынтегральной функции f(x) или подведения части её множителей под знак дифференциала.
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Если функция неопределённом интеграле
затем найти интеграл и вернуться к исходной переменной х. Такой способ нахождения интеграла называется методом замены переменной или методом подстановки.
Пример 5.
Пример 6.
Пример 7.
Пример 8.
§ 4. Интегрирование по частям.
Интегрированием по частям называется нахождение интеграла по формуле
где u(x) и v(x) - дифференцируемые функции.
Применение её целесообразно, когда интеграл в правой части формулы более прост для нахождения, нежели исходный. В некоторых случаях формулу необходимо применять несколько раз. При этом за u(x) берётся такая функция, которая при дифференцировании упрощается, а за dv -та часть подынтегрального выражения, интеграл от которой известен или может быть найден. Так, например, для интегралов вида за u(x) следует принять многочлен P(x) . Для интегралов вида за u(x) принимаются функции lnx, arcsinx, arctgx, а за dv - выражение P(x)dx .
Пример 9.
Пример 10.
Пример 11.
Циклические интегралы
Пример12.
Отсюда получаем
§ 5. Интегрирование рациональных функций.
Рациональной называется функция вида
где m,n-целые, положительные числа. Если m<n,то R(x) называется правильной дробью, если m Так как всякий многочлен легко интегрируется, то интегрирование рациональных функций сводится к интегрированию правильных дробей. Всякую правильную рациональную дробь можно разложить в сумму простейших рациональных дробей типа:
1.
2.
3. не имеет действительных корней
4.
Вычисление интеграла
Пример 13.
Пример 14.
Пример 15.
Пример 16.
Вычислим первый интеграл:
Вычислим второй интеграл, используя рекуррентную формулу, где к = 2:
Итоговый результат:
Метод интегрирования рациональных дробей в целом рассмотрим на следующем примере:
Пример 17.
Разложим подынтегральную дробь на простейшие дроби :
Освободимся от знаменателей, умножая обе части равенства на
Приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, получаем систему уравнений:
решение которой Подставляя под знак интеграла полученную сумму элементарных дробей, имеем:
1. Интегралы вида знаменатель дробей
Пример18.
2. Интегралы вида числа подстановки
Пример 19.
3. Интегралы вида числа 1) если трёхчлен
случай. 2) если трёхчлен интеграл преобразуется подстановкой Эйлера
3) если трёхчлен то применяют другую подстановку Эйлера
4) выделим полный квадрат: С помощью подстановки от коэффициентов
Пример 20.
функций.
1. Интегралы вида Пример 21.
2. Интегралы вида чётные числа, вычисляются с помощью формул:
Пример 22.
Если n-нечётное положительное число, то применяется подстановка sinx = t, если m-нечётное положительное число, то применяется подстановка cosx = t.
Пример 23.
В общем случае интегралы этого вида вычисляются с помощью рекуррентных формул, которые выводятся путём интегрирования по частям.
Пример 24.
Второй интеграл – табличный, первый вычислим интегрированием по частям:
Итоговый результат:
3. Интегралы вида где
Пример 25.
4. Интегралы вида с помощью формул
Пример 26.
5.Интегрирование гиперболических функций производится аналогично интегрированию тригонометрических функций, причём используются следующие формулы:
Пример 27.
Пусть функция x0=a, x1, x2, …, xn=b разобьем отрезок [a, b] на n частичных отрезков [x0, x1], [x1, x2], … ,[xn-1, xn]
с1 с2 сi cn
a=x0 x1 x2 xi-1 xi xn-1 b=xn
В каждом частичном отрезке [xi-1, xi] выберем произвольную точку сi и вычислим f(ci). Составим сумму
где
Обозначим через
Свойства определенного интеграла : 1. 2.
3. 4.
5.
6. 7. 8. 9.
10. Если такая точка
(Обобщённая теорема о среднем) Число
1. Если функция первообразная формула Ньютона-Лейбница
Пример 28. 2.Интегрирование заменой переменной: Если функция
Пример 29.
3. Интегрирование по частям:Если функции непрерывные производные на отрезке
Пример 30.
Замечание: в Приложении 2 предлагаются задания для закрепления навыков вычисления неопределённого и определённого интегралов.
Вычисление площадей плоских фигур. a) Площадь криволинейной трапеции, ограниченной графиком непрерывной функции и осью ОХ вычисляется по формуле:
(если х есть функция переменной у)
 

Площадь фигуры, ограниченной графиками непрерывных функций вычисляется по формуле:
b) Площадь фигуры, ограниченной кривой, заданной параметрическими уравнениями
c) Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением
Пример 31. Найти площадь фигуры, ограниченной кривой
Решение:
 
Пример 32. Найти площадь фигуры, ограниченной эллипсом Решение:
 

Пример 33. Найти площадь фигуры, ограниченной параболой
Решение:




12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 или
или  .
. .
.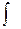 -знак интеграла, f(x) –подынтегральная функция, х –переменная интегрирования.
-знак интеграла, f(x) –подынтегральная функция, х –переменная интегрирования.
 , где
, где 


 -любая дифференцируемая функция, то
-любая дифференцируемая функция, то  .
. ,
, и
и 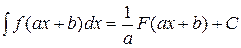 .
.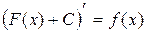 .
.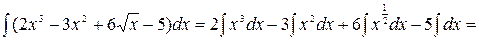
 .
.



 =
= 
 имеет непрерывную производную, то в
имеет непрерывную производную, то в можно перейти к новой переменной t по формуле
можно перейти к новой переменной t по формуле ,
,


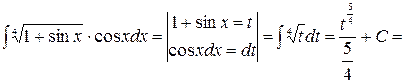



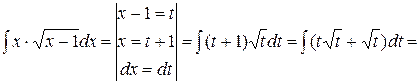

 ,
, ,
,  ,
, 
 ,
,  ,
, 








 ,
,  находятся двукратным интегрированием по частям.
находятся двукратным интегрированием по частям.




 n ,то неправильной. Всякую неправильную дробь путём деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби:
n ,то неправильной. Всякую неправильную дробь путём деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби:  , l<n.
, l<n.

 , где к -целое число, больше единицы
, где к -целое число, больше единицы
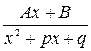 , где
, где 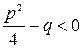 , т.е. квадратный трёхчлен
, т.е. квадратный трёхчлен 


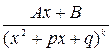

 производится по рекуррентной формуле :
производится по рекуррентной формуле :

















 :
:



 .
.

 , где R-рациональная функция,
, где R-рациональная функция,  -целые числа преобразуются в интегралы от рациональных функций с помощью подстановки
-целые числа преобразуются в интегралы от рациональных функций с помощью подстановки  ,где к-общий
,где к-общий

 .
.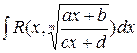 , где
, где  -некоторые
-некоторые m-натуральное число, преобразуются с помощью
m-натуральное число, преобразуются с помощью .
. .
.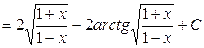
 , где
, где  -некоторые
-некоторые :
: имеет вещественные корни
имеет вещественные корни  и
и  >0, то
>0, то и
и . Имеем предыдущий
. Имеем предыдущий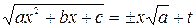 .
. .
. .
. интеграл сводится в зависимости
интеграл сводится в зависимости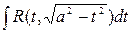 замена
замена 
 замена
замена 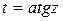 или
или 
 замена
замена  или
или 



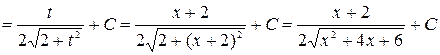
 , где R-рациональная функция, приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки
, где R-рациональная функция, приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки  .
.

 .
. , где m и n-положительные целые
, где m и n-положительные целые


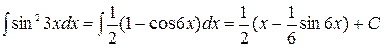 .
.


 .
.




 ,
, 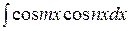 ,
,  ,
, , вычисляются с помощью формул:
, вычисляются с помощью формул:




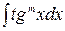 ,
,  , где m = 2,3,… вычисляются
, где m = 2,3,… вычисляются ,
, 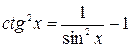 .
.

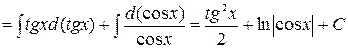







 определена на отрезке [a, b]. С помощью точек
определена на отрезке [a, b]. С помощью точек

 , которая называется интегральной суммой функции
, которая называется интегральной суммой функции . Найдем предел
. Найдем предел  , когда
, когда  , так что
, так что . Если интегральная сумма Sn имеет предел
. Если интегральная сумма Sn имеет предел  , который не зависит ни от способа разбиения отрезка [a, b] на частичные отрезки, ни от выбора точек в них, то число
, который не зависит ни от способа разбиения отрезка [a, b] на частичные отрезки, ни от выбора точек в них, то число  .
.



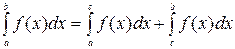 ,
, 


 , если
, если  <
< 


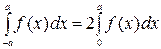 , если функция
, если функция  - чётная.
- чётная. , если функция
, если функция  интегрируема на
интегрируема на  , то существует
, то существует , что справедливо равенство
, что справедливо равенство .
. называется средним значением функции
называется средним значением функции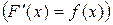 , то справедлива
, то справедлива .
.
 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 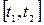 , причём
, причём  ,
,  , то
, то  .
.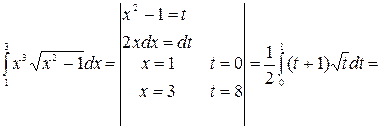

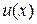 и
и  имеют
имеют



 , прямыми
, прямыми  и
и 
 или
или 


 и
и 
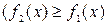 , прямыми
, прямыми  .
. , прямыми
, прямыми  и осью ОХ вычисляется по формуле:
и осью ОХ вычисляется по формуле:  , где пределы интегрирования находятся из уравнений
, где пределы интегрирования находятся из уравнений
 на
на  и лучами
и лучами  и
и  вычисляется по формуле:
вычисляется по формуле: .
. .
.



 ,
,  .
.

 и осью ОХ.
и осью ОХ.
