
|
|
Вычисление площади в полярной системе координат и кривой заданной параметрически.12 Если в декартовой системе координат вычисляется площадь криволинейной трапеции, то в полярной системе вычисляется площадь криволинейного сектора. Определение: Криволинейным сектором называется фигура, заключенная между двумя лучами, выходящими из полюса под углами j=a и j=b и кривой, заданной в полярной системе координат r=r(j). Разобьем криволинейный сектор лучами j=j i, i = 0…n на части a=j0 <j1<j2<…<jn=b j =a, j =b, r =r(j).
В каждой части произвольным образом выбираем точку Ci и вычисляем в ней значение ri =r(Ci) угол i- части Просуммируем площади всех круговых секторов Сумма этих площадей приближенно равна площади исходного криволинейного сектора. Причем, чем больше будет частей разбиения, тем меньше будет Dji , тем точнее будет равенство.
Вычисление длины дуги кривой в декартовой системе координат. Нужно вычислить длину плоской кривой L, заданной уравнением y=f(x) на отрезке [a,b]. Разобьем отрезок на части точками xi где I=0…n, a=x0<x1<x2<…<xn=b. Через эти точки проведем прямые параллельные оси OY, которые разобьют кривую на M частей. Выпишем в эти части ломанную. Длина I-ого звена ломанной: Dli= Просуммируем
Пример: Вычислить длину полукубической параболы
Вычисление длины дуги в полярной системе координат и кривой заданной параметрически. В декартовой системе координат длина дуги L= Если кривая L задана параметрически.
Длина кривой заданной параметрически, выражается через определенный интеграл L= Замечание: При вычислении длины кривой заданной параметрически нижний предел интегрирования должен быть меньше верхнего предела интегрирования.
L= =8 (ед) Если кривая L задана в полярной системе координат
= = Длина дуги кривой в полярной системе координат L= Пример: Вычислить длину кардиоиды = = ½L= Объем тела через площадь поперечного сечения. Пусть дано некоторое тело и известно, что площадь поперечного сечения плоскости перпендикулярна оси OX. Разобьем тело на части плоскостями x=xi перпендикулярными оси OX. Отрезок [a,b], лежащий на оси OX, разобьется соответственно точками xi на n частей: a=x0<x1<x2<…<xn=b. Dxi = xi+1 – xi - длина [xi ; xi+1]. В каждой точке x принадлежащей отрезку [a,b] известно поперечное сечение этого тела, то есть площадь поперечного сечения является функцией от x(S(x)). На i отрезке выберем произвольную точку Ci и заменим объем i части тела объемом прямого цилиндра Vi = Sосн × высоту=S(Ci) × Dxi ; объем тела приближенно равен сумме объемов прямых цилиндров VT »
Объем тела вращения. Определение: Если криволинейная трапеция ограничена линиями y=0; x=a; x=b; y=f(x), где f(x)³0 вращается вокруг оси OX, то полученное тело называется телом вращения вокруг оси OX. Как известно, объем тела выражается через площадь поперечного сечения по формуле: Замечание: Если фигура не является криволинейной трапецией, то ее нужно разбить на нужные части, либо достроить нужные части и вычислять объем тела вращения, как неполый через сумму или разность объемов частей. Пример: Вычислить объемы тел вращения, ограниченного линиями y=0; x=0; x=1; y=ex.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 . Заменим площадь i- части площадью кругового сектора
. Заменим площадь i- части площадью кругового сектора 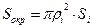 = =
= =  =
=  =
= 
 .
. В ПСК S=
В ПСК S=  .
.

 сумма длин звеньев ломанной приближенно равна длине кривой. Переходя к пределу:
сумма длин звеньев ломанной приближенно равна длине кривой. Переходя к пределу:  =
=  =
= 


 , где
, где 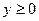 , x=0, x=1.
, x=0, x=1. 

 = =
= =  =
= 

 . Рассмотрим подынтегральное выражение
. Рассмотрим подынтегральное выражение  внесем dx под корень
внесем dx под корень  - это выражение называется дифференциалом дуги.
- это выражение называется дифференциалом дуги.  .
.
 =
=  =
= 


 .
. Пример: Найти длину 1 арки циклоиды.
Пример: Найти длину 1 арки циклоиды.

 =
= 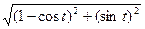 =
=  =
=  =
=  =
=  =
=  ==
== 
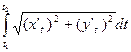 =
=  =
=  =
=  =-4(-1-1)=
=-4(-1-1)=

 =
= 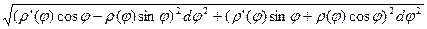 =
= =
=

 . В силу симметричности кривой вычислим ½ длины. Полярный угол
. В силу симметричности кривой вычислим ½ длины. Полярный угол 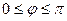 ½L=
½L= 
 =
=  =
=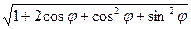 =
=  =
=  =
=  =
= =
= 
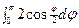 =
=  =4(1-0)=4 Þ L=4*2=8 (ед).
=4(1-0)=4 Þ L=4*2=8 (ед). ; Причем равенство будет тем точнее, чем больше частей разбиения тела и чем меньше длина отрезка Dxi . Переходя к пределу получаем VT=
; Причем равенство будет тем точнее, чем больше частей разбиения тела и чем меньше длина отрезка Dxi . Переходя к пределу получаем VT=  . Этот предел интегральных сумм является определенным интегралом
. Этот предел интегральных сумм является определенным интегралом  где S(x) – площадь поперечного сечения.
где S(x) – площадь поперечного сечения. . Если криволинейная трапеция ограниченная линиями
. Если криволинейная трапеция ограниченная линиями  вращается вокруг оси OY, то объем полученного тела вращения VOY=
вращается вокруг оси OY, то объем полученного тела вращения VOY= 

