|
|
Вычисление площади плоской фигурыПервообразная функция и неопределённый интеграл Определение. Функция ПРИМЕР. Функция Замечание. Если функция Определение. Неопределённым интегралом от функции
здесь Определение. Нахождение первообразной или неопределённого интеграла называется интегрированием. Свойства неопределённого интеграла: 1) 2) 3) 4)
Таблица основных интегралов Таблица содержит формулы, легко проверяемые непосредственным дифференцированием.
Основные методы интегрирования а) Метод непосредственного интегрирования – состоит в том, чтобы данный интеграл привести к табличному интегралу. ПРИМЕРЫ. 1)
2) 3) 4) 5)
б) Замена переменной интегрирования – состоит в том, что вводится новая переменная интегрирования, которая позволяет привести данный интеграл к табличному интегралу. ПРИМЕР.
в) Интегрирование по частям – Замечания. Пусть 1) 2) 3) 4) 5) ПРИМЕР.
тема 2. Интегрирование рациональных дробей Рациональные дроби Определение. Рациональной дробью называется функция, равная отношению двух многочленов:
где Определение. Рациональная дробь называется правильной (неправильной), если степень многочлена, стоящего в числителе, меньше (больше или равна) степени многочлена, стоящего в знаменателе:
ПРИМЕРЫ.
Неправильную дробь всегда можно свести к правильной, разделив числитель на знаменатель «столбиком» и выделив из дроби целую часть (многочлен). Всякую правильную рациональную дробь можно представить в виде суммы конечного числа так называемых простейших дробей следующих четырёх типов: I. II. III. IV. где трёхчлен Интегрирование простейших рациональных дробей ПРИМЕРЫ. I. II. III.
Разложение правильной рациональной дроби на простейшие Теорема. Если знаменатель правильной рациональной дроби то справедливо следующее разложение дроби на сумму простейших дробей: где Таким образом, интеграл от правильной рациональной дроби ПРИМЕР. Представить дробь в виде суммы простых дробей.
Одним из наиболее простых методов определения коэффициентов в разложении правильной дроби на простейшие является метод неопределённых коэффициентов.
тема 3. Интегрирование некоторых иррациональных функций
1) Если подынтегральное выражение содержит лишь линейную иррациональность
ПРИМЕР. 2) Если подынтегральное выражение содержит несколько радикалов
ПРИМЕР.
3) Интегралы с помощью дополнения квадратного трёхчлена
ПРИМЕР.
тема 4. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Определённый интеграл Определение. Криволинейной трапецией называется часть плоскости, ограниченная графиком функции Определенный интеграл функции a и b – пределы интегрирования (a – нижний предел, b – верхний предел). Геометрический смысл определенного интеграла: если функция Свойства определённого интеграла: 1) 2) 3) 4) 5) 6) Если функции 7) если 8) если 2) Формула Ньютона–Лейбница:
ПРИМЕР.
3) Интегрирование по частям в определённом интеграле: ПРИМЕР.
тема 5. ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА Вычисление площади плоской фигуры Теорема 1. Если функция Замечание. Если Теорема 2. Если плоская фигура ограничена на отрезке
Теорема 3. Если функция
ПРИМЕР. Вычислить площадь фигуры, ограниченной кривыми По теореме 2 имеем
Пусть дуга Определение. Длиной дуги Длина Вычисление объёмов тел Объём тела вычисляется по формуле тема 6. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ ПЕРВОГО РОДА
Определение. Несобственными интегралами первого рода называются интегралы с одним бесконечным пределом интегрирования, которые определяются по формулам
Определение. Если при Расходящемуся интегралу не приписывают никакого числового значения. ПРИМЕРЫ. 1) 2) Определение. Несобственным интегралом в пределах от
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
называется первообразной для данной функции 
, если выполняется равенство 
.
является первообразной функции 
на всей числовой прямой R, так как 
справедливо 
.
, где 
, 
, также является первообразной для функции 
,
,
,
,
.
, 
, 
.
.
.
.
.
.
.
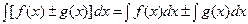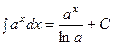
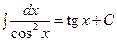
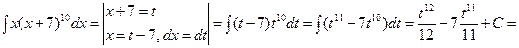
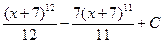– многочлен n-й степени от х. Тогда в интегралах
лучше принять 
, здесь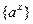 
– показательные функции;
лучше принять 
– тригонометрические функции;
лучше принять 
, здесь 
– логарифмические функции;
лучше принять 
, здесь 
– обратные тригонометрические функции;
, 
лучше принять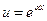 
.
.
,
, 
– многочлены степени n и m соответственно.
– правильная рациональная дробь; 
– неправильная рациональная дробь.
, 
– постоянные действительные числа,
не имеет действительных корней, то есть 
.
.
.
.
разлагается на множители в виде:
, 
,
– постоянные действительные числа.
.
( 
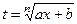), то полезна подстановка
.
.
, 
, …, 
, то полезна подстановка
, m=НОК(m1, m2, …, ms).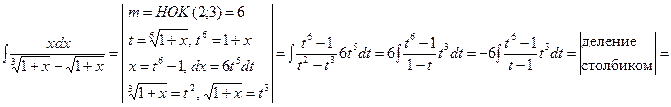
…
и 
до полного квадрата приводятся в зависимости от знака коэффициента А к одному из двух табличных интегралов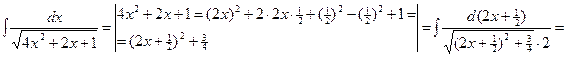
.
, осью Ох ( 
) и отрезками прямых 
, 
.
: 
,
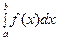геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции 
, с боков – отрезками прямых 
,
,
, 
,
,
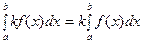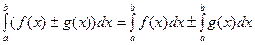, где 
,
( 
) на 
, то 
,
, то 
,
.
,
.
.
.
и непрерывна на отрезке 
.
на 
.
и 
, причем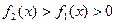 
, то площадь S этой фигуры вычисляется по формуле
.
, 
и кривая 
.
и 
на 
.
.
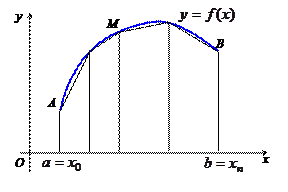2) Вычисление длины дуги плоской кривой
задана уравнением 
.
дуги кривой 
.
, где S(x) – площадь сечения тела плоскостью, перпендикулярной оси Ох, a и b – пределы изменения переменной х для произвольной точки тела.
, (1)
. (2)
( 
) существует конечный предел в формуле (1) ((2)), то говорят, что несобственный интеграл сходится. Если при 
. Следовательно, данный интеграл расходится.
. Следовательно, данный интеграл сходится.
до 
называется интеграл
, 
.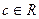