
|
|
Свойства определённого интегралаИнтегрирование функции одной переменной Неопределенный интеграл В дифференциальном исчислении мы решаем следующую основную задачу – нахождение производной по заданной функции. В интегральном исчислении решается обратная задача: поиск функции, производная которой известна. По данной функции f(x) будем искать такую функцию F(x), производная от которой равняется заданной: для f(x) найти F’(x) = f(x). Или, для данной функции f(x) найти такую F(x), что её дифференциал dF(x) = f(x)dx.
ОПРЕДЕЛЕНИЕ: Функция F(X) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений х на этом промежутке производная функции F(X) равна f(x). ( Пример. F(x) = sinx является первообразной для функции f(x) = cosx. F(x) = x3 – первообразная для f(x) = 3x2; F(x) = Если функция непрерывна на отрезке, то у нее существует первообразная. Задача отыскания по данной функции f(x) ее первообразной F(x) решается неоднозначно. ТЕОРЕМА. Если СЛЕДСТВИЕ. Если F(x) первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для этой функции может быть представлена виде F(x) + C.
ОПРЕДЕЛЕНИЕ: Неопределенный интегралом данной непрерывной функции f(x) на некотором промежутке X называется множество всех первообразных для данной функции.
где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, dx – дифференциал аргумента интеграла, F(x) – первообразная подынтегральной функции, С – постоянное слагаемое.
Геометрический смысл. F(x)+C1 Неопределенный интеграл представляет собой семейство кривых, получающихся путем сдвига F(x) одной из них (графика функции параллельно самой себе вдоль оси OY. Х Свойства неопределенного интеграла:
1. Производная неопределенного интеграла равна подынтегральной функции. (∫ f(x)dx) ´ = f(x) Доказательство: ( ∫ f(x)dx)´ = (F(x) + C)’ = 2. Дифференциал от неопределенного интеграла равен подинтегральному выражению. d(∫ f(x)dx) = f(x)dx. Доказательство: d( ∫ f(x)dx ) = d( F(x) + C) = ( F(x) + C )’dx = f(x)dx 3.Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной. ∫ d u(x) = u(x) + C В частности, 4. Постоянный ненулевой множитель подынтегральной функции может быть вынесен за знак интеграла Если А ≠ 0, А = const, то ∫ А f(x)dx = А∫ f(x)dx 5. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме неопределенных интегралов от этих функций.
Используя основные методы интегрирования, можно получить ещё несколько формул для вычисления часто встречающихся интегралов:
Каждая из формул интегрирования остается инвариантной (неизменной), если переменные интегрирования х заменить любой дифференцируемой функцией. Определённый интеграл. Криволинейная трапеция – фигура, ограниченная сверху- графиком функции y = f(x), снизу - осью Ox, сбоку - прямыми x = a, x = b. Определённый интеграл функции y = f(x) на отрезке интегрирования [a; b] – это число, равное площади криволинейной трапеции S.
Свойства определённого интеграла 1) Если f(x) интегрируема на отрезке [a; b], то функция A· f(x) также интегрируема на [a; b] и
2) Если f(x) и g (x) интегрируемы на отрезке [a; b], то интеграл сумма этих функций равен сумме интегралов.
3) Если верхний и нижний пределы интегрирования равны между собой, то определённый интеграл равен нулю.
4) При перемене местами верхнего и нижнего пределов интегрирования определённый интеграл меняет знак на противоположный.
5) Свойство аддитивности. Свойства монотонности. 6) Если a < b, f (x) ≥ 0, то определённый интеграл: 7) Если для любого x Î [a; b] f (x) ≥ g (x), то: Оценочные свойства. 8) Если существует определённый интеграл 9) Если для "x Î [a; b] m ≤ f (x) ≤ M, тогда: Теорема о среднем: Приложение определённого интеграла. 1. площадь криволинейной трапеции.
2. Чтобы найти x0, нужно решить уравнение:
3. Объем тела, образовавшегося вращением, криволинейной трапеции вокруг осей

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 выполняется равенство F’(x) = f(x))
выполняется равенство F’(x) = f(x)) - является первообразной для функции f(x) =
- является первообразной для функции f(x) = 
 и
и  первообразные от функции f(x) на некотором промежутке X, то для всех значений х на этом промежутке они отличаются друг от друга на постоянное слагаемое.
первообразные от функции f(x) на некотором промежутке X, то для всех значений х на этом промежутке они отличаются друг от друга на постоянное слагаемое.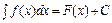
 Y F(x)+C2
Y F(x)+C2 )
)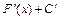 = f(x)+0=f(x)
= f(x)+0=f(x) . (Интегрирование и дифференцирование – обратные операции)
. (Интегрирование и дифференцирование – обратные операции)

 xmdx = xm+1/m+1 + C
xmdx = xm+1/m+1 + C


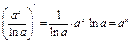
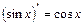




 +С
+С

 +С
+С








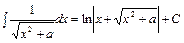
 , где a и b – нижний и верхний пределы интегрирования
, где a и b – нижний и верхний пределы интегрирования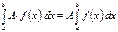





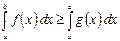
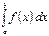 , то
, то 
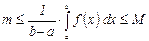
 ,
, 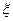 Î [a; b]
Î [a; b]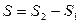



 Площадь трапеции, ограниченной сверху различными функциями.
Площадь трапеции, ограниченной сверху различными функциями. 




