
|
|
Теория статистики: Учебник/ Под ред проф. Громыко Г.Л. М.-ИНФРА-М,2000-414сВыполнения Указания о порядке выполнения контрольных работ
1. Задания к контрольной работе составлены в семи вариантах, выбор которого зависит от начальной буквы фамилии студента.
2. Каждый вариант контрольной работы включает 12 задач по наиболее важным разделам курса. 3. Контрольные задания необходимо выполнять последовательно, так как указаны номера задач, после проработки методических указаний по их решению и соответствующей литературы. Перед решением нужно полностью привести условия задачи. 4. Работы могут быть выполнены как в компьютерном варианте, так и в письменном виде в отдельной тетради или на листах формата А-4, написаны чернилами и аккуратно оформлены (разборчивый почерк, оставление полей, систематизацию данных в таблицах и т. д.). 5. Решение задач следует сопровождать необходимыми формулами, краткими пояснениями, расчетами. Задачи, в которых даны только ответы будут считаться переписанными. 6. Все расчеты относительных показателей надо приводить с точностью до 0,001, а проценты — до 0,01. 7. По каждому исчисленному экономическому показателю необходимо писать выводы и пояснения. 8. Страницы работы должны быть пронумерованы, иметь список использованной литературы, подпись и дату. Задания к контрольным работам Вариант №1 Задача 1.
Имеются следующие данные о работе 24-х заводов одной из отрасли промышленности:
Для обобщения результатов представленных данных постройте ряд распределения заводов по стоимости основных производственных фондов, образовав пять групп с равными интервалами. Вычислите удельные веса заводов в каждой группе. Укажите наиболее характерную величину основных производственных фондов отрасли. Сделайте выводы. Задача 2. За отчетный период предприятие израсходовало на производственные нужды следующее количество тонн условного топлива:
Определите общее количество потребленного в отчетном периоде топлива. Задача 3. По данным о пассажирообороте всех видов транспорта общего пользования в России (млрд. пассажиро-км) вычислите относительные величины структуры пассажирооборота за 2001-2002 гг.:
Результаты вычислений представьте в виде таблицы и проанализируйте полученные данные. Задача 4.
Две бригады рабочих обрабатывают один и тот же вид деталей. Дневная выработка деталей отдельными рабочими характеризуется следующими данными (цифры условные):
Определите: среднее дневное число деталей, обработанных одним рабочим каждой бригады за 1 день, и дайте сравнительную характеристику этих средних; среднее число деталей, обработанных двумя бригадами за день.
Задача 5.
Методом собственно случайной величины обследована жирность молока у 100 коров. По данным выборки средняя жирность молока оказалась равной 3,64%, а дисперсия составила 2,56. Определить: а) среднюю ошибку выборки; б) с вероятностью, равной 0,954, предельные значения генеральной средней.
Задача 6.
Имеются данные об оплате труда на одном из предприятий:
Рассчитайте: 1) среднемесячную заработную плату; 2) моду; 3) медиану; 4) дисперсию; 5) среднеквадратическое отклонение; 6) коэффициент вариации.
Задача 7.
Имеются следующие данные о производстве зерна (млн. т.) в одной из областей РФ за ряд лет:
Определить: 1. Абсолютные приросты. 2. Цепные темпы роста. 3. Цепные темпы прироста. 4. Абсолютное значение 1% прироста. Задача 8.
Динамика производства зерна в 1998-2002 гг. характеризуется следующими показателями:
На основе этих данных, исчислите: 1. Средний уровень ряда. 2. Среднегодовой темп роста и прироста. 3. Среднегодовой абсолютный прирост.
Задача 9.
До 1997 года в состав производственного объединения входило 20 предприятий. В 1997 году в него влилось еще 4 предприятия. Произведите смыкание ряда динамики двумя методами, используя следующие данные:
Приведите уровни ряда динамики к сопоставимому виду двумя методами.
Задача 10.
Имеются данные о производстве и ценах продукции:
Рассчитайте индексы: 1) физического объема и цен по каждому виду продукции; 2) физического объема и цен по всем видам продукции; 3) стоимости продукции. Используя взаимосвязь индексов,произведите анализ: 1) динамики стоимости продукции в целом и за счет факторов; 2) абсолютного прироста продукции в целом, а также за счет: изменения цен, изменения объема продукции.
Задача 11.
На основе имеющихся данных о стоимости произведенной продукции и индексах физического объема и цен рассчитать среднеарифметический индекс объема и среднегармонический индекс цен.
Задача 12. Себестоимость и объем продукции заводов характеризуются следующими данными:
Проанализируйте динамику изменения средней себестоимости, рассчитайте индексы переменного, постоянного состава и структурных сдвигов. В анализе используйте наряду с относительными и абсолютные показатели.
Вариант №2 Задача 1. Имеются следующие данные о работе 24-х заводов одной из отрасли промышленности:
Постройте ряд распределения заводов по среднесписочной численности работающих, образовав четыре группы рабочих с равными интервалами. В каждой группе подсчитайтеудельный вес заводов по численности работающих. Сделайте выводы. Задача 2. За отчетный период предприятие израсходовало на производственные нужды следующее количество тонн условного топлива:
Определите общее количество потребленного в отчетном периоде топлива.
Задача 3.
По приведенным ниже данным о средней годовой численности работников в промышленности (тыс. чел.) вычислите: а) относительные величины структуры промышленно-произвоственного персонала за 2001-2002 гг.; б) относительные величины динамики всего промышленно-производственного персонала и каждой категории персонала в 2002 г. по сравнению с 2001 г.:
Задача 4.
Урожайность и посевные площади зерновых культур характеризуются данными таблицы (цифры условные):
Определите среднюю урожайность зерновых культур по колхозу. Какую формулу средней вы применили при решении задачи? Что в задаче является варьирующим признаком, весами? Какой показатель стоит в числителе средней?
Задача 5.
На основе выборочного метода обследовано 600 рабочих (n = 600) в отрасли установлено, что удельный вес численности женщин составил 0,4 (W = 0,4). С какой вероятностью можно утверждать, что при определении доли женщин, занятых в этой отрасли, допущена ошибка (∆), не превышающая 5% (0,05).
Задача 6.
Имеются следующие данные о распределении населения страны по размеру среднедушевого дохода в месяц:
Рассчитайте: 1) среднедушевой доход; 2) моду; 3) медиану; 4) дисперсию; 5) среднеквадратическое отклонение душевого дохода; 6) вариацию.
Задача 7.
Имеются следующие данные о производстве газа в одном из регионов за 1996-2002 гг. (млн. т.), данные условные:
Определить: 1. Абсолютные приросты. 2. Цепные темпы роста. 3. Цепные темпы прироста. 4. Абсолютное значение 1% прироста.
Задача 8.
Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным о производстве продукции предприятиями объединения:
Задача 9.
Имеются следующие данные о поголовье крупного рогатого скота в хозяйствах всех категорий области (тыс. голов):
Приведите уровни ряда динамики к сопоставимому виду двумя методами.
Задача 10.
Имеются данные о производстве и ценах продукции:
Рассчитайтеиндексы: 1) физического объема и цен по каждому виду продукции; 2) физического объема и цен по всем видам продукции; 3) стоимости продукции. Используя взаимосвязь индексов, произведите анализ: 1) динамики стоимости продукции в целом и за счет факторов; 2) абсолютного прироста продукции в целом, а также за счет: изменения цен, изменения объема продукции.
Задача 11.
На основе имеющихся данных о стоимости произведенной продукции и индексах физического объема и цен рассчитать среднеарифметический индекс объема и среднегармонический индекс цен.
Задача 12.
Себестоимость и объем продукции заводов характеризуются следующими данными:
Проанализируйте динамику изменения средней себестоимости, рассчитайте индексы переменного, постоянного состава и структурных сдвигов. В анализе используйте наряду с относительными и абсолютные показатели.
Вариант №3 Задача 1. Имеются следующие данные о работе 24-х заводов одной из отрасли промышленности:
Постройте ряд распределения заводов по проценту выполнения плана выпуска товарной продукции, образовав следующие группы: а) не выполнившие план; б) выполнившие план на 100—105%, 105—115%, свыше 115%. Выделенные группы охарактеризуйтеабсолютными и относительными показателями. Сделайте выводы. Задача 2. Используя метод условно-натурального измерения, определите в целом по всем видам продукции: а) величину планового задания; б) степень выполнения планового задания; в) динамику производства продукции.
Задача 3. Удельный вес посевных площадей зерновых культур колхоза в его общей посевной площади составил в 1996 году 75,4 %, а удельный вес пшеницы в общей посевной площади колхоза — 34,6 %. Определите удельный вес посевных площадей пшеницы в посевной площади зерновых. Задача 4.
Средняя месячная выработка шелковых тканей рабочих трех бригад и их средняя численность за месяц составили (цифры условные):
Определите среднюю месячную выработку шелковых тканей рабочими ткацкой фабрики в целом за месяц.
Задача 5.
Сколько сотрудников предприятию надо обследовать в порядке случайной выборки, чтобы с вероятностью (Р), равной 0,954, можно было гарантировать ошибку не более 75 руб.? Предполагаемое среднее квадратическое отклонение заработной платы
Задача 6.
На один из периодов года в стране имелось следующее распределение безработных по возрастным группам:
Рассчитайте: 1) средний возраст безработных; 2) моду; 3) медиану; 4) среднеквадратическое отклонение; 5) коэффициент вариации.
Задача 7.
Ввод в действие жилых домов предприятиями всех форм собственности в одном из регионов в 1995-2002 гг. характеризуется следующими данными (млн. кв. м. общей площади):
На основе этих данных исчислите: 1. Средний уровень ряда. 2. Среднегодовой темп роста и прироста. 3. Среднегодовой абсолютный прирост. Задача 8.
По данным о пассажирообороте автобусного транспорта региона вычислите недостающие показатели динамики:
Задача 9.
Имеются следующие данные о валовом сборе овощей в регионе:
Приведите уровни ряда динамики к сопоставимому виду двумя методами.
Задача 10.
Имеются данные о производстве и ценах продукции:
Рассчитайте индексы: 1) физического объема и цен по каждому виду продукции; 2) физического объема и цен по всем видам продукции; 3) стоимости продукции. Используя взаимосвязь индексов, произведите анализ: 1) динамики стоимости продукции в целом и за счет факторов; 2) абсолютного прироста продукции в целом, а также за счет: изменения цен, изменения объема продукции.
Задача 11.
На основе имеющихся данных о стоимости произведенной продукции и индексах физического объема и цен рассчитать среднеарифметический индекс объема и среднегармонический индекс цен.
Задача 12.
Себестоимость и объем продукции заводов характеризуются следующими данными:
Для двух заводов проанализируйте динамику изменения средней себестоимости, рассчитайте индексы переменного, постоянного состава и структурных сдвигов. В анализе используйте наряду с относительными и абсолютные показатели.
Вариант №4 Задача 1. Имеются следующие данные о работе 24-х заводов одной из отрасли промышленности:
Произведите группировку заводов по численности работающих, образовав четыре группы с равными интервалами. По каждой группе подсчитайте: 1) число заводов; 2) число работающих — всего и в среднем на один завод; 3) размер продукции — всего и в среднем на один завод; 4) размер продукции на одного работающего. Результаты представьте в таблице. Дайте анализ полученных показателей. Задача 2.
За отчетный период предприятие выработало следующее количество моющих средств по видам:
Определите общее количество продукции, выработанной предприятием. Задача 3.
Численность студентов института по формам обучения и полу характеризуется таблицей (цифры условные):
Определите по этим данным: а) удельный вес студентов — мужчин и женщин, обучающихся по каждой из трех форм обучения и всем трем формам обучения в целом (столбцовые удельные веса), в общей численности студентов, обучающихся по каждой форме обучения; б) удельный вес студентов (мужчин, женщин и общей численности), обучающихся по каждой из трех форм обучения, в общей численности мужчин и женщин и всех студентов (строчные удельные веса); в) удельный вес студентов (мужчин и женщин), обучающихся по одной из трех форм обучения в общей численности всех студентов института (комбинированные удельные веса). Представьте вычисленные вами данные в виде таблицы. Проанализируйте эти данные. Задача 4.
По четырем цехам завода известны следующие данные о средней заработной плате работающих и их численности за месяц:
Определите среднюю заработную плату работающих по заводу в целом за месяц. Какое свойство средней арифметической вы использовали при решении этой задачи?
Задача 5.
Средняя продолжительность горения, установленная путем испытания 15 случайно отобранных электрических лампочек (n), оказалась равной 1250 часов при среднем квадратическом отклонении 20 часов. С какой вероятностью можно утверждать, что допущенная при этом предельная ошибка выборки (т. е. расхождение между выборочной и генеральной средней) не превысит 18 часов?
Задача 6.
На один из периодов года в стране имелось следующее распределение безработных по возрастным группам:
Рассчитайте: 1) средний возраст безработных; 2) моду; 3) медиану; 4) среднеквадратическое отклонение; 5) коэффициент вариации.
Задача 7.
Имеются следующие данные по России о вводе в действие жилой площади за 1997-2002 гг.:
На основе этих данных вычислите: 1. Средний уровень ряда. 2. Среднегодовой темп роста и прироста. 3. Среднегодовой абсолютный прирост.
Задача 8.
По данным о речных перевозках вычислите недостающие показатели динамики:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
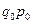
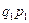

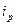
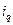
 = 150 руб.
= 150 руб.