
|
|
Интегрирование тригонометрических выражений.12 Пусть 1-й случай. Интеграл С учетом сделанной замены получим где Пример: Найти неопределенный интеграл: Решение: Сделаем универсальную тригонометрическую подстановку:
Тогда Последний интеграл вычислим отдельно. Для этого выделим полный квадрат в знаменателе дроби:
Воспользовавшись заменой переменной
Окончательно находим:
Отметим, что универсальную тригонометрическую подстановку, как правило, используют в тех случаях, когда другие подстановки, приведенные ниже не приводят к желаемым результатам. 2-й случай. В интегралах
Этой же подстановкой к интегралам от рациональных функций приводятся интегралы вида Пример: Найти неопределенный интеграл:
Решение: Сделаем подстановку:
Тогда
Пример. Найти неопределенный интеграл: Решение:
Интегрирование выражений вида
где mи n-целые числа. Рассмотрим два случая: 1-й случай. Среди чисел m,nесть хотя бы одно нечетное. Тогда за tпринимается функция, стоящая в основании другой степени. Задача. Найти неопределенный интеграл:
Решение: Здесь функция sinxстоит в нечетной степени, поэтому
2-й случай. В выражении (6) оба числаm,n- четные неотрицательные. Положим m=2p, n=2q и применим формулы:
Тогда Раскрыв скобки, получим сумму интегралов, к каждому из которых применим 1-й или 2-й способы:
1.10 Определенный интеграл: задача о площади криволинейной трапеции Задача. Определение: Криволинейной трапецией называется фигура, ограниченная линейно x=a; x=b; y=0; y=f(x)³0
В каждом отрезке выберем произвольную точку Ci Î[ xi, xi-1] и вычислим в ней значение функции f(Ci). Заменим площадь i-й части криволинейной трапеции площадью прямоугольника с основанием
Причем равенство будет тем точнее, чем больше количество отрезков или чем меньше их длина.
1.11 Определение определенного интеграла. Пусть функция y=f(x)определена на отрезке [a,b]. Разобьем отрезок [a,b] на части точками a=x0<x1<x2<…<xn=b. Обозначим через Dxi=xi – xi-1 . В каждом из отрезков возьмем точку Ci Î[ xi -1, xi] и вычислим в ней значение функции f(Ci). Составим интегральную сумму Sn= Теорема о существовании определенного интеграла. Если функция y=f(x) непрерывна на отрезке [a,b], то существует определенный интеграл Замечание: Определенный интеграл всегда является числом. Определенный интеграл зависит от a, от b, от f(x) и не зависит от переменной интегрирования.
1.12Свойства определенного интеграла.
1.13Интеграл с переменным верхним пределом и его производная. Интегралом с переменным верхним пределом называется интеграл от a до x по dx, где нижний предел число, а верхний предел – переменная интегрирования. Теорема: Производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела (при условии, что подынтегральная функция непрерывна). Ñ Возьмем точку x и вычислим в ней значение функции J(x)= Функция I(x) получает приращение DI=I(x+Dx) – I(x)= По теореме о среднем значении существует точка C Î(x,x+Dx), такая что
Из теоремы следует, что интеграл с переменным верхним пределом является одной из первообразных подынтегральной функции.
1.14Формула Ньютона-Лейбница.
Рассмотрим Формула позволяет вычислять определенный интеграл. Пример:
= 1.15Интегрирование по частям и замена переменной в определенном интеграле. Интегрирование по частям.
Например: Интегрирование с заменой переменной.
Замечание: При замене переменной в определённом интеграле нужно поменять пределы интегрирования, причем решения уравнений При замене переменной в определенном интеграле возвращаться к старой переменной не нужно. Пример:
Рассмотрим криволинейную трапецию, ограниченную прямыми x=a, x=b, y=0 и кривой y=f(x), где f(x) ³ 0.
Пример: Вычислить площадь фигуры, ограниченной линиями y=e2x, x=0, x=2, y=0. S=
Пример: Вычислить площадь фигуры, ограниченной линиями y=x, xy=1(y=1/x), x=0, x=2, y=0. Разобьем трапецию на две части S1 и S2. Площадь всей трапеции: S=S1+S2=
В этом случае, неважно, где лежит криволинейная трапеция, выше оси OX или ниже, или часть выше, часть ниже. Самое главное, чтобы выполнялось f2(x) ³ f1(x). 1.17 Вычисление площадей при параметрическом задании функции. Пусть криволинейная трапеция ограничена линиями x=a, x=b, y=0, а верхняя граница задана параметрически Пример: Вычислить площадь эллипса. Параметрические уравнения эллипса В силу симметричности фигур вычислим 1/4 площади. Для этой части x меняется от 0 до a. Найдем пределы интегрирования. 0 = a cos t, cos t = 0, t1=p/2 a = a cos t, cos t = 1, t2 = 0
Итак,
1.18Полярная система координат.
Таким образом любая точка в полярной системе координат будет иметь две координаты M(r,j), r – полярный радиус, j – полярный угол. Очевидно, что r – величина неотрицательная (как длина любого вектора), а угол j может быть любой. Если угол j измерен против часовой стрелки, то его будем считать положительным, если по часовой стрелке, то отрицательным. Изображение линий в полярной системе координат. r= R – окружность с центром в полюсе и радиусом R. j= a - луч под углом r= j – при построении любой кривой в полярной системе координат, нужно задавать различные значения полярного угла j и вычислять соответственно значения полярного радиуса r. Если r получится меньше нуля, то картинки не будет (этой части рисунка не будет)
Связь между декартовой и полярной системами координат. Если полярную и декартову систему координат совместить так, чтобы полюс совпал с началом координат, а полярная ось с положительным направлением оси 0x, то можно получить формулы перехода от полярных координат (r; j) к декартовым (x; y):
1.19Вычисление площади в полярной системе координат и кривой заданной параметрически. Если в декартовой системе координат вычисляется площадь криволинейной трапеции, то в полярной системе вычисляется площадь криволинейного сектора. Определение: Криволинейным сектором называется фигура, заключенная между двумя лучами, выходящими из полюса под углами j=a и j=b и кривой, заданной в полярной системе координат r=r(j). Разобьем криволинейный сектор лучами j=j i, i = 0…n на части a=j0 <j1<j2<…<jn=b j =a, j =b, r =r(j).
В каждой части произвольным образом выбираем точку Ci и вычисляем в ней значение ri =r(Ci) угол i- части Просуммируем площади всех круговых секторов Сумма этих площадей приближенно равна площади исходного криволинейного сектора. Причем, чем больше будет частей разбиения, тем меньше будет Dji , тем точнее будет равенство.
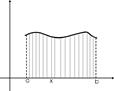
1.20Вычисление длины дуги кривой в декартовой системе координат. Нужно вычислить длину плоской кривой L, заданной уравнением y=f(x) на отрезке [a,b]. Разобьем отрезок на части точками xi где I=0…n, a=x0<x1<x2<…<xn=b. Через эти точки проведем прямые параллельные оси OY, которые разобьют кривую на M частей. Выпишем в эти части ломанную. Длина I-ого звена ломанной: Dli= Просуммируем
Пример: Вычислить длину полукубической параболы
1.21Вычисление длины дуги в полярной системе координат и кривой заданной параметрически. В декартовой системе координат длина дуги L= Если кривая L задана параметрически.
Длина кривой заданной параметрически, выражается через определенный интеграл L= Замечание: При вычислении длины кривой заданной параметрически нижний предел интегрирования должен быть меньше верхнего предела интегрирования.
L= =8 (ед) Если кривая L задана в полярной системе координат
= = Длина дуги кривой в полярной системе координат L= Пример: Вычислить длину кардиоиды = = ½L= 1.22Объем тела через площадь поперечного сечения. Пусть дано некоторое тело и известно, что площадь поперечного сечения плоскости перпендикулярна оси OX. Разобьем тело на части плоскостями x=xi перпендикулярными оси OX. Отрезок [a,b], лежащий на оси OX, разобьется соответственно точками xi на n частей: a=x0<x1<x2<…<xn=b. Dxi = xi+1 – xi - длина [xi ; xi+1]. В каждой точке x принадлежащей отрезку [a,b] известно поперечное сечение этого тела, то есть площадь поперечного сечения является функцией от x(S(x)). На i отрезке выберем произвольную точку Ci и заменим объем i части тела объемом прямого цилиндра Vi = Sосн × высоту=S(Ci) × Dxi ; объем тела приближенно равен сумме объемов прямых цилиндров VT »
Объем тела вращения. Определение: Если криволинейная трапеция ограничена линиями y=0; x=a; x=b; y=f(x), где f(x)³0 вращается вокруг оси OX, то полученное тело называется телом вращения вокруг оси OX. Как известно, объем тела выражается через площадь поперечного сечения по формуле: Замечание: Если фигура не является криволинейной трапецией, то ее нужно разбить на нужные части, либо достроить нужные части и вычислять объем тела вращения, как неполый через сумму или разность объемов частей. Пример: Вычислить объемы тел вращения, ограниченного линиями y=0; x=0; x=1; y=ex.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 - рациональная функция своих аргументов. Рассмотрим несколько случаев:
- рациональная функция своих аргументов. Рассмотрим несколько случаев: универсальной тригонометрической подстановкой
универсальной тригонометрической подстановкой 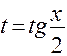 сводится к интегралу от рациональной функции. При этом
сводится к интегралу от рациональной функции. При этом  .
.
 ,
, - рациональная функция, интеграл от которой рассматривался выше.
- рациональная функция, интеграл от которой рассматривался выше. .
. .
. .
.


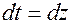 получим
получим
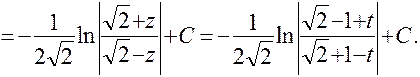
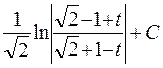 =
=  .
. , где
, где  и
и  входят в подынтегральную рациональную функцию, только в четных степенях делается замена
входят в подынтегральную рациональную функцию, только в четных степенях делается замена  . При этом
. При этом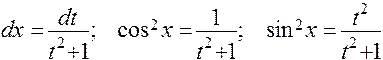 .
. .
.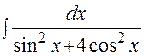 .
.
 .
. .
.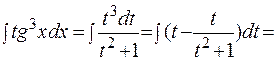

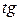

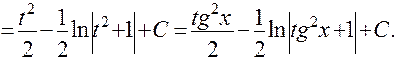
 , (6)
, (6) .
.

 ;
; .
.


 .
.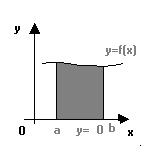
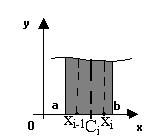 Разобьем основание криволинейной трапеции отрезок [a,b] на n частей точками a=x0<x1<x2<…<xn=b. Обозначим через Dxi=xi – xi-1 длину i-го отрезка.
Разобьем основание криволинейной трапеции отрезок [a,b] на n частей точками a=x0<x1<x2<…<xn=b. Обозначим через Dxi=xi – xi-1 длину i-го отрезка. и высотой f(Ci):
и высотой f(Ci):  ;
; .
. . Если существует предел интегральных сумм, при max Dxi ®0, которые не зависят от способа разбиения отрезка [a,b] на части и способа выбора точек Ci, то он называется определенным интегралом от a до b, от функции f(x) на dx.
. Если существует предел интегральных сумм, при max Dxi ®0, которые не зависят от способа разбиения отрезка [a,b] на части и способа выбора точек Ci, то он называется определенным интегралом от a до b, от функции f(x) на dx.  . Где a – нижний предел, b – верхний предел, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение.
. Где a – нижний предел, b – верхний предел, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение. .
. =
=  .
.
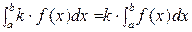

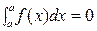

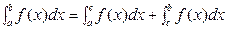
 на [a;b], то
на [a;b], то 
 , где
, где
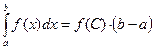
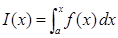 . Геометрически это означает, что соответствующая площадь криволинейной трапеции будет переменной величиной.
. Геометрически это означает, что соответствующая площадь криволинейной трапеции будет переменной величиной. =f(x).
=f(x). . Дадим x приращение Dx и вычислим значение функции. I(x+Dx)=
. Дадим x приращение Dx и вычислим значение функции. I(x+Dx)= 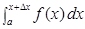 = =
= = 

 =
= 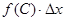 . Рассмотрим предел
. Рассмотрим предел  ,
, т.к. при
т.к. при 
 .
. где F(x)-одна из первообразных f(x).
где F(x)-одна из первообразных f(x). , он является одной из первообразных f(x), т.е.
, он является одной из первообразных f(x), т.е. 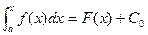 , где C0 – конкретное значение const. Найдем C0. Подставим вместо верхнего предела x=a Þ
, где C0 – конкретное значение const. Найдем C0. Подставим вместо верхнего предела x=a Þ  Þ C0=-F(a) Þ
Þ C0=-F(a) Þ  . Подставим вместо верхнего предела x=b Þ
. Подставим вместо верхнего предела x=b Þ 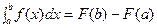
 =
=  =
=  =
= 
 =
=  =
= 
 =
= =
= 

 =
=  =
=  =-1
=-1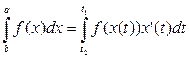 , где
, где  ,
,  .
. =
= 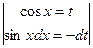 =
= 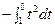 =
=  =
= 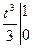 =
= 
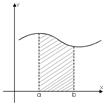 1.16Вычисление площади плоских фигур в декартовой системе координат.
1.16Вычисление площади плоских фигур в декартовой системе координат. Как известно, площадь такой криволинейной трапеции выражается через определенный интеграл: S =
Как известно, площадь такой криволинейной трапеции выражается через определенный интеграл: S =  =
= 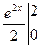 =
=  .
. Замечание: Иногда криволинейную трапецию приходится разбивать на несколько частей. Площадь всей трапеции есть сумма площадей всех частей.
Замечание: Иногда криволинейную трапецию приходится разбивать на несколько частей. Площадь всей трапеции есть сумма площадей всех частей. =
= 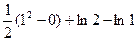 =
=  .
. В общем случае площадь фигуры, ограниченной слева прямой x=a, справа прямой x=b, сверху кривой y=f2(x),снизу кривой y=f1(x), причем f2(x) ³ f1(x).
В общем случае площадь фигуры, ограниченной слева прямой x=a, справа прямой x=b, сверху кривой y=f2(x),снизу кривой y=f1(x), причем f2(x) ³ f1(x).
 . Как известно, площадь криволинейной трапеции равна S=
. Как известно, площадь криволинейной трапеции равна S=  =S, так как dx=x¢(t)×dt, f(x)=y(t). Причем нижний предел интегрирования t1 соответствует точке x=a; x(t1)=a, верхний предел интегрирования t2 соответствует точке x=b; x(t2)=b.
=S, так как dx=x¢(t)×dt, f(x)=y(t). Причем нижний предел интегрирования t1 соответствует точке x=a; x(t1)=a, верхний предел интегрирования t2 соответствует точке x=b; x(t2)=b.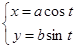
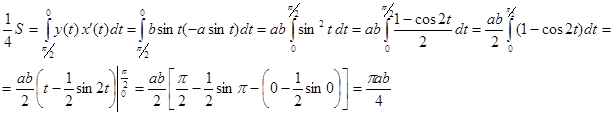
 =pab/4 Þ S= pab (ед2).
=pab/4 Þ S= pab (ед2).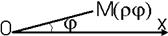 Рассмотрим на плоскости точку О, которую называют полюсом, и луч, выходящий из этой точки, который называется полярной осью. Зададим на полярной оси масштаб. Каждой точке M поставим в соответствие два числа r - длина радиус-вектора |`OM| и j - угол между радиус-вектором точки M и положительным направлением полярной оси.
Рассмотрим на плоскости точку О, которую называют полюсом, и луч, выходящий из этой точки, который называется полярной осью. Зададим на полярной оси масштаб. Каждой точке M поставим в соответствие два числа r - длина радиус-вектора |`OM| и j - угол между радиус-вектором точки M и положительным направлением полярной оси. к полярной оси .
к полярной оси .



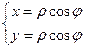 , и от декартовых к полярным:
, и от декартовых к полярным:  ,
, 

 . Заменим площадь i- части площадью кругового сектора
. Заменим площадь i- части площадью кругового сектора  = =
= =  =
=  =
= 
 .
. В ПСК S=
В ПСК S=  .
.
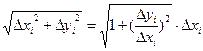
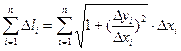 сумма длин звеньев ломанной приближенно равна длине кривой. Переходя к пределу:
сумма длин звеньев ломанной приближенно равна длине кривой. Переходя к пределу: 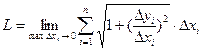 =
=  =
= 
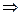

 , где
, где 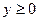 , x=0, x=1.
, x=0, x=1. 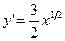

 = =
= = 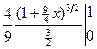 =
= 

 . Рассмотрим подынтегральное выражение
. Рассмотрим подынтегральное выражение 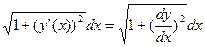 внесем dx под корень
внесем dx под корень  - это выражение называется дифференциалом дуги.
- это выражение называется дифференциалом дуги.  .
.
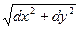 =
=  =
= 

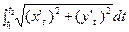 .
. Пример: Найти длину 1 арки циклоиды.
Пример: Найти длину 1 арки циклоиды.

 =
=  =
= 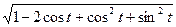 =
= 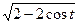 =
=  =
= 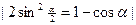 =
=  ==
== 
 =
=  =
= 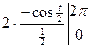 =
= 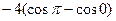 =-4(-1-1)=
=-4(-1-1)=

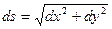 =
=  =
= =
=
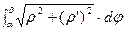
 . В силу симметричности кривой вычислим ½ длины. Полярный угол
. В силу симметричности кривой вычислим ½ длины. Полярный угол  ½L=
½L= 
 =
=  =
= =
=  =
=  =
=  =
= =
= 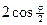
 =
=  =4(1-0)=4 Þ L=4*2=8 (ед).
=4(1-0)=4 Þ L=4*2=8 (ед). ; Причем равенство будет тем точнее, чем больше частей разбиения тела и чем меньше длина отрезка Dxi . Переходя к пределу получаем VT=
; Причем равенство будет тем точнее, чем больше частей разбиения тела и чем меньше длина отрезка Dxi . Переходя к пределу получаем VT= 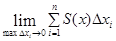 . Этот предел интегральных сумм является определенным интегралом
. Этот предел интегральных сумм является определенным интегралом  где S(x) – площадь поперечного сечения.
где S(x) – площадь поперечного сечения.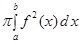 . Если криволинейная трапеция ограниченная линиями
. Если криволинейная трапеция ограниченная линиями  вращается вокруг оси OY, то объем полученного тела вращения VOY=
вращается вокруг оси OY, то объем полученного тела вращения VOY= 

