
|
|
Основные схемы логически правильных рассуждений.Исчисление высказываний. Исчисление высказываний. Основные понятия и определения. Классическое определение исчисления высказываний. 1. Алфавит: и → - связки (логический базис Фреге) (,) - служебные символы. a, b, ..., a1, b1,... - пропозициональные переменные.
2. Формулы: 1)переменные суть формулы. 2)если А,В - формулы, то (А) и (А→В) - формулы.
3. Аксиомы: А1:(A→B(B→A)) A2:((A→B→C))→((A→B)→(A→C)) A3:((B→A)→((B→A)→B).
4. Правило: (A, A→B)/B - Modus ponens Здесь А и В - любые формулы. Таким образом, множество формул бесконечно, хотя задано трёмя схемами аксиом. Множество правил вывода бесконечно, хотя оно задано только одной схемой. Другие связки вводятся определениями A&B:= (A→B);A٧B:= A→B. Простейшим разделом математической логики является исчисление высказываний. Элементарные высказывания рассматриваются в ней как нерасчленяемые "атомы", а составные высказывания - как молекулы, образованные из "атомов" применением логических операций. Пусть X, Y и Z - переменные, вместо которых можно подставлять любые элементарные высказывания (или их значения истинности). Такие переменные могут быть названы высказывательными (или булевыми). С помощью высказывательных переменных и символов логических операций любое высказывание можно формализовать, т.е. заменить формулой, выражающей его логическую структуру. Например, "Если число делится на 2 и на 5, то оно делится на 10 (X Ù У) Þ 2”. Понятие ПФ вводится индуктивно: 1. Символы логических констант 0, 1 являются ПФ. 2. Каждая логическая переменная является ПФ. 3. Если А и В суть ПФ то 4. Никаких других ПФ в логике высказываний нет. Определение закончено. В нем 1 и 2 являются базисными пунктами, где указываются объекты множества, 3 - индуктивный пункт, где даны правила получения из базисных объектов новых объектов, которые будут именоваться этим же термином, 4 - косвенный пункт, где указано, что заданный список исчерпывается. Процедура формализации высказывания состоит из этапов: 1. Если высказывание простое, то ему ставится в соответствие элементарная формула. 2. Если высказывание составное, то нужно: а) выделить все элементарные высказывания и логические связки, образующие составное высказывание; б) заменить их соответствующими символами; в) расставить скобки в соответствии с символами. Элементами логических рассуждений являются утверждения, которые либо истинны, либо ложны, но не то и другое вместе. Такие утверждения называются (простыми) высказываниями. Простые высказывания считаются пропозициональными переменными, принимающими истинностные значения «И» и «Л». Из простых высказываний с помощью логических связок могут быть построены составные высказывания. Обычно рассматривают следующие логические связки:
Название Прочтение Обозначение Отрицание не Ø Конъюнкция и & Дизъюнкция или Ú Импликация если ... то ®
Формулы. Правильно построенные составные высказывания называются (пропозициональными) формулами. Формулы имеют следующий синтаксис: <формула>::=И | Л | <пропозициональная переменная>| (Ø<формула>) | (<формула> & <формула>) | (<формула> Ú <формула>) | (<формула> ® <формула>)
Для упрощения записи вводится старшинство связок (Ø,&, Ú, ®) и лишние связки не допускаются.
Интерпретация Пусть A(x1, ..., xn) - пропозициональная формула, где x1, ..., xn - входящие в нее пропозициональные переменные. Конкретный набор истинности значений, приписанных переменным x1, ..., xn, называется интерпретацией формулы А. Формула может быть истинной (иметь значение И) при одной интерпретации и ложной (иметь значение Л) при другой интерпретации. Значение формулы А в интерпретации I будем обозначать I(A). Формула, истинная при некоторой интерпретации, называется выполнимой. Формула, истинная при всех возможных интерпретациях, называется общезначимой (или тавтологией). Формула, ложная при всех возможных интерпретациях, называется невыполнимой (или противоречием). Пример. AÚØA – тавтология. A&ØA – противоречие, A® ØA – выполнимая формула, она истинна при I(A)=Л.
Логическое следование. Принцип дедукции. Говорят, что формула В логически следует из формулы А, если формула В имеет значение И при всех интерпретациях, при которых формула А имеет значение И. Говорят, что формулы А и В логически эквивалентны (обозначается А↔B или просто А=В), если они являются логическим следствием друг друга. Логически эквивалентные формулы имеют одинаковые значения истинности при любой интерпретации. Наиболее краткий и простой способ вывода основан на теореме дедукции. Далее вставка 5А. Основные схемы логически правильных рассуждений. Наряду с алфавитом и правилами построения сложных высказываний - логических формул, языки логики высказываний содержат правила преобразования логических формул. В алгебре логики -это эквивалентные соотношения, а также правило подстановки и правило замены; в исчислении высказываний - это общие логические аксиомы и правила подстановки и заключения, называемые правилами вывода. Правила преобразования реализуют общие логические законы и обеспечивают логически правильные рассуждения. Корректность допустимых в логике преобразований является фундаментальным свойством формальной (математической) логики. Если описание системы (процесса, явления и т.п.) представлено совокупностью сложных высказываний - логических формул, истинных для данной системы (в данной интерпретации ее простых высказываний), то с помощью допустимых преобразований имеющихся логических представлений о системе может быть выполнен их анализ (синтез), могут быть получены новые представления, характеризующие указанную систему (истинные для данной системы) и т.п. Таким образом, с помощью допустимых в логике преобразований появляется возможность получения новых знанийиз сведений, уже имеющихся. Далее вставка 5В Процесс получения новых знаний, выраженных высказываниями, из других знаний, также выраженных высказываниями, называется рассуждением (умозаключением). Исходные высказывания называются посылками (гипотезами, условиями), а получаемые высказывания – заключением (следствием). Приведем примеры наиболее употребляемых схем логически правильных рассуждений: 1. Правило заключения - утверждающий модус (Modus Ponens): "Если из высказывания А следует высказывание В и справедливо (истинно) высказывание А, то справедливо В" ( Способ спуска). Обозначается:
2. Правило отрицания - отрицательный модус (Modus Tollens): "Еслииз А следует В, но высказывание В неверно, то неверно А” (Доказательство от противного). Обозначается:
3. Правила утверждения-отрицания (Modus Ponendo-Tollens): "Если справедливо или высказывание А, или высказывание В (в разделительном смысле) и истинно одно из них, то другое ложно" (разделительный силлогизм). Обозначается:
4. Правила отрицания-утверждения (Modus Tollen-Ponens): а) "Если истинно или А или В (в разделительном смысле) и неверно одно из них, то истинно другое":
б) "Если истинно А или В (в неразделительномсмысле) и неверно одно из них, то истинно другое" (Дизъюнктивный силлогизм). Обозначается:
5. Правило транзитивности (упрощенное правило силлогизма): "Если из А следует В, а из В следует С, то из А следует С" (гипотетический силлогизм). Обозначается:
6. Закон противоречия: "Если из А следует В и В, то неверно А":
7. Правило контрапозиции: "Если из А следует В, то из того, что неверно В, следует, что неверно А":
8. Правило сложной контрапозиции: "Если из А и В следует С, то из А и С следует В":
9. Правило сечения: "Если из А следует В, а из В и С следует D, то из А и С следует D":
Приведем без пояснений еще несколько правил умозаключений. 10. Правило импортации (объединения посылок):
11. Правило экспортации (разъединения посылок):
12. Правила дилемм: а) б) в) г) Примечание. Для построения логических формул, отражающих указанные выше логически правильные рассуждения, следует все посылки соединить связкой "И" (&) и полученную таким образом обобщенную посылку - связкой "если ..., то ..." (→).Например, правило заключения (Modus Ponens) должно быть представлено логической формулой:
Примерами рассуждений, не являющихся правильными, могут служить: а) б) в) Для того чтобы проверить, является ли данное умозаключение логически правильным, следует восстановить схему рассуждения и определить, относится ли она к схемам логически правильных рассуждений. Однако такая проверка осложняется тем, что схем логически правильных рассуждений бесконечное множество. Для проверки правильности рассуждений может быть использован метод доказательства от противного (закон противоречия – правило 6).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , А Ù В, А Ú В, А Þ В, А Û В также ПФ.
, А Ù В, А Ú В, А Þ В, А Û В также ПФ.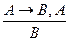 .
.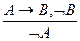 .
.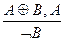 ;
;  .
. ;
;  .
. ;
;  .
.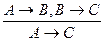 .
. .
. .
.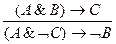 .
. .
. .
. .
. (простая конструктивная дилемма);
(простая конструктивная дилемма); (сложная конструктивная дилемма);
(сложная конструктивная дилемма); (простая деструктивная дилемма);
(простая деструктивная дилемма); (сложная деструктивная дилемма).
(сложная деструктивная дилемма). .
.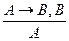

 и др.
и др.