
|
|
Разложение многочлена с действительными коэффициентами на линейные и квадратные множителиИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ План 1. Многочлен в комплексной плоскости. Теорема Безу. Корни многочлена. 2. Разложение многочлена с действительными коэффициентами на линейные и квадратные множители. 3. Интегрирование рациональных функций путем разложения на простейшие дроби.
Многочлен в комплексной плоскости. Теорема Безу. Корни многочлена Перед тем как непосредственно перейти к вопросу об интегрировании рациональных функций необходимо рассмотреть алгебру многочленов, основные свойства и правила преобразований рациональных функций, что и делается в дальнейшем. Опр. Многочленом (полиномом)
где коэффициенты Опр. Число
называется корнем многочлена (1). ТЕОРЕМА (основная теорема алгебры). Всякий многочлен степени ( ТЕОРЕМА БЕЗУ. Число
Опр. Если многочлен Если
где ТЕОРЕМА. Если
где Если же среди корней многочлена имеются кратные, то данный многочлен
где Таким образом, если учитывать кратность каждого корня, то всякий многочлен степени ТЕОРЕМА. Если комплексное число Используя это свойство, заменим в разложении многочлена на множители комплексные выражения
Здесь Тогда разложение (5) многочлена
где Разложение (6) многочлена на множители единственно, поскольку оно однозначно определяется корнями этого многочлена и их кратностями.
Разложение многочлена с действительными коэффициентами на линейные и квадратные множители Опр. Пусть Если рациональная дробь
где ТЕОРЕМА. Пусть
здесь
такие, что
Опр. Рациональные дроби вида
где Таким образом, всякая правильная рациональная дробь может быть разложена в сумму элементарных рациональных дробей. Различают четыре типа элементарных рациональных дробей. 1-й тип. Рациональные дроби вида 2-й тип. Рациональные дроби вида, 3-й тип. Рациональные дроби вида, 4-й тип. Рациональные дроби вида, На практике приведение рациональной дроби к выражению (8) осуществляется с помощью метода неопределенных коэффициентов, который состоит из следующих шагов. 1. Выполняется разложение знаменателя 2. Для данной дроби 3. Обе части равенства приводятся к общему знаменателю, который далее отбрасывается. 4. Приравниваются коэффициенты у полученных многочленов, что приводит к системе 5. В результате решения полученной системы находятся искомые коэффициенты Поиск коэффициентов Пример. Выполним разложение на элементарные дроби выражения
Представим искомое разложение в виде
и, приводя к общему знаменателю, получим
Отбросим знаменатель
раскроем скобки возле каждого искомого коэффициента
и сгруппируем выражения в правой части по степеням
Приравняем коэффициенты при одинаковых степенях
и запишем полученную систему уравнений
Решением этой системы являются значения искомых коэффициентов
Другим способом поиска неизвестных
вещественных корней знаменателя – подставляя – подстановка – подстановка Таким образом, искомое разложение имеет вид

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 -й степени называется выражение вида
-й степени называется выражение вида , (1)
, (1)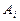 ,
,  , – постоянные числа (как правило, действительные), и
, – постоянные числа (как правило, действительные), и 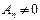 . Число
. Число  (вообще говоря, комплексное), такое, что
(вообще говоря, комплексное), такое, что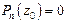 ,
, ) имеет по крайней мере один корень, действительный или комплексный.
) имеет по крайней мере один корень, действительный или комплексный. тогда и только тогда, когда многочлен
тогда и только тогда, когда многочлен  делится без остатка на
делится без остатка на  :
: . (2)
. (2) делится на
делится на  (
(  – неотрицательное целое) и не делится на
– неотрицательное целое) и не делится на  , то число
, то число  , то выполняется равенство
, то выполняется равенство . (3)
. (3) – такой многочлен степени
– такой многочлен степени  , что
, что  .
. ,
,  ,…,
,…,  – корни многочлена
– корни многочлена  , (4)
, (4) – коэффициент при
– коэффициент при  .
. , (5)
, (5) – различные корни многочлена
– различные корни многочлена  (
(  ) – соответствующие кратности корней
) – соответствующие кратности корней  .
. является корнем многочлена (1) с вещественными коэффициентами, то сопряженное число
является корнем многочлена (1) с вещественными коэффициентами, то сопряженное число 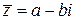 также является его корнем и притом той же кратности, что и
также является его корнем и притом той же кратности, что и  .
. и
и 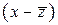 их произведением
их произведением  , которое является многочленом второй степени с действительными коэффициентами:
, которое является многочленом второй степени с действительными коэффициентами: .
.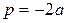 ,
, 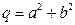 ,
,  .
. , (6)
, (6) ,
,  ,
, 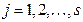 и все коэффициенты
и все коэффициенты  , …,
, …,  ;
;  ,
, 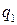 , …,
, …, 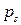 ,
,  вещественны. При этом
вещественны. При этом  – все вещественные корни многочлена
– все вещественные корни многочлена  соответствует множитель вида
соответствует множитель вида  .
. и
и  – многочлены с вещественными коэффициентами. Рациональная дробь
– многочлены с вещественными коэффициентами. Рациональная дробь  – называется правильной, если степень многочлена
– называется правильной, если степень многочлена  ,
, ,
, 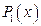 и
и  – некоторые многочлены, а
– некоторые многочлены, а  – правильная рациональная дробь.
– правильная рациональная дробь. и
и  , (7)
, (7)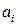 – попарно различные вещественные корни многочлена
– попарно различные вещественные корни многочлена 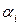 ,
,  , а выражения
, а выражения 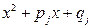 соответствуют попарно различным комплексным корням
соответствуют попарно различным комплексным корням  и
и 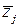 кратности
кратности  ,
,  . Тогда существуют вещественные числа
. Тогда существуют вещественные числа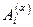 ,
, 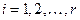 ,
,  ,
, и
и  ,
,  ,
, 

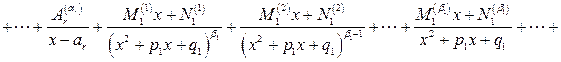
 . (8)
. (8) ,
,  ,
, ,
,  ,
, 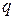 ,
,  ,
, 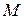 и
и  – действительные числа, а
– действительные числа, а 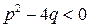 , называются элементарными рациональными дробями.
, называются элементарными рациональными дробями.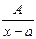 ;
; ,
,  ;
; ;
; ,
,  .
.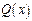 данной дроби
данной дроби 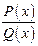 на множители.
на множители.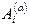 ,
,  ,
,  которого считаются неизвестными (
которого считаются неизвестными (  ,
,  ).
). ,
,  ,
,  .
. . В этом случае число неизвестных коэффициентов и соответствующих уравнений может быть уменьшено. В некоторых случаях можно вообще обойтись без решения системы.
. В этом случае число неизвестных коэффициентов и соответствующих уравнений может быть уменьшено. В некоторых случаях можно вообще обойтись без решения системы. .
.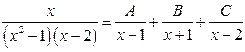
 .
. ,
,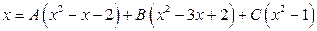
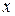 :
: .
. :
:

 :
:

 :
:
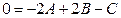
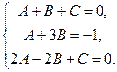
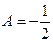 ,
,  ,
, 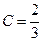 .
. ,
,  и
и  является подстановка в выражение
является подстановка в выражение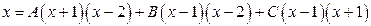
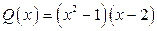 :
: , получим
, получим  , откуда следует
, откуда следует  ;
; дает равенство
дает равенство  , откуда
, откуда  ;
; приводит к уравнению
приводит к уравнению 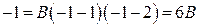 , решением которого является
, решением которого является  .
. .
.