
|
|
Вычисление площадей плоских фигурОпределенный интеграл. Пусть функция
Разобьем отрезок [a,b] на n произвольных частей точками
Длину каждого i-го отрезка разбиения назовем
Внутри каждого отрезка разбиения выберем произвольно по точке
Составим сумму
Выражение вида (1) называется интегральной суммой функции f(x) по отрезку [a,b]. Если функция Опр. Предел интегральной суммы функции f(x) по отрезку [a,b] при стремлении длины наибольшего из частичных отрезков к нулю, называется определенным интегралом от функции f(x) по отрезку [a,b] и обозначается
Числа а и в называют нижним и верхним пределами интегрирования. Функция называется интегрируемой на отрезке [a,b]. Любая непрерывная на отрезке функция интегрируема на этом отрезке. Геометрический смысл определенного интеграла.
Из рисунка видно, что интегральная сумма равна площади ступенчатой фигуры, образованной из прямоугольников шириной
Свойства определенного интеграла. 1. 2. 3. 4. 5. Пусть функция y=f(x) интегрируема на отрезках [a,c] [b,c], a<c<b. Тогда она интегрируема и на отрезке [a,b] , причем
6. Если функции f(x) и g(x) интегрируемы по отрезку [a,b], то и их сумма также интегрируема по отрезку [a,b], причем
7. Если на отрезке [a,b] выполняется неравенство
8. Если промежуток интегрирования симметричен, то
и
§2. Интеграл с переменным верхним пределом. Вычисление определенного интеграла.
Пусть функция y=f(x) определена и непрерывна на отрезке [a,b]. Тогда она интегрируема как на отрезке [a,b], так и на любом меньшем отрезке [а,х], где
является функцией от х. Она называется интегралом с переменным верхним пределом и является первообразной для функции f(x). Другими словами, функция Ф(х) в каждой своей точке имеет производную, равную f(x):
Теперь перейдем к вопросу вычисления определенного интеграла. Теорема. Пусть функция y=f(x) определена и непрерывна на отрезке [a,b] и F(х) является первообразной для функции f(x). Тогда
(Эта основная формула интегрального исчисления называется формулой Ньютона-Лейбница. Она позволяет сводить вычисление определенного интеграла к нахождению первообразной.) Док-во. Пусть функция y=f(x) имеет некоторую первообразную F(x). Тогда F(x)=Ф(x)+C, где
Пример.
Замена переменной в определенном интеграле.
Теорема. Пусть функция y=f(x) непрерывна на отрезке [a,b], а функция x=φ(t) определена на отрезке [α,β] и имеет непрерывную производную внутри этого отрезка, причем φ(α)=a, φ(β)=b и φ([α,β])=[a,b]. Тогда
Док-во. Пусть F(x) – первообразная для функции f(x), тогда
Пример. Найти
Применим подстановку
Интегрирование по частям в определенном интеграле. Если функции
Пример. Найти
Решение. Воспользуемся формулой интегрирования по частям. Полагая Следовательно:
Приложения определенного интеграла. Вычисление площадей плоских фигур
1. Для непрерывной неотрицательной на отрезке [а,в] функции y=f(x) площадь фигуры, ограниченной графиком этой функции, осью Ох и прямыми х=а и х=в вычисляется по формуле:
2.Для непрерывной неположительнойна отрезке [а,в] функции y=f(x) площадь фигуры, ограниченной графиком этой функции, осью Ох и прямыми х=а и х=в вычисляется по формуле:
3. Пусть
Отметим, что данная формула выполняется и в случае, когда функции f и g отрицательны.
4. Площадь криволинейной трапеции, прилегающей к оси
Пример. Найти площадь фигуры, ограниченной линиями
2-х2=х х2+х-2=0 х=1 и х=-2. Таким образом,
=

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 определена и непрерывна (а значит, ограничена) на [a,b].
определена и непрерывна (а значит, ограничена) на [a,b].

 .
. ,
,  .
.
 .
.
 . (1)
. (1) непрерывна на отрезке
непрерывна на отрезке  , то существует предел интегральной суммы при условии, что длина наибольшего из частичных отрезков стремится к нулю, и он не зависит от способа разбиения отрезка
, то существует предел интегральной суммы при условии, что длина наибольшего из частичных отрезков стремится к нулю, и он не зависит от способа разбиения отрезка  .
.
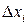 , высотой
, высотой 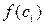 . При неограниченном измельчении длин отрезков разбиения площадь этой фигуры стремится к площади криволинейной трапеции. Следовательно, определенный интеграл в геометрическом смысле равен площади криволинейной трапеции, заключенной между графиком неотрицательной функции и осью Ох на отрезке [a,b].
. При неограниченном измельчении длин отрезков разбиения площадь этой фигуры стремится к площади криволинейной трапеции. Следовательно, определенный интеграл в геометрическом смысле равен площади криволинейной трапеции, заключенной между графиком неотрицательной функции и осью Ох на отрезке [a,b]. ;
; ;
; ;
; ;
; ;
; .
. , то
, то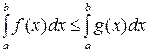 .
. , если
, если  , если
, если  - четная функция.
- четная функция. [a,b]. Значит, величина
[a,b]. Значит, величина
 .
. .
.

 .▲
.▲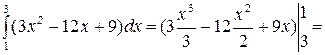

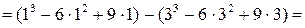 1-6+9-27+54-27=4.
1-6+9-27+54-27=4. .
. и
и 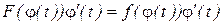 . Тогда
. Тогда

 .▲
.▲ .
. . Найдем новые пределы интегрирования: при
. Найдем новые пределы интегрирования: при  ; при
; при  .
. .
. и
и  непрерывны вместе со своими производными на отрезке
непрерывны вместе со своими производными на отрезке  , то имеет место следующая формула интегрирования по частям:
, то имеет место следующая формула интегрирования по частям: .
.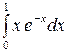 .
. ,
, 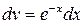 , имеем:
, имеем: 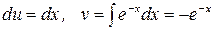 .
. .
.
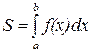 .
.
 .
.
 на отрезке [а,в]. Тогда площадь фигуры, ограниченной сверху графиком f(x), снизу графиком g(x) и прямыми х=а и х=в вычисляется по формуле:
на отрезке [а,в]. Тогда площадь фигуры, ограниченной сверху графиком f(x), снизу графиком g(x) и прямыми х=а и х=в вычисляется по формуле: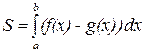 .
.
 , вычисляется по формуле
, вычисляется по формуле .
.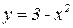 и у=х.
и у=х. Решение. Найдем точки пересечения двух данных линий.
Решение. Найдем точки пересечения двух данных линий. =
= (кв.ед.)
(кв.ед.)