
|
|
Импульсно-кодовая модуляцияИсследование методов кодирования в тракте передачи данных Теоретическая часть OSI (Open System Interconnections) reference model – эталонная модель взаимодействия открытых систем. Эта модель была разработана международной организацией по стандартизации в 1984г., и она позволяет универсальным образом описать логику информационного обмена между взаимосвязанными системами и абонентами. Эталонная модель содержит семь уровней. На самом нижнем (физическом) уровне этой модели между терминалом и сетевым оборудованием обеспечивается связь, а на самом верхнем (прикладном) – обслуживание средств пользователей. Уровни 1-3 называются нижними, а уровни 5-7 верхними. Уровень 4 является транспортной средой между нижними и верхними уровнями. Два нижних уровня модели могут реализоваться как аппаратно, так и программно, а верхние - преимущественно программно. Основная идея модели состоит в том, что одни и те же уровни разных систем взаимодействуют по идентичным протоколам и предоставляют сервис для вышестоящих уровней. При переходе от одного уровня к другому к полезной информации добавляются заголовки, содержащие служебные данные, необходимые другим уровням. Для реализации системы связи не обязательно использовать все семь уровней модели OSI. Так, обмен данными в радиосетях может быть описан с помощью трех нижних уровней, что резко уменьшает число межуровневых связей, а, следовательно, упрощает модель.
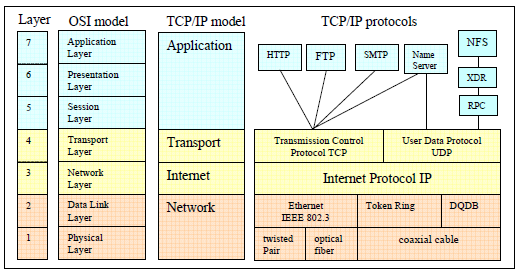
На Рис. 1 сравнивается модель OSI с моделью TCP/IP и их протоколами. Исторически так сложилось, что развитию цифровых сетей передачи данных предшествовало развитие телефонных сетей. Инженерами внедрялись различные технологи для повышения качества передачи человеческой речи по телефонным каналам связи. Однако аналоговая передача сигналов приводила к существенной проблеме – накопление искажений и шумов в процессе ретрансляции этих сигналов. Для устранения этой проблемы Алек Ривс в 1937 году впервые применил импульсно-кодовую модуляцию (ИКМ) для голосового сигнала с частотой дискретизации 8кГц при 8-битовом аналого-цифровом преобразовании (АЦП). Но в то время еще не существовало эффективных технологических средств для реализации такой схемы. Цифровая связь берет свое начало в 70-х годах 20 века. Именно в это время начинается бурное развитие цифровой электроники и появляется возможность реализации схемы Алека Ривса. В основе аналого-цифрового преобразования лежит теорема Найквиста-Котельникова, в которой требуется, чтобы частота дискретизации сигнала всегда превосходила полосу обрабатываемого сигнала более чем в два раза. Для передачи голоса в аналоговой телефонии выбран частотный диапазон от 300 до 3400 Гц. В соответствие с теоремой Найквиста-Котельникова[1] для качественной передачи голоса в телефонных сетях достаточно выбрать частоту дискретизации Как правило, аналого-цифровое преобразование осуществляется на прикладном уровне модели OSI. Импульсно-кодовая модуляция
Концептуально преобразование аналогового сигнала непрерывного во времени в цифровой, имеющий дискретную структуру во временной области, очень простая задача, состоящая из двух процессов: дискретизации и квантования. Дискретизатор конвертирует непрерывный сигнал  в дискретный сигнал в дискретный сигнал 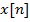 , путем измерения амплитуды непрерывного сигнала через строго соблюдаемые интервалы времени , путем измерения амплитуды непрерывного сигнала через строго соблюдаемые интервалы времени  . Квантователь конвертирует амплитуду непрерывного сигнала . Квантователь конвертирует амплитуду непрерывного сигнала  в дискретную амплитуду в дискретную амплитуду 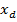 . Структурная схема ИКМ представлена на Рис. 2. . Структурная схема ИКМ представлена на Рис. 2.К сожалению, результирующий цифровой сигнал немного отличается от дискретного сигнала на величину, называемой ошибкой квантования или цифровым шумом (Рис. 3), который равен:
Ошибка квантования появляется в процессе кодирования, поскольку амплитуда исходного сигнала может быть представлена исключительно
Выходной сигнал отображен на вертикальной оси  для дискретного значения для дискретного значения 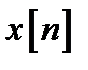 амплитуды аналогового сигнала. Важно заметить, что значения амплитуды аналогового сигнала, незначительно отличающиеся друг от друга, в процессе квантования бут закодированы одним двоичным числом, в результате чего эти амплитуды после обратного преобразования будут иметь одинаковые значения (Рис. 3,а.). амплитуды аналогового сигнала. Важно заметить, что значения амплитуды аналогового сигнала, незначительно отличающиеся друг от друга, в процессе квантования бут закодированы одним двоичным числом, в результате чего эти амплитуды после обратного преобразования будут иметь одинаковые значения (Рис. 3,а.).
Из вышеизложенного на интуитивном уровне понятно, что существуют две проблемы в процессе преобразования аналогового сигнала в цифровой сигнал. Первой проблемой является максимальный поддерживаемый АЦП диапазон сигнала или, другими словами, размах аналогового сигнала должен точно укладываться в диапазон уровней квантования. Если же сигнал выходит за этот диапазон он будет усечен или искажен. Второй неизбежной проблемой является конечное число уровней квантования, приводящее к уменьшению репрезентативной точности и в итоге к появлению шума квантования (Рис. 4). Рассматривая процесс квантования через призму статистического аппарата можно увидеть следующее: 1. Процесс квантования приводит к дискретности функции плотности распределения вероятности квантованного сигнала. 2.
Функция плотности распределения вероятности ошибки квантования (Рис. 5) укладывается в диапазон:  , где , где  – шаг квантования. – шаг квантования.
Из пункта 2 становится понятно, что чем меньше шаг квантования, тем выше репрезентативная точность и тем меньше мощность шума. Однако возникает насущный вопрос, - каким параметром количественно можно описать мощность шума, и как он связан с количеством бит, характеризующих диапазон квантования? В нашем случае абсолютно не важно, является ли ошибка квантования, полученная по формуле, положительной или отрицательной, гораздо важнее – величина этой ошибки! Более того, наибольший интерес вызывает мощность этой ошибки, оказывающая влияние на сигнал, которую можно выразить следующей формулой:
где N – количество элементов. Если учитывать, что входной сигнал, имеющий пиковую амплитуду
Как показано на Рис. 5 среднее значение шума квантования равно нулю, и любое отдельное значение равномерно укладывается в интервал от
Из теории вероятности также известно, что площадь под кривой функции плотности распределения вероятности равна единице. Ширина диапазона ошибки квантования равна
Результат, полученный в выражении характеризует мощность шума квантования в зависимости от ширины шага квантования. Однако больший интерес вызывает зависимость мощности шума квантования от диапазона квантования, т.е. от разрядности АЦП. Используя формулу перезапишем выражение :
В соответствие с этим получаем:
Выразим отношение мощности сигнала к мощности шума в децибелах:
Как видно из выражения SNR зависит от соотношения
Физический смысл выражения весьма прост: с добавлением (уменьшением) одного бита в АЦП увеличивается (уменьшается) шум квантования на 6 дБ. Поэтому, для того чтобы осуществить преобразование непрерывного сигнала в цифровой сигнал с минимальными искажениями, необходимо увеличить точность шага квантования Полученный, в результате преобразования, цифровой поток формируется в блоки данных и передается на следующий уровень модели OSI, где каждый блок данных обрамляется соответствующим заголовком, обеспечивающим уникальность этих данных во всем информационном потоке. Процесс добавления служебных данных на каждом уровне называется инкапсуляцией. Этот процесс осуществляется вплоть до физического уровня модели OSI, на котором, поток «непрерывных» битов информации, кодируется в электрические или оптические импульсы, в зависимости от физической среды передачи данных. Физический уровень Когда речь заходит о технологии Ethernet то предполагается, что говорится о первом и втором уровне модели OSI. Физический уровень состоит из среды передачи (оптический кабель или витая пара) и методов кодирования информации для каждой скорости передачи. На Рис. 6 представлена структура канального и физического уровня Ethernet 100Base-T в соответствии со стандартом IEEE802.3. Здесь MDI – «Medium Dependent Interface» - интерфейс, зависящий от среды передачи данных; PMA – «Physical Medium Attachment» - дополнение физической среды передачи; PCS – «Physical Coding Sublayer» - подуровень физического кодирования; MII – «Media Independent Interface» - интерфейс между подуровнями, не зависящий от типа линии передачи. MDI на Рис. 6 - это устройство для соединения линии связи с трансивером. Подуровень PMA включает в себя трансивер, а также схему синхронизации принимаемых данных. Подуровень PCS обеспечивает схему кодирования, мультиплексирования и синхронизации потока символов, а также выравнивание спектра кодового сигнала, демультиплексирование и декодирование. Подуровень согласования обеспечивает согласование интерфейса MII с MAC - уровнем. Интерфейс MII, не зависящий от типа среды передачи, обеспечивает связь между уровнем MAC и подуровнем PHY. I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AF9plGDFAAAA2gAAAA8AAABkcnMvZG93bnJldi54bWxEj09LAzEUxO+C3yE8wYu0WasuZdu0FGFB xIu19M/tsXndbLt52W5iG7+9KQgeh5n5DTOdR9uKM/W+cazgcZiBIK6cbrhWsPoqB2MQPiBrbB2T gh/yMJ/d3kyx0O7Cn3RehlokCPsCFZgQukJKXxmy6IeuI07e3vUWQ5J9LXWPlwS3rRxlWS4tNpwW DHb0aqg6Lr+tgrCLeXw4vKzx9PSx2b6bMuZVqdT9XVxMQASK4T/8137TCp7heiXdADn7BQAA//8D AFBLAQItABQABgAIAAAAIQAEqzleAAEAAOYBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9U eXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhAAjDGKTUAAAAkwEAAAsAAAAAAAAAAAAAAAAAMQEAAF9y ZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABIAAAAAAAAAAAAAAAAALgIAAGRy cy9waWN0dXJleG1sLnhtbFBLAQItABQABgAIAAAAIQBfaZRgxQAAANoAAAAPAAAAAAAAAAAAAAAA AJ8CAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABAD3AAAAkQMAAAAA ">
Описанная структура 100Base- T с помощью MII может быть подключена к физическим уровням типа 100Base- T4 (использует 4 неэкранированные витые пары категории не ниже 3), 100Base-TX (использует 2 неэкранированные или экранированные витые пары категории не ниже 5), 100 Base-FX (использует два многомодовых оптических кабеля) и 100Base-T2 (использует две неэкранированные витые пары категории не ниже 3). В структуре на Рис. 6 может еще присутствовать необязательный блок автоматического выбора скорости передачи. Термин «100 Base-X» используется для общего обозначения 100Base-TX и 100 Base-FX. Методы кодирования Такие стандарты как 10Base-T и 100 Base-TX используют манчестерский код для скорости передачи 10 Мбит/с и 4B/5B кодирование в сочетании с NRZI (NRZ Inverted - инвертированный NRZ, см. Рис. 7) для скорости 100 Мбит/с. При низкой скорости обмена (10 Мбит/с) используется манчестерский код, при котором логическая единица кодируется переходом сигнала с низкого уровня на высокий (Рис. 7), а логический ноль - переходом с высокого уровня на низкий. Недостатком манчестерского кода является широкая полоса частотного спектра, связанная с необходимостью переключения уровней сигнала при поступлении каждой двоичной цифры (сравните его с NRZ-кодом на Рис. 7). В спектре манчестерского кода присутствует две ярко выраженные гармоники, которые при скорости передачи 10 Мбит/с составляют 10 МГц при передаче всех единиц и 5 МГц - для сигнала, состоящего из чередующихся нулей и единиц. Для уменьшения помех, излучаемых линией передачи при скорости 100 Мбит/с (100Base-TX), используется NRZI-кодирование, при котором двоичной единице соответствует смена уровня NRZI-сигнала, а нулю - ее отсутствие (Рис. 7). Высокий или низкий уровень NRZI-сигнала устанавливается в зависимости от того, какой уровень был до него. Логической единице соответствует изменение сигнала независимо от того, какой уровень присутствовал на шине ранее. Уровень не изменяется, если нужно закодировать логический ноль. Иначе говоря, логическая единица при NRZI-кодировании инвертирует предыдущее логическое состояние, поэтому в названии
кода присутствует слово «Inverted». NRZI-кодирование, как и NRZ, позволяет передать в два раза больше информации по сравнению с манчестерским кодированием при той же частоте смене уровней сигнала и, соответственно, в два раза понизить максимальную частоту излучаемых помех при той же скорости передачи информации. Максимальная частота смены уровней при NRZI кодировании понижается до 62,5 МГц по сравнению с максимальной частотой смены уровней сигнала 125 МГц для скорости передачи 100 Мбит/с (пояснения см. ниже, при описании 4В/5В кодирования). При переходе к скорости передачи 100 Мбит/с проблема снижения мощности излучаемых помех становится особенно остро, поэтому для дальнейшего снижения ширины спектра сигнала в 100Base-TX вместо двухуровневого сигнала используется трехуровневый MLT-3 («MultiLevel Threshold-3»- «многоуровневый 3-пороговый»), см. Рис. 7. Благодаря тому, что для кодирования информации используются три уровня (а не два), увеличивается количество информации, которое может быть закодировано в сигнале при той же ширине спектра и длительности сигнала. Максимальная частота смены уровней сигнала при скорости передачи 100 Мбит/с снижается с 62,5 МГц при NRZI-кодировании до 31,25 МГц при сочетании NRZI кода с MLT-3. Поскольку при использовании NRZI-кодирования последовательность нулей кодируется нулевым уровнем сигнала, в передаваемом сигнале появляются последовательности из нескольких повторяющихся нулей, которые порождает проблему синхронизации на стороне приемника. Для ее устранения используют кодирование 4B/5B. Суть его состоит в следующем. К каждой тетраде (4 бита) передаваемых данных добавляется 5-й бит. Получившееся слово длиной 5 бит позволяет записать 32 кодовых комбинаций, из которых исключают комбинации, имеющие три и более нулей. Оставшиеся комбинации ставят в соответствие шестнадцатеричным числам от 0 до F, получая, таким образом, таблицу кодирования (Табл. 1). Этот подход позволяет обеспечить, по крайней мере, 2 фронта сигнала на одну тетраду, что упрощает синхронизацию данных в приемнике. Добавление пятого бита (25% от длины тетрады) влечет за собой необходимость увеличения частоты передачи со 100 МГц до 125 МГц для сохранения эффективной пропускной способности канала 100 Мбит/с. Табл. 1 – Кодирование 4B/5B
Диапазон частот, в котором мощность излучаемых помех максимальна, зависит от распределения нулей и единиц в передаваемых данных. При 4B/5B кодировании максимальная мощность помех приходится на частоту, с которой повторяются 5-битные последовательности. Для уменьшения помех можно выбрать такое шифрование (скремблирование) передаваемых данных, при котором мощность помех будет распределена по всему диапазону частот равномерно. Это выполняется с помощью блока скремблирования и позволяет на 20 дБ (в 10 раз) снизить мощность основной гармоники, распределив ее равномерно по всему диапазону излучаемых частот. Основная идея скремблирования заключается в побитном вычислении результирующего кода на основании битов исходного кода и полученных в предыдущих тактах битов результирующего кода. Например, скрэмблер может реализовывать следующее соотношение:
Здесь Например, для исходной последовательности 110110000001 скремблер даст следующий результирующий код (первые три цифры результирующего кода будут совпадать с исходным кодом, так как еще нет нужных предыдущих цифр):
Таким образом, на выходе скрэмблера появится код 110001101111, в котором нет последовательности из шести нулей, присутствовавшей в исходном коде. После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную последовательность на основании обратного соотношения:
Различные алгоритмы скрэмблирования отличаются количеством слагаемых, дающих цифру результирующего кода, и сдвигом между слагаемыми. Перечисленные методы уменьшают ширину спектра до 31,25 МГц при скорости передачи 100 Мбит/с. Структурная схема блока PHY показана на Рис. 8. Блок состоит из приемного (внизу) и передающего (вверху) канала, которые через изолирующие трансформаторы подключаются к линии передачи (две витые пары) через разъем RJ-45. Трансформаторы используется для изоляции трансивера от высоких синфазных напряжений, которые могут появляться на линии вследствие электромагнитных и электростатических наводок.
Как было сказано выше и кодирование 4В/5В и скремблирование необходимы для уменьшения длинных последовательностей нулей и единиц, состоящих в исходной битовой последовательности. Появление же таких последовательностей явление вероятностное, вносящее неопределенность в систему передачи данных. Мерой неопределенности в системе связи является понятие, введение Клодом Шенноном, информационная энтропия. Информационная энтропия В качестве меры неопределенности системы в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии в теории информации является основным. Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:
Здесь
В нашем случае появление четырех единиц или нулей в исходной последовательности приводят к появлению постоянной составляющей на зажимах передатчика. Однако изолирующий трансформатор не обеспечивает прохождения через себя постоянного электрического тока, что может привести к возникновению потерь в линии связи, т.е. к неопределенности. Соответственно, чем больше таких 4-х битовых слов присутствует в исходной последовательности, тем больше величина информационной энтропии и наоборот. Именно по этой причине энтропия рассчитывается для 4-х битовых слов, состоящих только из 0 или 1. Вычисление энтропии сводится к нахождению вероятности появления, интересующего нас 4-х битового слова, в данном случае 0000 или 1111. Поэтому исходная последовательность разбивается на слова, состоящих из 4-х бит, и определяется количество появления каждого слова в исходной битовой последовательности. В нашем случае количество неповторяющихся слов ограничено и равно В результате всех преобразований (Рис. 8), полученная кодовая последовательность кодируется в электрический, электромагнитный или световой сигнал, в зависимости от среды передачи данных. Начиная с этого момента, мы уже имеем дело не с битовой последовательностью, а с последовательностью импульсов, обладающих характеристиками: длительность импульса, амплитуда импульса…. Однако среда передачи данных не является идеальной и вносит свои искажения в передаваемый сигнал, и, следовательно, искажает форму прямоугольного импульса. Причину возникновения искажения сигнала поможет узнать математический анализ Фурье. Ряды Фурье. В начале XIX столетия французский математик Жан-Батист Фурье (Jean-Baptiste Fourier) доказал, что любая периодическая функция Информационный сигнал, имеющий конечную длительность (все информационные сигналы имеют конечную длительность), может быть разложен в ряд Фурье, если представить, что весь сигнал бесконечно повторяется снова и снова (то есть интервал от Т до 2Т полностью повторяет интервал от 0 до Т, и т. д.).
Математически, сигнал, повторяющийся через определенный период Т можно описать следующим выражением  . В связи с тем, что реальные сигналы (функции) имеют период отличный от 2π, то более подходящим в аналитических расчетах является использование угловой частоты . В связи с тем, что реальные сигналы (функции) имеют период отличный от 2π, то более подходящим в аналитических расчетах является использование угловой частоты  , измеряемой в радианах в секунду. Смысл этого выражения проиллюстрирован на рис. 9. , измеряемой в радианах в секунду. Смысл этого выражения проиллюстрирован на рис. 9.
Теорема Фурье утверждает, что любой периодический сигнал
или можно записать выражение , учитывая, что период функции не равен 2π:
Коэффициенты
Пределы интегрирования могут также находиться в диапазоне Из формулы можно увидеть, что функция
Если записать коэффициенты ряда Фурье в виде
где амплитуда гармоники- фазовая составляющая гармоники - то получим эквивалентную форму ряда Фурье:
Амплитудный спектр можно изобразить графически вертикальными отрезками длины An: по оси ординат отмечаем значения частот
Аналогично изображается фазовый спектр. Поскольку периодическая функция представляется бесконечной суммой гармоник с кратными частотами, то ее спектр носит дискретный характер. Для многих практических приложений достаточно знать лишь амплитудный спектр функции. Изучая амплитудный спектр ряда Фурье периодического колебания, легко найти те значения частот, которым соответствуют большие значения An, т.е. те частоты, которым соответствуют гармоники с относительно большой ролью в образовании периодического процесса. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
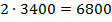 Гц. Однако для оцифровки голосового сигнала была выбрана частота дискретизации 8кГц, обеспечивающая некоторый запас качества. Следующим шагом в цифровом преобразовании голосового сигнала является квантование амплитуды этого сигнала. В соответствие с принятыми стандартами во многих странах выбрано различное количество уровней квантования, в частности в Европейских странах выбран 8-битовый код, что обеспечивает 28=256 уровней квантования, а в США и Японии 7-битовый код.
Гц. Однако для оцифровки голосового сигнала была выбрана частота дискретизации 8кГц, обеспечивающая некоторый запас качества. Следующим шагом в цифровом преобразовании голосового сигнала является квантование амплитуды этого сигнала. В соответствие с принятыми стандартами во многих странах выбрано различное количество уровней квантования, в частности в Европейских странах выбран 8-битовый код, что обеспечивает 28=256 уровней квантования, а в США и Японии 7-битовый код. .
.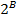 дискретными уровнями, в то время как амплитуда аналогового сигнала представлена бесконечным количеством уровней. На Рис. 3 изображен квантователь с восьмью уровнями квантования
дискретными уровнями, в то время как амплитуда аналогового сигнала представлена бесконечным количеством уровней. На Рис. 3 изображен квантователь с восьмью уровнями квантования  . Входной аналоговый сигнал представлен на горизонтальной, непрерывной во времени, оси
. Входной аналоговый сигнал представлен на горизонтальной, непрерывной во времени, оси 

 , (b) квантованный сигнал
, (b) квантованный сигнал  (3 бита), (c) ошибка квантования e
(3 бита), (c) ошибка квантования e 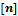 (3 бита), (d) ошибка квантования e
(3 бита), (d) ошибка квантования e  ,
, , полностью перекрывается диапазоном квантования, то шаг квантования будет соответствовать следующему выражению:
, полностью перекрывается диапазоном квантования, то шаг квантования будет соответствовать следующему выражению: ,
,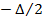 до
до  . Это означает, что функция плотности распределения вероятности шума квантования имеет равномерное распределение с нулевым средним. В соответствие с теорией вероятности любую функцию плотности распределения вероятности можно описать двумя параметрами средним и дисперсией, которые вычисляются по следующим формулам:
. Это означает, что функция плотности распределения вероятности шума квантования имеет равномерное распределение с нулевым средним. В соответствие с теорией вероятности любую функцию плотности распределения вероятности можно описать двумя параметрами средним и дисперсией, которые вычисляются по следующим формулам: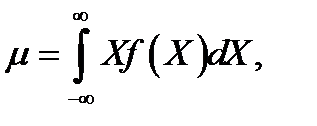
 .
.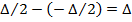 . Соответственно
. Соответственно 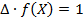 , тогда
, тогда 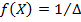 . Отсюда получаем уравнение для дисперсии шума квантования, с учетом того, что среднее значение равно 0:
. Отсюда получаем уравнение для дисперсии шума квантования, с учетом того, что среднее значение равно 0: .
.


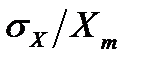 , т.е. от соотношения пиковой амплитуды сигнала к среднеквадратическому отклонению (СКО) значений этого сигнала. Естественно пиковая амплитуда сигнала
, т.е. от соотношения пиковой амплитуды сигнала к среднеквадратическому отклонению (СКО) значений этого сигнала. Естественно пиковая амплитуда сигнала  зависит от типа сигнала, но, как правило, в среднем
зависит от типа сигнала, но, как правило, в среднем 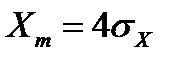 . В этом случае выражение примет вид:
. В этом случае выражение примет вид:


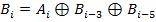 .
. - двоичная цифра результирующего кода, полученная на i-м такте работы скремблера,
- двоичная цифра результирующего кода, полученная на i-м такте работы скремблера,  - двоичная цифра исходного кода, поступающая на i-м такте на вход скремблера,
- двоичная цифра исходного кода, поступающая на i-м такте на вход скремблера,  и
и  - двоичные цифры результирующего кода, полученные на предыдущих тактах работы скремблера (соответственно на 3 и на 5 тактов ранее текущего такта) и объединенные операцией исключающего ИЛИ (сложение по модулю 2).
- двоичные цифры результирующего кода, полученные на предыдущих тактах работы скремблера (соответственно на 3 и на 5 тактов ранее текущего такта) и объединенные операцией исключающего ИЛИ (сложение по модулю 2).

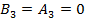

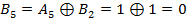
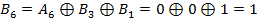





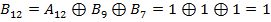
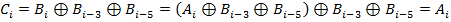

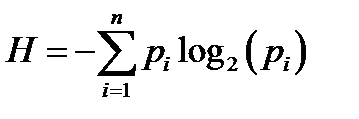
 - вероятность i-го выходного значения и
- вероятность i-го выходного значения и  . Если сообщение двоичное или источник имеет только два возможных выходных значения с вероятностями
. Если сообщение двоичное или источник имеет только два возможных выходных значения с вероятностями  и
и  , выражение для энтропии примет следующий вид:
, выражение для энтропии примет следующий вид:
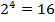 . Полученные величины нормируются и определяются их вероятности. По формуле 3 рассчитывается энтропия. В качестве параметров энтропии выбираются вероятности появления 4-х битовых слов, состоящих только из 0, а также только из 1.
. Полученные величины нормируются и определяются их вероятности. По формуле 3 рассчитывается энтропия. В качестве параметров энтропии выбираются вероятности появления 4-х битовых слов, состоящих только из 0, а также только из 1. с периодом Т может быть разложена в ряд (возможно, бесконечный), состоящий из сумм синусов и косинусов, имеющих различные частоты и амплитуды. Подобное разложение называется рядом Фурье. Разложенная в ряд Фурье функция может быть восстановлена по элементам этого ряда, то есть если период Т и амплитуды гармоник известны, то исходная функция может быть восстановлена с помощью суммы этих гармонических составляющих.
с периодом Т может быть разложена в ряд (возможно, бесконечный), состоящий из сумм синусов и косинусов, имеющих различные частоты и амплитуды. Подобное разложение называется рядом Фурье. Разложенная в ряд Фурье функция может быть восстановлена по элементам этого ряда, то есть если период Т и амплитуды гармоник известны, то исходная функция может быть восстановлена с помощью суммы этих гармонических составляющих.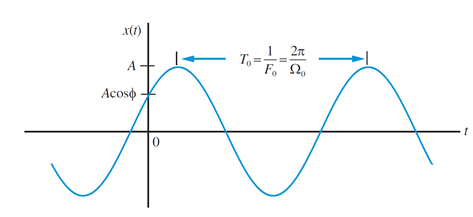
 можно разложить на бесконечные последовательности синусоидальных и косинусоидальных функций:
можно разложить на бесконечные последовательности синусоидальных и косинусоидальных функций:

 и
и  можно определить, решив следующие выражения:
можно определить, решив следующие выражения: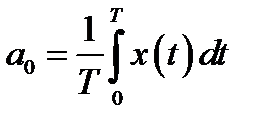


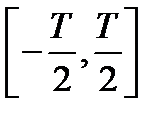 . Любая функция, разлагаемая в ряд Фурье, должна отвечать условиям Дирихле: быть ограниченной, кусочно-непрерывной и имеющей на протяжении периода конечное число экстремумов.
. Любая функция, разлагаемая в ряд Фурье, должна отвечать условиям Дирихле: быть ограниченной, кусочно-непрерывной и имеющей на протяжении периода конечное число экстремумов. содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами
содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами  (n=1,2,…), кратными основной частоте последовательности. Можно показать, что имеет место равенство
(n=1,2,…), кратными основной частоте последовательности. Можно показать, что имеет место равенство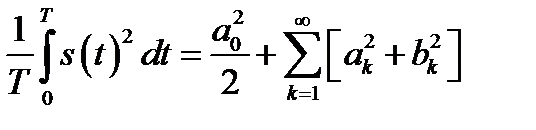
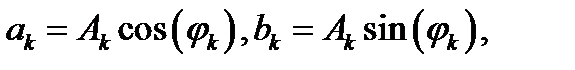



 ,
,  ,
,  ,…,
,…,  ,…, по оси ординат – соответствующие значения амплитуд A1, A2, A3,…, Ak,…. При этом считаем, что постоянной составляющей периодического колебания A0 соответствует частота
,…, по оси ординат – соответствующие значения амплитуд A1, A2, A3,…, Ak,…. При этом считаем, что постоянной составляющей периодического колебания A0 соответствует частота  = 0.
= 0.