
|
|
Исчисление высказываний ИВВсякую математическую теорему можно записать в виде импликации, выделив условие и заключение. При доказательстве теоремы из ее условия по определенным правилам получают заключение, при этом говорят, что заключение является логическим следствием условия или что оно выводимо из условия. Алгебра высказываний дает точное определение понятия выводимости. Однако чтобы непосредственно применять алгебру высказываний к высказываниям математики, нужно предположить, что для каждого высказывания выполняется закон исключенного третьего. Поэтому возникла необходимость в построении математической логики, как формально-аксиоматической (синтаксической) теории, которая ставит себе, в частности, задачу обосновать этот закон, доказав, что использование его не приводит к противоречию. Такой аксиоматической теорией, адекватной алгебре высказываний, является исчисление высказываний. Исчисление высказываний – это аксиоматическая логическая система, адекватная алгебре высказываний. Опишем это исчисление. В качестве алфавита исчисления высказываний возьмем следующее множество символов: 1) счетное множество высказывательных переменных, обозначаемых прописными латинскими буквами с индексами и без них; 2) символы логических операций 3) скобки ( , ). Вместе с символами алфавита будем использовать и метасимволы: латинские буквы жирного шрифта для обозначения формул и знак = для обозначения формул метасимволами. Множество формул обычно задается индуктивным определением. Допустимыми последовательностями символов или словами в языке исчисления высказываний являются формулы алгебры высказываний. Пункты 1 и 2 этого определения определяют элементарные формулы, а п. 3 – механизм образования новых формул. Следует заметить, что в исчислении высказываний не разрешается опускать скобки для операций с большим приоритетом, что допустимо в алгебре высказываний. Так, например, формула алгебры высказываний Следующим шагом в описании исчисления высказываний будет выделение класса формул, которые будем называть истинными или доказуемыми в исчислении высказываний. Это определение имеет такой же рекуррентный характер, как и определение формулы. Сначала определим исходные истинные формулы, называемые аксиомами. В качестве системы аксиом примем следующие формулы (аксиоматика П.С.Новикова). 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. После этого определим правила, позволяющие из истинных формул образовывать новые. Эти правила, мы будем называть правилами вывода. Образование истинной формулы из исходных истинных формул или аксиом путем применения правил вывода будем называть выводом данной формулы из аксиом. Определим правила вывода, которые являются отношениями на множестве формул. 1. Правило подстановки. Пусть U– формула, содержащая высказывательную переменную A. Тогда если U – истинная формула в исчислении высказываний, то, заменяя в ней переменную A всюду, куда она входит, произвольной формулой B, мы также получим истинную формулу. 2. Правило заключения (modus ponens). Если U и U®B истинные формулы в исчислении высказываний, то B также истинная формула. В виде схемы правило заключения запишется как
Задание 1. Показать, что формулы: 1) 2) истинны в исчислении высказываний. Решение. 1) Формула является результатом подстановки в аксиому 2 высказывательной переменной A вместо C. Так как посылка полученного следования есть аксиома 1, то, применяя правило заключения, получим, что
истинная формула. 2) В соответствии с правилом подстановки, заменив все вхождения переменной A в аксиоме 5 на формулу
Так как посылка этой аксиомы является аксиомой 4, то по правилу заключения формула
является истинной формулой. Заменим в этой формуле высказывательную переменную C на A
Снова воспользовавшись правилом заключения, что возможно, так как посылка истинной формулы является аксиомой 3, получим требуемую формулу
Замечание. Рассмотренная нами аксиоматика не является единственно возможной. Приведем и другие, эквивалентные данной, системы аксиом. I. Операции: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. II. Операции: 1. 2. 3. III. Операции: 1. 2. 3. 4. IV. Операции: Ø, ® (аксиоматика Лукасевича). 1. 2. 3. Рассмотрим пример вывода формулы. Задание 2. Доказать, что Aú- Решение. Для данного примера система посылок содержит 1 формулу U1=A, а выводимая формула B = 1) B1 =A 2) B2 = 3) B3 = B = Заметим, что если посылки являются аксиомами или теоремами исчисления высказываний, то класс выводимых из них формул совпадает с классом всех истинных формул, выводимых из любой системы посылок. Выводимость формулы из системы посылок отличается от доказательства теоремы в исчислении высказываний тем, что здесь допускается использование только правила заключения. Но при выводе формулы разрешается использовать любую теорему исчисления высказываний, для получения которой может применяться правило подстановки. Из каждой формулы U с помощью правила подстановки, производящего замену высказывательных переменных в этой формуле любыми формулами, может быть получено бесконечное множество формул. Это множество формул называется схемой формулы U и обозначается выражением, полученным заменой в формуле U всех входящих в нее высказывательных переменных Например, из формулы
возникает схема формул
Этой схеме принадлежит формула
Новые схемы формул можно получить заменой ее метасимволов схемами формул. Эти схемы выделяют некоторое подмножество формул из множества формул, принадлежащих исходной схеме. Например, из схемы (5) можно получить схему формул
Формула Для формул, являющимися аксиомами или теоремами, схемы формул называются соответственно схемами аксиом или схемами теорем. Схемами аксиом являются: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Таким образом, при выводе формулы из системы посылок (которая может быть и пустой) будут использоваться схемы аксиом и правило заключения, правило подстановки применяется неявно в схеме аксиом. Наряду с правилом заключения, мы будем использовать и другие правила образования истинных и выводимых формул. Эти правила являются производными от основных и используются для сокращения многократного применения основных правил. Перечислим основные из производных правил вывода. Как и прежде, метасимволы 1. Правило повторения посылки. T, 2. Правило введения посылки. ЕслиTú- 3. Правило удаления посылки. Если T, 4. Правило силлогизма. ЕслиTú- 5. Правило введения импликации. ЕслиT, Это весьма важное свойство называют еще теоремой дедукции. Учитывая, что Теорема дедукции. Если
то
6. Правило удаления импликации. ЕслиTú- 7. Правило введения конъюнкции. T, 8. Правило удаления конъюнкции. T, T, 9. Правило введения дизъюнкции. T, T, 10. Правило удаления дизъюнкции. Если T, 11. Правило введения отрицания. Если T, 12. Правило удаления отрицания. T, 13. Правило контрапозиции. Если T, Правила 1-13 называют обычно правилами естественного вывода, а вывод формулы из системы посылок, при котором используются эти правила, - естественным выводом. Эти правила также можно записывать в виде схемы. Обозначим через
¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾
назовем допустимым в исчислении высказываний правилом, если в исчислении высказываний из Рассмотрим примеры вывода формул с использованием правил естественного вывода. Несложно доказать, таким образом, справедливость основных эквивалентностей алгебры высказываний. Всюду далее, строя вывод формулы, будем рядом с каждой формулой последовательности указывать применяемое правило (его номер), а затем, в круглых скобках, номера формул исходных посылок, к которым применялось данное правило. Задание 3. Доказать выводимость формул закона двойственности: 1) ú- 2) ú- Решение. Покажем вначале справедливость формулы 1).
Построим теперь обратный вывод.
Выводить, как уже отмечалось, можно не только ТИ-формулы (теоремы исчисления высказываний), но и формулы, которые будут истинными при условии истинности системы посылок. Рассмотрим пример такого вывода. Задание 4. Доказать, что
Решение. Построим вывод этой формулы.
При выводе формул широко используются свойства монотонности конъюнкции, дизъюнкции и импликации. Теорема 2.1. Имеют место следующие выводимости: 1) 2) 3) Следствие. Если 1) 2) 3)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; не является формулой исчисления высказываний, ее следует записать, как
не является формулой исчисления высказываний, ее следует записать, как  , в дальнейшем изложении мы будем опускать лишь внешние скобки.
, в дальнейшем изложении мы будем опускать лишь внешние скобки.


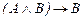
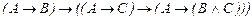





 .
. ;
;

 , получим
, получим .
.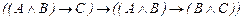
 .
. .
. (аксиоматика С.Клини (1952)).
(аксиоматика С.Клини (1952)).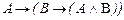
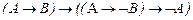
 (аксиоматика Россера (1953)).
(аксиоматика Россера (1953)).
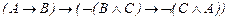
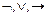 (аксиоматика Д.Гильберта и Аккермана (1938)).
(аксиоматика Д.Гильберта и Аккермана (1938)).



 .
.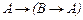 - аксиома 1
- аксиома 1 метасимволами
метасимволами  .
.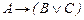
 . (5)
. (5)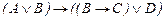 .
.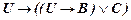 . (6)
. (6)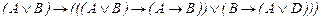 принадлежит как схеме формул (5), так и (6).
принадлежит как схеме формул (5), так и (6).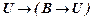

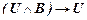





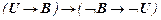

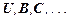 являются произвольными формулами, а через T обозначим конечное множество формул (возможно пустое).
являются произвольными формулами, а через T обозначим конечное множество формул (возможно пустое). ú-
ú-  ú-
ú-  , . . . ,Tú-
, . . . ,Tú-  и
и  ú-
ú- 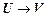 .
. - конечное множество формул, свойство 5 можно сформулировать в следующем виде:
- конечное множество формул, свойство 5 можно сформулировать в следующем виде: ú- B,
ú- B, ú-
ú- 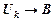 .
. ú-
ú- 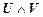 .
.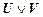 ,
, ú-
ú-  ú-
ú-  , то Tú-
, то Tú-  .
.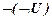 ú-
ú- 
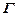 – систему посылок
– систему посылок  . Выражение вида
. Выражение вида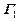 ú-U1, . . . ,
ú-U1, . . . ,  ú- Un
ú- Un ;
;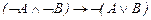 .
.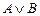
 ú-
ú- 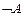


 ú-
ú- 
 ú-
ú- 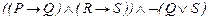 ú-
ú- 



 ú-
ú- 
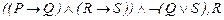 ú-
ú- 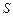




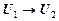 ,
,  ú-
ú-  ;
; ;
; .
.