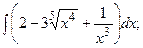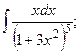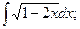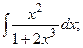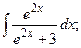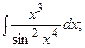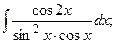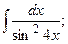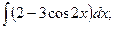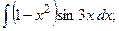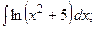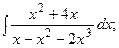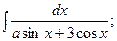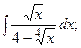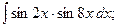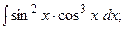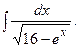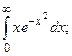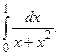|
|
Найдем интегралы (м – н) методом интегрирования по частям,Таблица основных интегралов
СПИСОК ЛИТЕРАТУРЫ 1. Бугров Я.С., Никольский С.М. Высшая математика: Учеб. для вузов: в 3т.-5-е изд., стер. - М.: Дрофа .- (Высшее образование. Современный учебник). Т.2. Дифференциальное и интегральное исчисление. - 2003. - 509 с. 2. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие. - 22-е изд., перераб.- СПб: Профессия, 2003. - 432 с. 3. Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я.-6-е изд.-М.: ОНИКС 21 век, ч.2. -2002.-416 с. 4. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. пособие: в 2-х т.- Изд. стер. –М.: Интеграл – Пресс. Т.1. -2001.- 415 с. 5. Письменный Д.Т. Конспект лекций по высшей математике, 1 часть. – 2-е изд., испр. – М.: Айрис-пресс, 2002. – 288 с.: ил.
Образец решения варианта
Задание 1: Вычислить интеграл:
Решение: а) Найдем интеграл, применив свойства неопределенного интеграла и формулы (1) и (2) табличного интегрирования:
Интегралы (б – л) решим методом замены переменной.
б) {для нахождения интеграла применим формулу (2)}
в) {для нахождения интеграла применим формулу (12)}
г) {для нахождения интеграла применим формулу (4)}
д) {для нахождения интеграла применим формулу (2)}
е) {для нахождения интеграла применим формулу (5)}
ж) {для нахождения интеграла применим формулу (8)}
з) {для нахождения интеграла применим формулу (10)}
и) {для нахождения интеграла применим формулу (9)}
к) {для нахождения интеграла применим формулу (3)}
л) {для нахождения интеграла применим формулу (7)}
Найдем интегралы (м – н) методом интегрирования по частям, используя формулу
м)
{для нахождения интеграла применим формулу (6)}
н) {второе слагаемое вычислим с помощью замены, применив формулу (2)}
в итоге получаем
о) Под знаком интеграла правильная рациональная дробь. Разложим её на простейшие дроби:
Перейдем к равенству числителей:
Отсюда следует, что
Тогда Интегрируя почленно полученное равенство и применяя свойства неопределённого интеграла, получим:
{для нахождения интегралов применим формулу (3)}
п) Под знаком интеграла неправильная рациональная дробь. Выделим целую часть этой дроби путем деления числителя на знаменатель:
Выделим полный квадрат в знаменателе правильной рациональной дроби:
Возвращаясь к исходному интегралы, получим:
р) Найдем интеграл используя универсальную тригонометрическую подстановку:
Разложим подынтегральную функцию на простейшие дроби:
Перейдем к равенству числителей:
Отсюда следует, что
Тогда Интегрируя почленно полученное равенство, получим::
{для нахождения интегралов применим формулу (3)}
с) Произведем замену: Получим: Наименьшее общее кратное знаменателей дробей
{для нахождения интегралов применим формулы (1) и (3)}
т) Найдем интеграл, используя формулу тригонометрических преобразований Интегрируя почленно полученное равенство и применяя формулу (6), получим:
у)
{для нахождения интегралов применим формулы (1) и (6)}
ф)
{для нахождения интеграла применим формулу (7)}
Задание 2: Вычислить несобственные интегралы или установить их расходимость.
Решение: а) Несобственный интеграл I рода.
{для нахождения интеграла применим формулу (2)}
б) Несобственный интеграл II рода.
{для нахождения интеграла применим формулу (8)}
Задание 3:Вычислить: а) площадь фигуры, ограниченной линиями: б) длину дуги кривой:
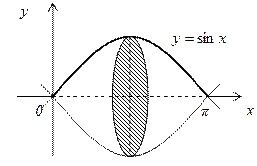
в) объем тела, полученного вращением фигуры
Решение: а) Существуют несколько формул для вычисления площадей плоских фигур.
§ Площадь фигуры, заданной в декартовой системе координат, ограниченной линиями
§
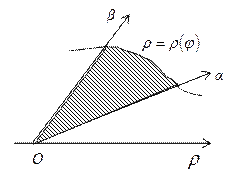
§ Площадь фигуры, заданной в полярной системе координат, ограниченной кривой
В нашем случае линии, ограничивающие фигуру, заданы в декартовых координатах, поэтому мы будем использовать формулу (14).
б) В зависимости от способа задания уравнения кривой существуют следующие формулы нахождения длины дуги кривой.
§ Для кривой, заданной в декартовых координатах уравнением
§ Для кривой, заданной параметрически уравнениями
§
В нашем случае кривая задана параметрически, поэтому для вычисления её длины мы применим формулу (18).
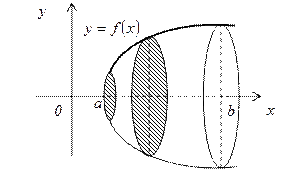
в) Пусть функция
Если криволинейная трапеция ограниченна графиком непрерывной функции
В условиях нашей задачи
Контрольная работа №7 Вариант 1.
Задание 1: Вычислить интегралы:
Задание 2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: а) площадь фигуры, ограниченной параболами: б) длину дуги кривой: в) объем тела, полученного вращением вокруг оси ОY фигуры, ограниченной гиперболой
Контрольная работа №7 Вариант 2.
Задание 1: Вычислить интегралы:
Задание 2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: а) площадь фигуры, заключенной между кривой б) длину дуги кривой в) объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной кривыми
Контрольная работа №7 Вариант 3.
Задание 1: Вычислить интегралы:
Задание 2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: а) площадь фигуры, ограниченной линией б) длину дуги кривой в) объем тела, полученного вращением вокруг оси
Контрольная работа №7 Вариант 4.
Задание 1: Вычислить интегралы:
Задание 2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: а) площадь фигуры, ограниченной кривой б) длину одной арки циклоиды: в) объем тела, образованного вращением вокруг оси
Контрольная работа №7 Вариант 5.
Задание 1: Вычислить интегралы:
Задание2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: а) площадь фигуры, ограниченной гиперболой б) длину дуги одного оборота спирали Архимеда в) объем тела, образованного вращением вокруг оси
Контрольная работа №7 Вариант 6.
Задание 1: Вычислить интегралы:
Задание 2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: а) площадь фигуры, ограниченной линиями б) длину дуги кривой в) объем тела, полученного вращением вокруг оси
Контрольная работа №7 Вариант 7.
Задание 1: Вычислить интегралы:
Задание 2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: а) площадь фигуры, ограниченной параболой б) длину дуги полукубической параболы в) объем тела, полученного вращением вокруг оси
Контрольная работа №7 Вариант 8.
Задание 1: Вычислить интегралы:
Задание 2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: а) площадь фигуры, ограниченной параболами: б) длину дуги полукубической параболы в) объём тела, образованного вращением фигуры, ограниченной линиями
Контрольная работа №7 Вариант 9.
Задание 1: Вычислить интегралы:
Задание 2: Вычислить несобственные интегралы или установить их расходимость:
Задание 3: Вычислить: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
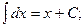
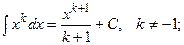
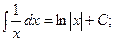
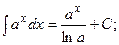 4а
4а 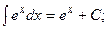
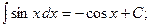
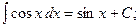
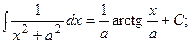
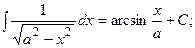
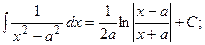
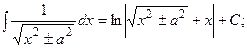
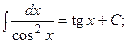
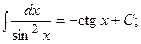
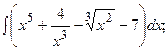
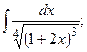
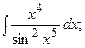
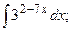

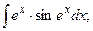
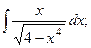
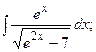
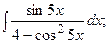
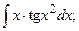

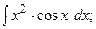
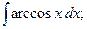
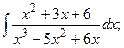
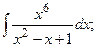
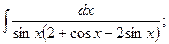
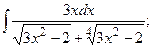
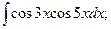
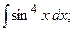
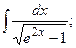
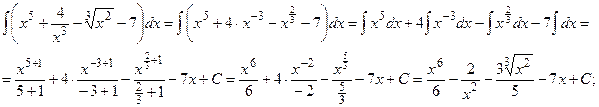
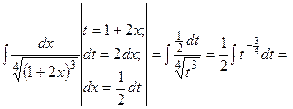
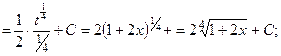
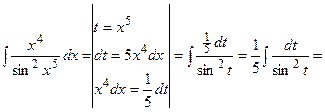


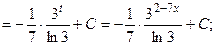
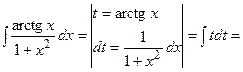
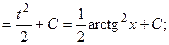

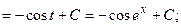
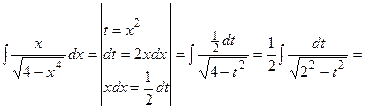
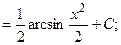
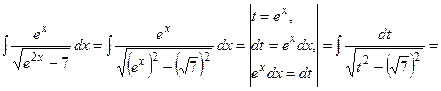
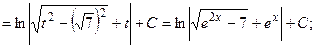
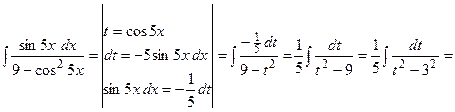
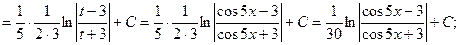
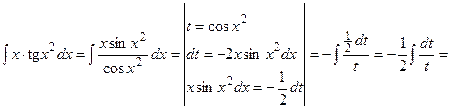
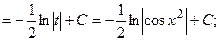
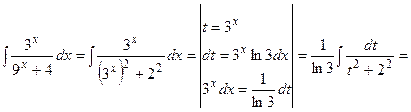
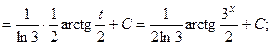
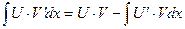 (13):
(13):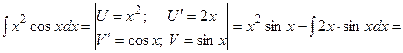

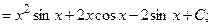
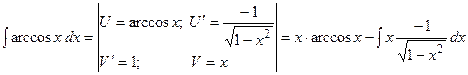
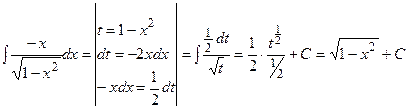
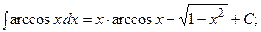
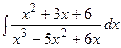 .
.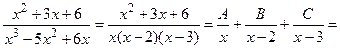
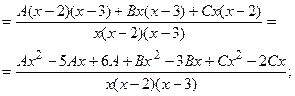
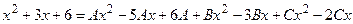 .
.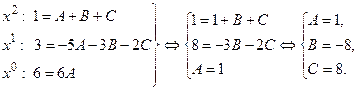
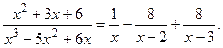
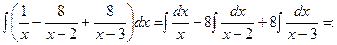
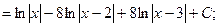
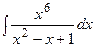 .
.
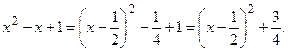
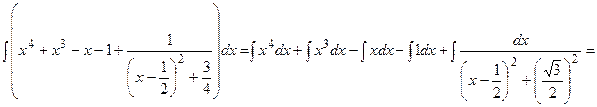 {для нахождения первых трёх интегралов применим формулу (2), для четвёртого – формулу (1), последний интеграл найдем c помощью формулы (7)}
{для нахождения первых трёх интегралов применим формулу (2), для четвёртого – формулу (1), последний интеграл найдем c помощью формулы (7)}
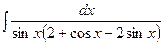 .
.
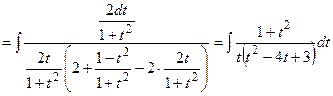 .
.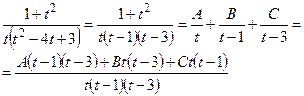
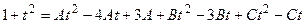 .
.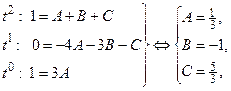
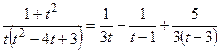 .
.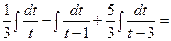
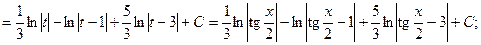
 .
.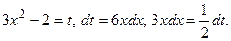
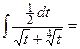
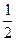 и
и 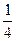 есть 4, поэтому введем следующую замену:
есть 4, поэтому введем следующую замену:
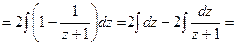
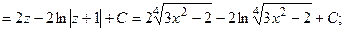
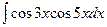 .
.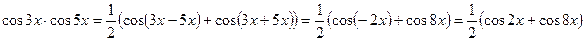
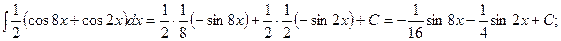
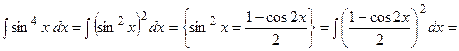
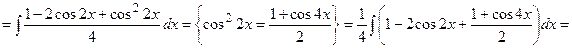
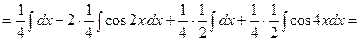
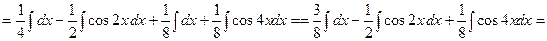
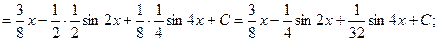 ;
;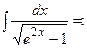



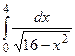

 - интеграл расходится.
- интеграл расходится.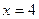 является точкой разрыва подынтегральной функции, поэтому:
является точкой разрыва подынтегральной функции, поэтому: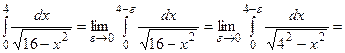
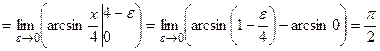 - интеграл сходится.
- интеграл сходится. и
и 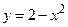 ;
;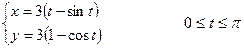 ,
,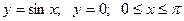 , вокруг оси
, вокруг оси 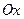 .
. 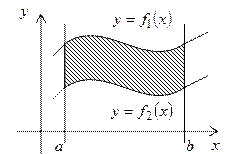
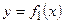 - сверху,
- сверху, 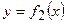 - снизу, слева прямой
- снизу, слева прямой 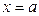 , справа прямой
, справа прямой  определяется формулой
определяется формулой 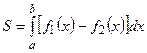 (14);
(14);
 Площадь фигуры, ограниченной кривой заданной параметрически уравнениями
Площадь фигуры, ограниченной кривой заданной параметрически уравнениями 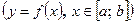
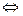
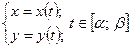 , определяется формулой
, определяется формулой  (15);
(15);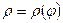 и лучами
и лучами 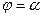 ,
, 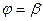 , определяется формулой:
, определяется формулой: 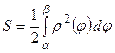 (16).
(16).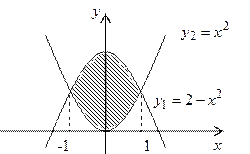 Найдем координаты точек пересечения линий:
Найдем координаты точек пересечения линий: 

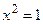
 ;
; 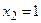
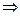
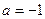 ;
;  .
.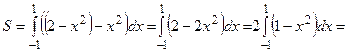
 ;
;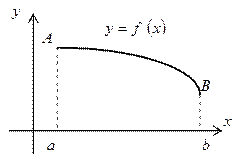
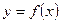
 длина дуги находится по формуле
длина дуги находится по формуле 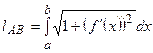 (17);
(17);
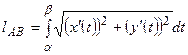 (18);
(18);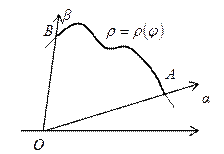 Для кривой, заданной в полярных координатах уравнением
Для кривой, заданной в полярных координатах уравнением  длина дуги находится по формуле
длина дуги находится по формуле 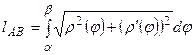 (19).
(19).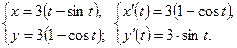
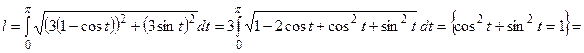
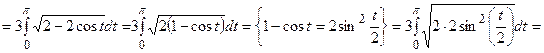
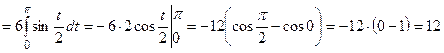 ;
;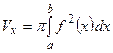 (20).
(20).

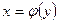 и прямыми
и прямыми 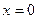 ,
, 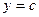 ,
, 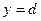
 , то объём тела, образованного вращением этой трапеции вокруг оси
, то объём тела, образованного вращением этой трапеции вокруг оси  , по аналогии с формулой (20), равен:
, по аналогии с формулой (20), равен: 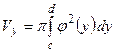 (21).
(21).
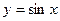 ,
,  ,
, 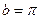 .
.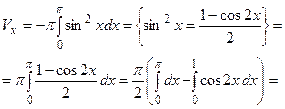 .
.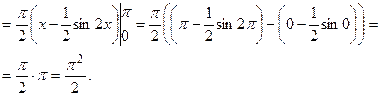
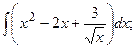
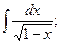
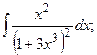
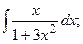
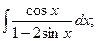

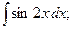
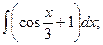
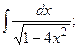
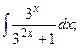

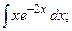
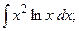

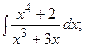
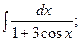

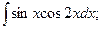
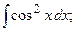
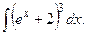

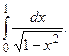
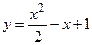 и
и 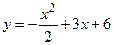 ;
; от точки с абсциссой
от точки с абсциссой 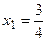 до точки
до точки 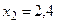 ;
; , осью ОY и прямыми
, осью ОY и прямыми 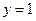 и
и 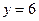 .
. 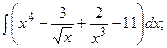
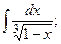
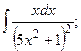
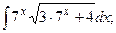

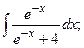
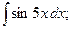
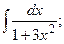
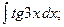

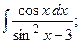
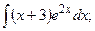

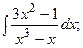
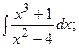
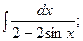
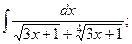
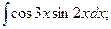

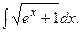
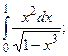
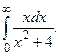
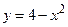 и осью
и осью 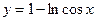 в пределах от
в пределах от 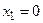 до
до  ;
;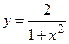 .
.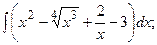
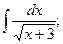
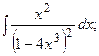
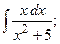
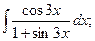
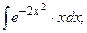
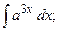
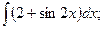
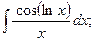
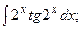
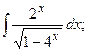
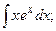
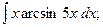

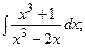
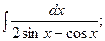
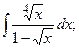
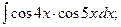
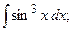
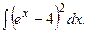
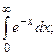

 , осью
, осью 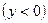 ;
;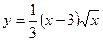 между точками пересечения её с
между точками пересечения её с 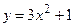 и прямой
и прямой 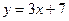 .
. 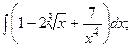
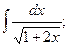

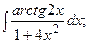
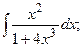
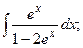

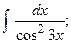
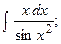
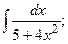
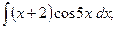


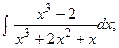

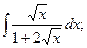
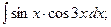
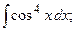
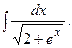
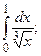
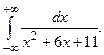
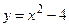 и прямыми
и прямыми 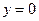 ,
, 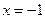
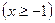 ;
;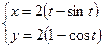 ;
;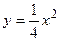 , прямой
, прямой 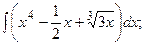
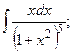
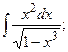
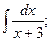

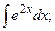

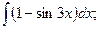
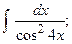

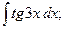
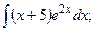
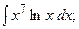

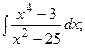
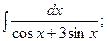
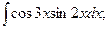
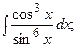
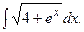
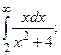

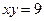 , осью ОХ и прямыми
, осью ОХ и прямыми 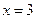 и
и 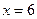 ;
;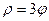 ;
;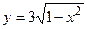 , параболой
, параболой 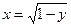 и осью
и осью 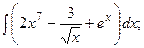
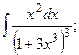

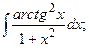
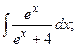
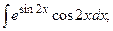
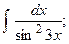
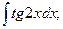
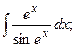
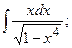
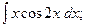
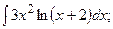
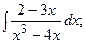
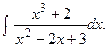
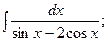
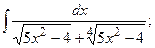
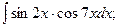

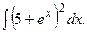
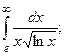
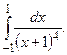
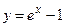 ,
, 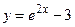 и осью
и осью  от
от 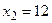 ;
;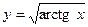 и прямыми
и прямыми 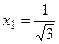 и
и 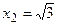 .
. 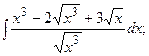
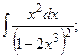

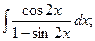
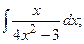

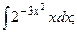


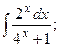
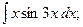
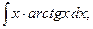

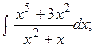


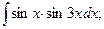
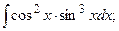
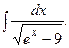
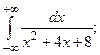
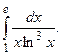
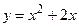 и прямой
и прямой 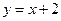 ;
;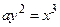 от начала координат до точки с абсциссой
от начала координат до точки с абсциссой  ;
;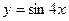 и осью
и осью 
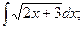

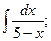
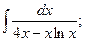
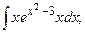

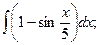
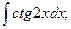

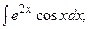

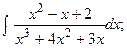
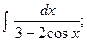
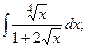
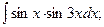
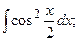
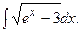

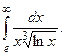
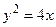 и
и 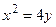 ;
;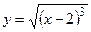 от точки
от точки 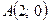 до точки
до точки 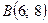 ;
;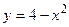 ,
, 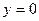 ,
,