
|
|
ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ.12
Рассмотрим функцию:
Th.1 Пусть : 1. g(x) определена в 2. g(x) дифференцируема в точке 3. Тогда
Доказательство: а) пусть n=1. g(x) дифференцируема в точке
Пусть
Т.к.
=
б) n>1. Это частный случай пункта а), т.к. рассматриваемая функция
Выпишем формулу (1) для всех частных случаев: n=1, k=2:
ПРИМЕР.
n=2, k=2:
Пусть
ПРИМЕР.
df.1 Пусть
Доказательство формулы следует из Th.1 при Th.2 (Инвариантность формы записи первого дифференциала) Пусть y=g(x) – дифференцируема в точке 1. Сложная функция y=g(x(t))=F(t) – дифференцируема в точке 2. ЗАМЕЧАНИЕ. Пусть функция f(x), Он будет функцией 2n переменных фиксированных а) б) в) Докажем б). Из Th о дифференцируемости сложной функции следует, что функция U(x)V(x) дифференцируема, если дифференцируемы U(x) и V(x). Далее имеем: = ПРИМЕР. Найти дифференциал функции Решение. Пусть
ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ. Пусть дана функция Пусть теперь для Аналогично. Частной производной порядка
Частная производная, полученная дифференцированием по различным переменным, называется смешанной. Например: Пусть Частные производные по x и y от функций
Аналогично определяются частные производные более высокого порядка. Для функции
ПРИМЕР.
Имеем: В этом примере смешанные частные производные равны друг другу. Вообще говоря, значения смешанных производных зависит от порядка, в котором производится последовательные дифференцирования. Нетрудно заметить, что число частных производных с увеличением порядка возрастает. Однако, некоторые из них при наличии условий совпадают. Th.1 Пусть Пусть смешанные частные производные m-го порядка непрерывны в точке Тогда смешанные частные производные порядка ”m” не зависят от порядка дифференцирования. (Б/Д). Следует отметить, что это условие достаточное. Перефразируем Th.1 для случая функции двух переменных. n=2 m=1: Пусть df.1 Пусть ПРИМЕР.
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ. Пусть
Вторым дифференциалом функции f в точке 1) дифференциалы независимых переменных 2) И старые приращения
df.2 Дифференциалом порядка “m” функции f в точке называется дифференциал от дифференциала порядка “m-1” при тех же предположениях, что и в предыдущем определении. Th.2 Пусть функция
СЛЕДСТВИЕ. (n=2) Пусть
(Б/Д). В частности если функция
= ЗАМЕЧАНИЕ. Если ввести формально дифференциальный оператор:
то выражение для дифференциалов можно записать в удобной символической форме:
Под произведением дифференциальных операторов понимается их последовательное применение. Например, если
ЗАМЕЧАНИЕ. Для дифференциалов высших порядков инвариантность формы записи не сохраняется. Th.3 (Формула Тейлора) Пусть функция
Следует иметь ввиду Если n=2
+
Следует иметь ввиду:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
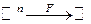

 , функция f(t) определена в
, функция f(t) определена в  , где
, где  .
.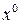 (т.е.
(т.е.  ).
).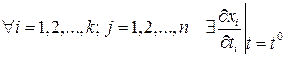
 :
: (1)
(1)
 ,
,  . Причем
. Причем .
.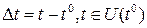 при
при  :
: (*)
(*) непрерывна в точке
непрерывна в точке 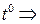 при
при . Кроме того
. Кроме того 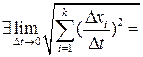
 переходим к пределу в (*)при
переходим к пределу в (*)при  :
:
 т.е. имеем y=g(x).
т.е. имеем y=g(x). , т.к.
, т.к.  ч. и т. д.
ч. и т. д.

 .
. 




 , где
, где 
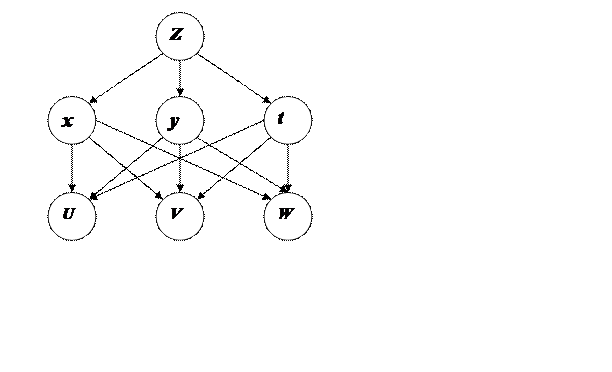



 .
. ,
, и удовлетворяет условиям Th.1 в точке
и удовлетворяет условиям Th.1 в точке  . Тогда
. Тогда 
 - полная производная.
- полная производная. . При
. При 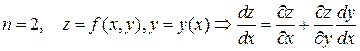 .
. - дифференцируема в точке
- дифференцируема в точке  .
. (Б/Д).
(Б/Д). дифференцируема во всех точках некоторого открытого множества
дифференцируема во всех точках некоторого открытого множества  . Тогда в каждой точке
. Тогда в каждой точке  можно вычислить дифференциал:
можно вычислить дифференциал:  .
. причем при
причем при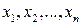 дифференциал есть линейная функция
дифференциал есть линейная функция  . Правила дифференцирования такие же, как и для функции одной переменной.
. Правила дифференцирования такие же, как и для функции одной переменной.

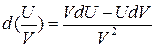 , если
, если  .
. =
= .
. .
. , тогда:
, тогда:
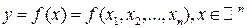 . Определенные ранее частные производные
. Определенные ранее частные производные  называют также частными производными первого порядка.
называют также частными производными первого порядка. -ет частная производная по
-ет частная производная по  в точке
в точке  . Тогда
. Тогда  называют частными производными второго порядка.
называют частными производными второго порядка. называется частная производная (по любой переменной
называется частная производная (по любой переменной  .
.
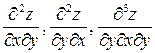 и т.д.
и т.д. , т.е.
, т.е.  - определена в некоторой области E.
- определена в некоторой области E.  - также являются функциями двух переменных и определены в области E или ее части.
- также являются функциями двух переменных и определены в области E или ее части.

 , f определена в области E, z=f(x,y) –частные производные третьего порядка определяются формулами:
, f определена в области E, z=f(x,y) –частные производные третьего порядка определяются формулами:
 .
.
 ,
,  ,
,  ,
,  .
. определена вместе со своими частными производными в окрестности
определена вместе со своими частными производными в окрестности  до порядка ”m”.
до порядка ”m”. определены в точке
определены в точке 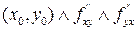 непрерывны в точке
непрерывны в точке 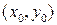 . Тогда, частные производные
. Тогда, частные производные  . (Б/Д).
. (Б/Д). .
. .
.

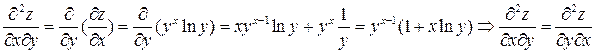 .
. и f дифференцируема в окрестности точки
и f дифференцируема в окрестности точки 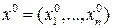 . Рассмотрим дифференциал:
. Рассмотрим дифференциал: - это дифференциал первого порядка.
- это дифференциал первого порядка. при вычислении вторых дифференциалов остаются постоянными.
при вычислении вторых дифференциалов остаются постоянными.
 , тогда
, тогда  :
: (Б/Д).
(Б/Д). , тогда
, тогда  :
: , где
, где 
 имеет непрерывные частные производные до второго порядка включительно, то, воспользовавшись теоремой о равенстве смешанных производных, получаем:
имеет непрерывные частные производные до второго порядка включительно, то, воспользовавшись теоремой о равенстве смешанных производных, получаем:
 .
. (1)
(1)
 , то
, то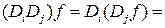
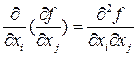 (2)
(2) ; При применении дифференциальных операторов вида (1) нужно пользоваться правилом (2). При этом дифференциалы независимых переменных
; При применении дифференциальных операторов вида (1) нужно пользоваться правилом (2). При этом дифференциалы независимых переменных 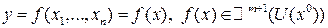
 Справедлива формула Тейлора:
Справедлива формула Тейлора:
 , где
, где  .
.
 . (Б/Д).
. (Б/Д). , тогда
, тогда  справедлива формула Тейлора:
справедлива формула Тейлора:
 .
. . Если
. Если 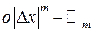 - в форме Пеано.
- в форме Пеано. , где
, где .
.