
|
|
Теорема Лагранжа о конечном приращении функции12 Теорема Лагранжа. Если функция Д о к а з а т е л ь с т в о. Составим вспомогательную функцию y = F(x), которая будет удовлетворять условиям теоремы Ролля.
Здесь
Рис. 27 Очевидно, что функция y = F(x) является непрерывной на отрезке Покажем, что функция y = F(x) принимает равные значения в граничных точках отрезка
Следовательно, функция y = F(x) удовлетворяет всем условиям теоремы Ролля и поэтому найдется такая внутренняя точка отрезка
Значение производной функции в точке х = с равно
Отсюда получаем
Часто рассматривают функцию y = f(x) на отрезке
Геометрический смысл теоремы Лагранжа На основании формулы
Теорема Коши Теорема Коши. Если функции y = f(x) и y = g(x) непрерывные на отрезке
Д о к а з а т е л ь с т в о. Очевидно, что Составим вспомогательную функцию y = F(x), которая будет удовлетворять условиям теоремы Ролля.
Значения функции y = F(x) в точках х = а и х = b равны нулю. Действительно,
Функция y = F(x) является дифференцируемой, так как является линейной комбинацией дифференцируемых функций y = f(x) и y = g(x). Находим
По теореме Ролля существует точка
Отсюда получаем
Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя Теорема 2.1.Если в некоторой окрестности точки
если этот предел существует (конечный или бесконечный). Д о к а з т е л ь с т в о. Доопределим функции y = f(x) и y = g(x) так, что
Учитывая, что Так как при
Если в результате применения правила Лопиталя получается снова неопределенность типа Правило Лопиталя справедливо также в случае когда
Здесь производные от функций
Правило Лопиталя справедливо так же, если Покажем это. Преобразуем данный предел к пределу с неопределенностью типа
Имеем равенство
Пример 2.10. Пример 2.11. Пример 2.12. Если при нахождении пределов неопределенность имеет вид произведения Пример 2.13.
Пример 2.14.
Если при применении правила Лопиталя под пределом имеются некоторые функции, которые не приводят к неопределенности, то эти функции нужно выделить в отдельный предел, т. е. разбить предел на два предела.
Пример 2.15.
Применение правила Лопиталя 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 непрерывна на отрезке
непрерывна на отрезке  и дифференцируемая в каждой его внутренней точке, то на интервале (a, b) найдется такая точка х = с, что
и дифференцируемая в каждой его внутренней точке, то на интервале (a, b) найдется такая точка х = с, что  .
. .
. - уравнение хорды, стягивающей граничные точки A(a, f(a)) и B(b, f(b)) графика функции
- уравнение хорды, стягивающей граничные точки A(a, f(a)) и B(b, f(b)) графика функции  равняется разности ординаты
равняется разности ординаты  и ординаты касательной
и ординаты касательной  (
(  ).
).
 ;
; .
.
 .
. .
.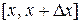 . В этом случае последняя формула имеет вид
. В этом случае последняя формула имеет вид Û
Û  .
. можно утверждать следующее.
можно утверждать следующее. Рис. 28
Рис. 28
 , то на этом интервале найдется такая точка
, то на этом интервале найдется такая точка  , в которой касательная параллельна хорде, стягивающей граничные точки графика функции (рис. 28).
, в которой касательная параллельна хорде, стягивающей граничные точки графика функции (рис. 28).
 ), то найдется такая внутренняя точка
), то найдется такая внутренняя точка  .
.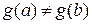 , иначе по теореме Ролля существовала бы такая точка
, иначе по теореме Ролля существовала бы такая точка  , что противоречит условию теоремы.
, что противоречит условию теоремы. .
. ,
, .
. .
. .
. функции y = f(x) и y = g(x) определены и дифференцируемые, причем
функции y = f(x) и y = g(x) определены и дифференцируемые, причем  , пределы функций при
, пределы функций при  равны нулю, т. е.
равны нулю, т. е.  , то предел отношения этих функций равняется пределу отношения их производных
, то предел отношения этих функций равняется пределу отношения их производных ,
, . Тогда на отрезке
. Тогда на отрезке  выполняются условия теоремы Коши, т. е. существует такая точка
выполняются условия теоремы Коши, т. е. существует такая точка  , что
, что .
. .
. , то
, то .
. и производные
и производные  и
и  также удовлетворяют требованиям теоремы, как функции
также удовлетворяют требованиям теоремы, как функции  , то можно повторно применить правило Лопиталя, т. е.
, то можно повторно применить правило Лопиталя, т. е. 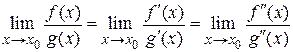 .
. . Покажем это. Пусть
. Покажем это. Пусть  . Сделаем замену переменной x = 1/t. Тогда при
. Сделаем замену переменной x = 1/t. Тогда при  и
и  ,
,  . Применим к функциям
. Применим к функциям  и
и  правило Лопиталя, получим
правило Лопиталя, получим .
. , т. е имеет место неопределенность типа
, т. е имеет место неопределенность типа  ,
,  .
.

 Отсюда получаем
Отсюда получаем 
 , т. е.
, т. е.  .
. .
. .
. .
. , то прежде, чем применять правило Лопиталя, ее нужно привести к неопределенностям типа частного
, то прежде, чем применять правило Лопиталя, ее нужно привести к неопределенностям типа частного  .
.
 .
.
 .
.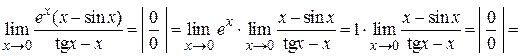

 .
.