Первый множитель в (3.3.10) обращается в нуль в точках, для которых
 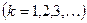 . (3.3.11) . (3.3.11)
В этих точках интенсивность, создаваемая каждой из щелей в отдельности, равна нулю (см. условие (3.3.4)).
Второй множитель в (3.3.10) принимает значение  в точках, удовлетворяющих условию в точках, удовлетворяющих условию
 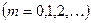 . (3.3.12) . (3.3.12)
Для направлений, определяемых этим условием, колебания от отдельных щелей взаимно усиливают друг друга вследствие чего амплитуда колебаний в соответствующей точке экрана равна
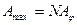 (3.3.13) (3.3.13)
 ( ( 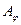 - амплитуда колебания, посылаемого одной щелью под углом - амплитуда колебания, посылаемого одной щелью под углом  ). ).
Условие (3.3.12) определяет положения максимумов интенсивности, называемых главными. Число  дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два. дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два.
Возведя равенство (3.3.13) в квадрат, получим, что интенсивность главных максимумов  в в  раз больше интенсивности раз больше интенсивности 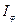 , создаваемой в направлении , создаваемой в направлении  одной щелью: одной щелью: 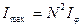 . .
Кроме минимумов, определяемых условием (3.3.11), в промежутках между соседними главными максимумами имеется  добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием
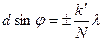 . (3.3.14) . (3.3.14)
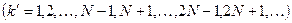 . .
В формуле (3.3.14) 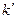 принимает все целочисленные значения, кроме принимает все целочисленные значения, кроме  , т. е. кроме тех, при которых условие (3.3.14) переходит в (3.3.12). , т. е. кроме тех, при которых условие (3.3.14) переходит в (3.3.12).
Условие (3.3.14) легко получить методом графического сложения колебаний. Колебания от отдельных щелей изображаются векторами одинаковой длины. Согласно (3.3.14) каждый из последующих векторов повернут относительно предыдущего на один и тот же угол
 . .
Поэтому в тех случаях, когда 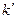 не является целым кратным не является целым кратным  , мы, пристраивая начало следующего вектора к концу предыдущего, получим замкнутую ломаную линию, которая делает , мы, пристраивая начало следующего вектора к концу предыдущего, получим замкнутую ломаную линию, которая делает 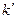 (при (при  ) или ) или 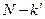 (при (при  ) оборотов прежде чем конец ) оборотов прежде чем конец  -го вектора упрется в начало 1-го. Соответственно результирующая амплитуда оказывается равной нулю. Сказанное пояснено на рис. 3.3.26, на котором показана сумма векторов для случая -го вектора упрется в начало 1-го. Соответственно результирующая амплитуда оказывается равной нулю. Сказанное пояснено на рис. 3.3.26, на котором показана сумма векторов для случая  и значений и значений 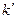 , равных , равных  и и  . .
Между дополнительными минимумами располагаются слабые вторичные максимумы. Число таких максимумов, приходящееся на промежуток между соседними главными максимумами, равно  . Ранее было показано, что интенсивность вторичных максимумов не превышает . Ранее было показано, что интенсивность вторичных максимумов не превышает  интенсивности ближайшего главного максимума. интенсивности ближайшего главного максимума.
 На рис. 3.3.27 приведен график функции (3.3.10) для На рис. 3.3.27 приведен график функции (3.3.10) для  и и  . Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на . Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на  . При взятом на рисунке отношении периода решетки к ширине щели . При взятом на рисунке отношении периода решетки к ширине щели  главные максимумы 3-го, 6-го и т. д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Вообще из формул (3.3.11) и (3.3.12) вытекает, что главный максимум главные максимумы 3-го, 6-го и т. д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Вообще из формул (3.3.11) и (3.3.12) вытекает, что главный максимум  -го порядка придется на -го порядка придется на  -й минимум от одной щели, если будет выполнено равенство: -й минимум от одной щели, если будет выполнено равенство:  , или , или 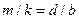 . Это возможно, если . Это возможно, если  равно отношению двух целых чисел равно отношению двух целых чисел  и и  (практический интерес представляет случай, когда эти числа невелики). Тогда главный максимум (практический интерес представляет случай, когда эти числа невелики). Тогда главный максимум  -го порядка наложится на -го порядка наложится на  -й минимум от одной щели, максимум -й минимум от одной щели, максимум  -го порядка - на -го порядка - на  -й минимум и т. д., в результате чего максимумы порядков -й минимум и т. д., в результате чего максимумы порядков  и т. д. будут отсутствовать. и т. д. будут отсутствовать.
Количество наблюдающихся главных максимумов определяется отношением периода решетки  к длине волны к длине волны  . Модуль . Модуль 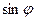 не может превысить единицу. Поэтому из формулы (3.3.12) вытекает что не может превысить единицу. Поэтому из формулы (3.3.12) вытекает что
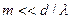 . .
Определим угловую ширину центрального (нулевого) максимума. Положение ближайших к нему дополнительных минимумов определяется условием  (см. формулу (3.3.14)), этим минимумам соответствуют (см. формулу (3.3.14)), этим минимумам соответствуют  = =  , при этом , при этом  , и угловая ширина центрального максимума равна , и угловая ширина центрального максимума равна  . .
Положение дополнительных минимумов, ближайших к главному максимуму  -го порядка, определяется условием: -го порядка, определяется условием: 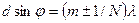 . Отсюда получается для угловой ширины . Отсюда получается для угловой ширины  -го максимума следующее выражение: -го максимума следующее выражение:
 . .
Обозначив 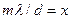 и и  , имеем , имеем
 . .
При большом числе щелей значение  будет очень мало, потому будет очень мало, потому 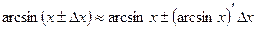 , и , и
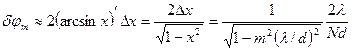 . .
При  
Произведение  дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума  ширина ширина  возрастает. возрастает.
В дифракционном спектре положение главных максимумов зависит от длины волны  . Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный - наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Стеклянная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, напротив, сильнее отклоняет красные лучи. . Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный - наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Стеклянная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, напротив, сильнее отклоняет красные лучи.
Основными характеристиками всякого спектрального прибора являются его дисперсия и разрешающая сила. Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на  ). Разрешающая сила определяет минимальную разность длин волн ). Разрешающая сила определяет минимальную разность длин волн  , при которой две линии воспринимаются в спектре раздельно. , при которой две линии воспринимаются в спектре раздельно.
Угловой дисперсией называется величина
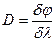 , ,
где  - угловое расстояние между спектральными линиями, отличающимися по длине волны на - угловое расстояние между спектральными линиями, отличающимися по длине волны на  . .
Чтобы найти угловую дисперсию дифракционной решетки, продифференцируем условие (3.3.12) главного максимума слева по  , а справа по , а справа по  . Опуская знак минус, получим . Опуская знак минус, получим
 . .
Отсюда
 . .
В пределах небольших углов  , поэтому можно положить , поэтому можно положить
 (3.3.15) (3.3.15)
- угловая дисперсия обратно пропорциональна периоду решетки  . Чем выше порядок спектра . Чем выше порядок спектра  , тем больше дисперсия. , тем больше дисперсия.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



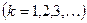 . (3.3.11)
. (3.3.11) в точках, удовлетворяющих условию
в точках, удовлетворяющих условию
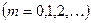 . (3.3.12)
. (3.3.12)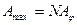 (3.3.13)
(3.3.13) (
( 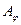 - амплитуда колебания, посылаемого одной щелью под углом
- амплитуда колебания, посылаемого одной щелью под углом  ).
). дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два.
дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два. в
в 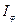 , создаваемой в направлении
, создаваемой в направлении 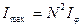 .
. добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием
добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием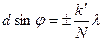 . (3.3.14)
. (3.3.14)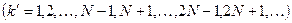 .
.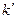 принимает все целочисленные значения, кроме
принимает все целочисленные значения, кроме  , т. е. кроме тех, при которых условие (3.3.14) переходит в (3.3.12).
, т. е. кроме тех, при которых условие (3.3.14) переходит в (3.3.12). .
. , мы, пристраивая начало следующего вектора к концу предыдущего, получим замкнутую ломаную линию, которая делает
, мы, пристраивая начало следующего вектора к концу предыдущего, получим замкнутую ломаную линию, которая делает  ) или
) или 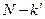 (при
(при  ) оборотов прежде чем конец
) оборотов прежде чем конец  и значений
и значений  и
и  .
. . Ранее было показано, что интенсивность вторичных максимумов не превышает
. Ранее было показано, что интенсивность вторичных максимумов не превышает  интенсивности ближайшего главного максимума.
интенсивности ближайшего главного максимума. На рис. 3.3.27 приведен график функции (3.3.10) для
На рис. 3.3.27 приведен график функции (3.3.10) для  и
и  . Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на
. Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на  главные максимумы 3-го, 6-го и т. д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Вообще из формул (3.3.11) и (3.3.12) вытекает, что главный максимум
главные максимумы 3-го, 6-го и т. д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Вообще из формул (3.3.11) и (3.3.12) вытекает, что главный максимум  -й минимум от одной щели, если будет выполнено равенство:
-й минимум от одной щели, если будет выполнено равенство:  , или
, или 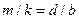 . Это возможно, если
. Это возможно, если  равно отношению двух целых чисел
равно отношению двух целых чисел  и
и  (практический интерес представляет случай, когда эти числа невелики). Тогда главный максимум
(практический интерес представляет случай, когда эти числа невелики). Тогда главный максимум  -го порядка - на
-го порядка - на  -й минимум и т. д., в результате чего максимумы порядков
-й минимум и т. д., в результате чего максимумы порядков  и т. д. будут отсутствовать.
и т. д. будут отсутствовать. к длине волны
к длине волны  . Модуль
. Модуль 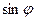 не может превысить единицу. Поэтому из формулы (3.3.12) вытекает что
не может превысить единицу. Поэтому из формулы (3.3.12) вытекает что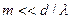 .
. (см. формулу (3.3.14)), этим минимумам соответствуют
(см. формулу (3.3.14)), этим минимумам соответствуют  , при этом
, при этом  , и угловая ширина центрального максимума равна
, и угловая ширина центрального максимума равна  .
.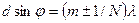 . Отсюда получается для угловой ширины
. Отсюда получается для угловой ширины  .
.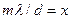 и
и  , имеем
, имеем .
. будет очень мало, потому
будет очень мало, потому 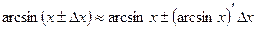 , и
, и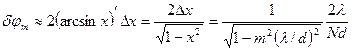 .
.

 дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума
дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума  возрастает.
возрастает. ). Разрешающая сила определяет минимальную разность длин волн
). Разрешающая сила определяет минимальную разность длин волн  , при которой две линии воспринимаются в спектре раздельно.
, при которой две линии воспринимаются в спектре раздельно.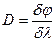 ,
, - угловое расстояние между спектральными линиями, отличающимися по длине волны на
- угловое расстояние между спектральными линиями, отличающимися по длине волны на  .
. .
. , поэтому можно положить
, поэтому можно положить (3.3.15)
(3.3.15)