
|
|
Элементарные функции алгебры логикиЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ Понятие множества является неопределяемым, оно считается интуитивно заданным. Каждое множество состоит из объектов, которые в дальнейшем называются элементами множества. Множества обычно обозначаются большими буквами: А, Х и т.д. Элементы же множеств, как правило, обозначают маленькими буквами: а, х и т.д. Для записи того, что а является элементом множества А, применяется значок Интуитивный принцип объемности Кантора: множества А и В считаются равными Пример. Рассмотрим множества: А = {множество всех положительных четных целых чисел}, В = {множество всех положительных целых чисел, представимых в виде суммы двух положительных нечетных целых чисел}, C = {2,4,6}, D = {2,6,4}. Из принципа объемности следует, что справедливы равенства А = В и С = D.● Для некоторых множеств существуют стандартные обозначения: Æ – пустое множество, т.е. множество, не имеющее ни одного элемента; N – множество натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; R – множество действительных чисел. Операции над множествами Определение. Говорят, что множество А включено в множество В, и пишут АÍВ, если для любого элемента аÎА справедливо аÎВ. Пример. Очевидны следующие включения N Операция включения множеств обладает следующими свойствами: 1о. Для любого множества А справедливо включение АÍА. 2о. Если АÍВ и ВÍА, то А = В. 3о. Если АÍВ и ВÍС, то АÍС. 4о. Для любого множества А справедливо включение ÆÍА. Замечание. Необходимо различать символ принадлежности Î и символ включения Í. Символ принадлежности не обязан удовлетворять тем же свойствам, что и символ включения. Так, например, 1 Î Z, Z Î {Z}, однако 1 Ï {Z}. 1. Объединением множеств А и В называется множество АÈВ, состоящее из тех элементов, которые принадлежат хотя бы одному из множеств А или В: АÈВ = {x 2. Разностью множеств А и В называется множество А\B, состоящее из тех и только тех элементов х, которые принадлежат множеству А и не принадлежат множеству В: А\B ={х 3. Пересечением множеств А и В называется множество АÇВ таких элементов х, которые принадлежат как множеству А, так и множеству В: АÇВ = {х Операции над множествами могут быть распространены на любое число множеств. Если ВÍА, то разность множеств А\B называют еще дополнительным множеством к В. Операции над множествами хорошо иллюстрируются диаграммами Венна.
Теорема. Для любых множеств A, B, C справедливы равенства
(Свойства 1, 2, 3, 1', 2', 3' называются соответственно свойствами ассоциативности, коммутативности и дистрибутивности). В случае, когда все рассматриваемые множества заведомо принадлежат одному и тому же множеству U, это множество называют универсумом. Множество U\А называется дополнением множества А и обозначается
Теорема. Для множеств
Пример. А Ç Æ= Æ Þ А È U = U; АÈÆ=А Þ А Ç U = А.● Произведение множеств Определение. Пусть А и В - множества. Произведением множеств А и В называется множество всех упорядоченных пар (а, в), где аÎА и вÎВ. Произведение обозначается А´В. А´В={(a,b) Произведение двух множеств часто называют прямым произведением. Заметим, что произведение n множеств А обозначается через Аn . Примеры.1) Если А = {a, b}, Е = {0, 1}, то А´Е = {(a, 0), (a, 1), (b, 0), (b, 1)}, Е´A ={(0, a) (0, b), (1, a), (1, b)}, 2) Пусть R´R. В этом случае получаем множество, обозначаемое R2 и являющееся плоскостью с декартовой системой координат (по этой причине произведение множеств часто называют декартовым произведением). 3) Пусть [a, b], [c, d] – отрезки прямой. Тогда [a, b]´[c, d] – прямоугольник на плоскости.● Основные понятия комбинаторики Комбинаторика–раздел математики, изучающий способы подсчета числа элементов в конечных множествах. Пусть 1. Система подмножеств множества Пример.
Число подмножеств равно 2. Размещение элементов из Пример.
Число размещений равно 3. Перестановки элементов множества Пример.
Число перестановок равно 4. Сочетание элементов из Пример.
Число сочетаний равно 5. Разбиение множества 1) 2) Правило произведения. Если объект Правило суммы. Если объект ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ Элементарные функции алгебры логики Введем обозначения Определение. Всюду определённой булевой функцией назовём отображение
Так как множество Пример. Пусть Тем самым задана функция
Таблица, задающая функцию Функции одной переменной: 1.
2.
3.
4.
Если стандартным расположением переменной x считать 0 в первой строке и 1 во второй, то функции f0, f1, f2, f3 определяются однозначно наборами значений: f0=(0, 0), f1=(0, 1), f2=(1, 0) и f3=(1, 1). Наборы значений функций составляют множество E2´Е2, поэтому количество функций одной переменной равно числу элементов прямого произведения E2 Функции двух переменных:
Некоторые из этих функций носят специальные названия и играют такую же роль, как элементарные функции в анализе, поэтому называются элементарными функциями алгебры логики. 1) f1(x1, x2) = (x1&x2) – конъюнкция х1 и х2 (логическое умножение). 2) f6(x1, x2) = (x1 3) f7(x1, x2) = (x1 4) f8(x1, x2) = (x1 5) f9(x1, x2) = (x1~x2) – х1 эквивалентно х2. 6) f13(x1, x2) =(x1 7) f14(x1, x2) = (x1|x2) – х1 штрих Шеффера х2 (отрицание конъюнкции). Cимволы Обозначим множество всех функций двузначной алгебры логики Р2. Обозначим через Р2(n) число функций, зависящих от n переменных. Очевидно, Равенство функций Определение. Переменная хi называется существенной переменной функции алгебры логики
В противном случае переменная xi называется фиктивной. Наборы, отличающиеся лишь одной переменной xi, называются соседними по xi. Пример.
Для функции Для функции Пусть Определение. Функции Принцип двойственности Определение. Функция Пример. Константа 0 двойственна к 1:
Определение. Если Если Пример3.Покажем, что
Теорема (о двойственных функциях). Если Теорема (о принципе двойственности). Если функция задана некоторой формулой, то, чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные, 0 на 1, 1 на 0. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (символ принадлежности). Пишут:
(символ принадлежности). Пишут:  и говорят, что элемент а принадлежит множеству А. В случае, когда а не является элементом множества А, пишут
и говорят, что элемент а принадлежит множеству А. В случае, когда а не является элементом множества А, пишут  . Множество может содержать как конечное, так и бесконечное число элементов, соответственно говорят, что множество конечно или бесконечно.
. Множество может содержать как конечное, так и бесконечное число элементов, соответственно говорят, что множество конечно или бесконечно. , если они состоят из одних и тех же элементов.
, если они состоят из одних и тех же элементов. Z
Z 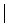 хÎА либо хÎВ}.
хÎА либо хÎВ}. хÎА и хÏВ}.
хÎА и хÏВ}.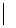 хÎА и хÎВ}.
хÎА и хÎВ}.

 .
.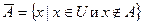 .
. и
и  из универсума U справедливы законы де Моргана:
из универсума U справедливы законы де Моргана: .
. ÎA и bÎ B}.
ÎA и bÎ B}. .
.
 .
. ,
,  ,
, 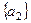 ,
,  ,
,  ,
,  ,
,  ,
, 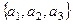 .●
.● .
. .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
. .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
.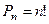 .
. ,
,  .
. множества
множества  ,
, .
. способами и после каждого из таких выборов объект
способами и после каждого из таких выборов объект  способами, то выбор «
способами, то выбор «  способами.
способами. способами.
способами. ;
;  – прямое произведение n сомножителей, т.е.
– прямое произведение n сомножителей, т.е.  .
.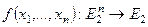 .
. конечно, то задать отображение
конечно, то задать отображение  означает задать множество наборов из
означает задать множество наборов из  .
. , тогда
, тогда  {
{  ,
,  ,
,  ,
,  }. Отображение
}. Отображение  ;
;  ,
,  ,
,  .
. , которую можно записать в виде таблицы:
, которую можно записать в виде таблицы: , называется таблицей истинности для этой функции.
, называется таблицей истинности для этой функции. – константа нуль
– константа нуль – тождественная функция
– тождественная функция – отрицание х
– отрицание х – константа единица
– константа единица E2, т.е. 4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции.
E2, т.е. 4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции. x2) – сложение х1 и х2 по модулю два.
x2) – сложение х1 и х2 по модулю два. x2) – х1 дизъюнкция х2 (логическое сложение).
x2) – х1 дизъюнкция х2 (логическое сложение). x2) – х1 стрелка Пирса х2 (отрицание дизъюнкции), другие названия: функция Вебба, функция Даггера.
x2) – х1 стрелка Пирса х2 (отрицание дизъюнкции), другие названия: функция Вебба, функция Даггера. x2) – х1 импликация х2.
x2) – х1 импликация х2. , &,
, &,  ,
,  .
. , если существуют такие значения
, если существуют такие значения  что
что
 .
.
 – фиктивная переменная, т.к.
– фиктивная переменная, т.к.  ,
,  , т.е. не существует наборов
, т.е. не существует наборов  и
и  таких, что
таких, что  .
.
 и
и  и
и  таких, что
таких, что  . Если
. Если 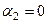 , то
, то  , если
, если  , то
, то  . Аналогично доказывается, что
. Аналогично доказывается, что  является фиктивной переменной для функции
является фиктивной переменной для функции  . Тогда ее можно удалить из таблицы истинности, вычеркнув все строки вида
. Тогда ее можно удалить из таблицы истинности, вычеркнув все строки вида  или, наоборот, все строки вида
или, наоборот, все строки вида 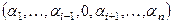 и столбец для переменной
и столбец для переменной  . Будем говорить, что функция
. Будем говорить, что функция 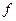 получена из
получена из  путем введения фиктивной переменной
путем введения фиктивной переменной  и
и  называются равными, если
называются равными, если  называется двойственной к функции
называется двойственной к функции 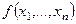 , если
, если  .
.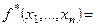
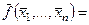
 – самодвойственная функция.
– самодвойственная функция. двойственна к
двойственна к