
|
|
Использование взаимно однозначного соответствия множеств
Пример. Найти количество всех подмножеств множества из N элементов.
Решение. Обозначим каждое подмножество набором нулей и единиц, всего из N элементов. При этом на позиции номер i стоит 1, если элемент номер i содержится в подмножестве, и 0, если не содержится в нём. Тогда различных наборов 2N, поскольку на каждом из N мест может находиться или 0, или 1. Количество подмножеств равно количеству наборов, поскольку подмножества и наборы нулей и единиц находятся во взаимно-однозначном соответствии. Итак, количество подмножеств равно 2N.
Ответ. 2N.
Принцип включений исключений
Рассмотрим задачу. Пример. Из 35 студентов 20 изучает английский язык, 15 – немецкий, 10 – французский, 7 – английский и немецкий, 5 – английский и французский, 4 – немецкий и французский, 3 – английский, французский и немецкий. Сколько студентов не изучает ни один из перечисленных языков?
Существует формула, называемая формулой включений-исключений, которая дает ответ на этот вопрос: N(0)=N-(N1+N2+N3)+(N12+N13+N23)-N123. Что она означает? N – общее число студентов. N1- число студентов, изучающих английский язык, N12 – английский и немецкий и т.д., N(0) – число студентов не изучающих ни один из перечисленных языков.
Для иллюстрации рассуждений такого типа используются рисунки, называемые диаграммами Венна. Например, множество всех студентов в группе обозначено прямоугольником. Множество А обозначает всех студентов, знающих немецкий язык, множество В – всех студентов, знающих английский язык. Множество АВ (в центре рисунка) обозначает множество студентов, знающих оба иностранных языка, заштрихованная часть рисунка – студентов, знающих хотя бы один иностранный язык. Наконец, не заштрихованная часть внутри прямоугольника – множество студентов группы, не знающих ни одного иностранного языка.
Пример. В группе из 25 человек 16 человек знает французский язык, 22 знают английский язык, один не знает ни одного иностранного языка. Сколько студентов знают хотя бы один из двух иностранных языков?
Задача: Секретарь рассыпал письма из конвертов, и обратно положил их наугад, по одному письму в конверт. Найти вероятность того, что хотя бы одно письмо попадёт не в свой конверт. Примечание: ответ практически не зависит от количества писем и приближённо равен 1 – 1/e, причём уже начиная с n = 6 совпадение с точностью до 4 знаков после запятой.
Бином Ньютона
(a + b)n = Для доказательства формулы можно рассмотреть выражение (a + b) ∙ (a + b) ∙… ∙ (a + b). Подсчитаем, сколько раз в этом выражении встретится bk. Это выражение встретится столько раз, сколько способов выбрать k скобок, из которых возьмём b, среди всех n скобок. А это количество способов равно Из оставшихся (n-k) скобок выберем (n-k) множителей a. Таким образом, получим слагаемое
Свойства биномиальных коэффициентов
Доказательство. Подставим в бином Ньютона a = b = 1.
Доказательство. Подставим в бином Ньютона a = 1, b = -1.
Шары и перегородки
Рассмотрим задачу: сколько способов представить число n в виде суммы k натуральных слагаемых? Можно представить её так: набор из n шаров, расположенных в ряд, разделить на k частей, поставив (k-1) перегородок. В таком виде задача гораздо понятнее, поскольку мы должны выбрать (k-1) мест из (n-1) возможных. А количество сделать это мы знаем -
Пример. Сколько способов представить 10 в виде суммы шести натуральных слагаемых? Решение. Представим формулировку в таком виде: разбить цепочку из 10 шаров на шесть групп. Для этого достаточно разместить пять перегородок в 9 промежутках. (НАРИСОВАТЬ!) Это можно сделать Ответ:
Можно усложнить задачу: сколько способов представить число n в виде суммы k целых слагаемых, каждое из которых не меньше m?
Эту задачу можно свести к предыдущей: для случая m = 1 решать задачу мы умеем, а для общего случая для xi ≥ m (при i = 1, 2, …, k) можно сделать замену yi = xi – m + 1. Получим задачу для чисел y1, y2, … yk, сумму которых мы можем вычислить: y1 + y2 + … + yk = (x1 – m + 1) + (x2 – m + 1) + … + (xk – m + 1) = (x1 + x2 + … + xk) + k(-m+1) = n – km + k. Таким образом, все числа yi натуральные, причём их сумма известна. Такую задачу мы решать уже умеем.
Пример. Сколько способов представить 100 в виде суммы шести натуральных слагаемых, каждое из которых не меньше 3? Если каждое из чисел не меньше 1 (то есть натуральное), то способов будет Если по условию все Итак, получили задачу: сколько способов представить число 88 в виде шести натуральных слагаемых? Такую задачу мы умеем решать. Ответ в данном случае будет равен
Пример. Сколько способов представить 100 в виде суммы шести натуральных слагаемых, каждое из которых не меньше -4? Если по условию все Сколько способов представить число 130 в виде шести натуральных слагаемых? Ответ:
Треугольник Паскаля
Рассмотрим задачу, сочетающую правило сложения и нахождение числа сочетаний. Вывести рекуррентную формулу для подсчета биномиальных коэффициентов. Выделим из n элементов один и разобьем все k-элементные подмножества на два класса: - содержащие выделенный элемент и - не содержащие его. Первых будет Вторых будет Так как любое подмножество (сочетание) принадлежит либо одному, либо другому классу и классы не пересекаются, получаем рекуррентную формулу:
Процесс вычислений по этому рекуррентному соотношению можно представить в виде пирамиды, которая называется треугольником Паскаля:
В этом треугольнике каждое число по выведенной рекуррентной формуле есть сумма двух, стоящих над ним, а по границам треугольника стоят единицы.
1 1 1 2 1 1 3 3 1 1 4 6 4 1 ……………….. Например, (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 .
. . Так сделаем для k от 0 до n.
. Так сделаем для k от 0 до n.
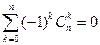
 .
.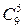 способами.
способами.
 (5 перегородок в 99 промежутков).
(5 перегородок в 99 промежутков). , можем сделать замену yi = xi – 2, тогда все
, можем сделать замену yi = xi – 2, тогда все  , то есть получили задачу для суммы натуральных чисел. При этом сумма всех yi будет на 12 меньше суммы всех xi, то есть будет равна 100 – 12 = 88.
, то есть получили задачу для суммы натуральных чисел. При этом сумма всех yi будет на 12 меньше суммы всех xi, то есть будет равна 100 – 12 = 88. .
. , можем сделать замену yi = xi + 5, тогда все
, можем сделать замену yi = xi + 5, тогда все  .
. , так как один элемент уже выбран, и из оставшихся n-1 элементов надо выбрать еще k-1 элемент.
, так как один элемент уже выбран, и из оставшихся n-1 элементов надо выбрать еще k-1 элемент. , так как один элемент запрещается выбирать, и надо выбрать все k элементов из оставшихся n-1.
, так как один элемент запрещается выбирать, и надо выбрать все k элементов из оставшихся n-1.
