
|
|
ГЛАВА 10. НЕСОБСТВЕННЫЕ (ОБОБЩЕННЫЕ) ИНТЕГРАЛЫ12 (Интегрирование на некомпактном промежутке) Ранее был рассмотрен определенный интеграл, необходимым условием существования которого являлось условие ограниченности подынтегральной функции на отрезке df.1 Компактным промежутком будем называть df.2 Пусть df.3 Пусть f(x) – определена на промежутке
называют несобственным интегралом от функции f(x) на промежутке Очевидно возможны 2 частных случая: 1) Интеграл с бесконечным верхним пределом:
2) Интеграл от неограниченной функции:
Заметим, что если
df.4 Пусть f(z) определена на промежутке
называется несобственным интегралом от функции f(x) на Опять возможны два случая: 1) с бесконечным нижним пределом:
2) интеграл от неограниченной функции:
df.5 Пусть f(x) определена df: ЗАМЕЧАНИЕ. Можно показать, что в этом определении значение н. и. не зависит от выбора (.) ”c”. Заметим также, что последнее определение эквивалентно следующему определению:
т.е. здесь рассматривается предел функции двух переменных ”y”
По определению полагаем геометрический смысл н. и. – площадь соответствующих «бесконечных» криволинейных трапеций.
f(x) f(x) ченная вU(в) 0 a x 0 a
y y
f(x) f(x) ченная в U(a) 0 в x 0 a’ a в x
df.5 df.5 f(x) ниченная в U(а) 0 x a 0 в x
Если соответствующие пределы в определениях 3, 4 Можно показать, что свойства интегралов из df. 3 Поэтому в дальнейшем изложении в основном ограничимся несобственными интегралами типа (1), т.е. df. 3
Многие из них (однако, не все) аналогичны свойствам определенного интеграла.
Пусть f(x)
При этом под F(в) понимается:
Доказательство: Т. к.
2 Пусть
Доказательство: Из сходимости
Переходим в последнем равенстве к пределу при
3 Пусть
4 Пусть: 1. 2. Пара из трех функций
При этом входящие в (1)выражения понимаются в несобственном смысле. (Свойства 3 и 4 доказать самостоятельно).
5 Пусть: 1. 2. 3. Тогда Отметим, что, используя свойство 5, можно показать, что всегда от интеграла с бесконечным пределом можно перейти к интегралу от неограниченной функции и наоборот. Пусть, например,
при x=a, t=0; при x=в-0, t=
Поэтому далее в основном будем рассматривать интегралы вида:
6 (от латинского additivus – прибавляемый, свойство величин). Пусть Доказательство: Пусть =(предел слева
§ 10.3 ПРИЗНАКИ СХОДИМОСТИ Н. И. Будем рассматривать интегралы вида:
Th.1 1) 2) Причем условия 1 и 2 эквивалентны. Доказательство: Условие 1 следует из определения
Переходя к пределу при Следствие. Очевидно, что Следовательно, простейшим способом установления сходимости несобственного интеграла является вычисление его по формуле Ньютона – Лейбница:
Однако, не всегда возможно найти В этом случае используются признаки сходимости, о которых будет идти речь ниже.
Th.2Критерий Коши.
Доказательство: В силу Th.1 (Необходимо полагать Но ●Достаточно эффективных при практическом использовании признаков (теорем) сходимости н.и. от произвольных функций не существует. Поэтому далее ограничимся только случаем неотрицательных функций, т.е. Отметим при это, что Т.о. все результаты, полученные для неотрицательных функций могут быть перенесены на неположительные функции (
Th.3 Необходимое и достаточное условия сходимости для Неотрицательных функций. Пусть частичный интеграл Доказательство: Покажем, что Но из I семестра известно: Пусть Дополнительно получим:
Но по Th.1
Рассмотрим два интеграла: 1)
Th.4 Признак сравнения. Пусть: a) б) Тогда: а) из сходимости (2) б)из расходимости (1) Доказательство:
Пусть Т.о. Аналогично: (1)расходится на Следствие. Th.4 окажется в силе, если условие б) выполняется
Th.5 Признак сравнения в предельной форме. Пусть: а) б) в) Тогда: Интеграл (2)сходится Интеграл (1)расходится Доказательство: Т.к.
Обозначив Следствие 1. При условиях Th.5 а) и б), и замене в) на Доказательство: Для доказательства достаточно учесть, что т.к. по Th.5: сходимость (1) Итак, сходится (1) Следствие 2. Если
Замечание. Аналогичные признаки сравнения можно сформулировать для других типов Н. И.
Нужно только в Th.4 потребовать выполнение неравенства на соответствующем интервале В Th.5 предел при

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . При этом подразумевалось, что отрезок интегрирования
. При этом подразумевалось, что отрезок интегрирования  -ой сегмент
-ой сегмент  .
. - полуинтервал числовой прямой
- полуинтервал числовой прямой  , причем ” в ” может быть
, причем ” в ” может быть  , символами
, символами  , а функция
, а функция  интегрируема на
интегрируема на  .
. и f(x)
и f(x) 
 , тогда предел
, тогда предел (1)
(1) и конечен.
и конечен. ,
,  .
. , в=const в этом случае
, в=const в этом случае 

 (ограничена), тогда получаем обычный интеграл Римана. В силу непрерывности функции
(ограничена), тогда получаем обычный интеграл Римана. В силу непрерывности функции  на
на  ), т.е.
), т.е.
 . (
. (  ) и
) и  . Тогда предел
. Тогда предел (2)
(2) , если предел
, если предел 
 .
.
 , что
, что  , то по df:
, то по df:  .
. df:
df: ”z”. Т.е. при вычислении предела
”z”. Т.е. при вычислении предела  стремятся к
стремятся к  независимо.
независимо.
 и н.и.
и н.и.  -ет (i=1,2,..., n). Тогда н. и. от f(x) на
-ет (i=1,2,..., n). Тогда н. и. от f(x) на  df:
df: y df.3 y df.3
y df.3 y df.3
 в x
в x
 f(x) – неограни-
f(x) – неограни- y y
y y  f(x) f(x) неогра-
f(x) f(x) неогра- и т.д.), а интеграл – сходится. В противном случае интеграл – расходится.
и т.д.), а интеграл – сходится. В противном случае интеграл – расходится. . Формула Ньютона – Лейбница.
. Формула Ньютона – Лейбница. и F(x)- первообразная f(x) на
и F(x)- первообразная f(x) на 


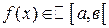 , то
, то  по формуле Ньютона – Лейбница на
по формуле Ньютона – Лейбница на  :
:

 . Линейность.
. Линейность. :
:  и
и (1)
(1)
 :
: 
 .
. или
или  , т.к.
, т.к.  равенство (1).
равенство (1). и
и  , тогда
, тогда  .
.
 интегрируема на
интегрируема на  -
-  (1)
(1) .
. ,
,  .
. , причем оба интеграла сходятся или расходятся одновременно. (Без доказательства).
, причем оба интеграла сходятся или расходятся одновременно. (Без доказательства). . Сделаем замену
. Сделаем замену  ;
;

 , тогда
, тогда  .
. , тогда
, тогда  и
и  .
. :
: 
 предел справа) =
предел справа) =  .
. и назовем его частным интегралом, а
и назовем его частным интегралом, а  - остатком.
- остатком.
 и конечен.
и конечен. .
. . В силу аддитивности:
. В силу аддитивности: .
. получим
получим  , т.о.
, т.о.  , что также
, что также 
 или нахождение ее громоздко.
или нахождение ее громоздко.
 .
. , но по критерию Коши существования конечного предела
, но по критерию Коши существования конечного предела  (смотри I семестр):
(смотри I семестр):  :
:  .
. , т.к.
, т.к.  ).
). .
. .
. по свойству линейности.
по свойству линейности. ) с небольшими изменениями.
) с небольшими изменениями. Тогда
Тогда 
 .
. на
на  -монотонно возрастает). Действительно, пусть
-монотонно возрастает). Действительно, пусть  . Очевидно,
. Очевидно,  , т.к.
, т.к.  .
. - ограничена на
- ограничена на 


 (2)
(2) .
. .
. Пусть (2)сходится
Пусть (2)сходится  - ограничена на
- ограничена на  :
:  .
. - неограниченна
- неограниченна  , т.е
, т.е  ,
,  или
или  . Действительно,
. Действительно, , 1-ое слагаемое постоянно и не влияет на сходимость.
, 1-ое слагаемое постоянно и не влияет на сходимость. .
. .
. или
или ,т.к g(x)
,т.к g(x) 
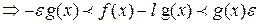
 - рассмотрим это неравенство.
- рассмотрим это неравенство. , т.к
, т.к  , т.о.
, т.о.  , т.к.
, т.к.  по Th.4
по Th.4  (1)и (2)сходятся иди расходятся одновременно.
(1)и (2)сходятся иди расходятся одновременно.

 сходится (2),расходится (2)
сходится (2),расходится (2)  (эквивалентны) при
(эквивалентны) при  , то (1) и (2)сходятся или расходятся одновременно. Это частный случай следствия 1, т.е при l=1.
, то (1) и (2)сходятся или расходятся одновременно. Это частный случай следствия 1, т.е при l=1.
 .
. или
или  .
.