|
|
Расчет всасывающего трубопроводаРассмотрим схему работы насоса, включенного в систему, подающую жидкость из резервуара А в напорный резервуар В (рисунок 1.1)
Жидкости, проходящей через насос, сообщается энергия, которая расходуется на подъем ее в напорный резервуар, и на преодоление сопротивлений в напорном трубопроводе. Вертикальное расстояние hH от центра насоса до уровня жидкости в напорном резервуаре называется геометрической высотой нагнетания. Вертикальное расстояние от уровня жидкости в приемном резервуаре до центра рабочего колеса насоса называется геометрической высотой всасывания hBC. Полный напор насоса Н определяется как разность напоров, создаваемых потоком в сечениях, соответствующих началу нагнетательного трубопровода Н2 и концу всасывающего трубопровода Нь т.е. H=H2-Hi. В этих сечениях обычно устанавливают манометры и вакуумметры. Составив уравнение Д.Бернулли для двух сечений 1-1 и 2-2 и выполнив некоторые преобразования, получим:
Расчет простого трубопровода Трубопроводы, состоящие из одной линии труб и имеющие один и также расход жидкости, называется простым. В зависимости от соотношения местных потерь напора и потерь по длине различают короткие и длинные трубопроводы. К коротким относят трубопроводы малой длины с большим числом местных сопротивлений (местные потери напора соизмеримы с потерями напора по длине), а к длинным - трубопроводы, в которых местные потери напора пренебрежимо малы по сравнению с потерями напора по длине (менее 5%). Примерами коротких трубопроводов могут служить всасывающие трубы насосов, дюкеры, сифоны и.д.; длинные - водопроводы, нефтепроводы, газопроводы и т.д. Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубы больше, чем в конце. Этот запас энергии обеспечивается тем или иным способом: работой насоса, созданием разностей уровней жидкости, давлением газа и.т.д. 2.1 Пример расчета простого длинного трубопровода Для длинного трубопровода постоянного по всей длине диаметра (рис.2Л) составляется уравнение Д.Бернулли для сечений 1-1 и 2-2.
После ряда преобразований получена зависимость для определения располагаемого напора Н:
где: А – удельное сопротивление трубопровода, с /м , определяемое по таблице 2.1 и имеющее выражение:
L – длина трубопровода, м; Q - расход жидкости, м2/с. Таблица 7 – Значение А для труб, бывших в эксплуатации (при скорости V>1,2 м/с)
Продолжение талицы 7
При гидравлическом расчете простого трубопровода обычно известны его длина I, материал и конфигурация. Неизвестной может быть одна из трех величин: Н, Q или d. Для практического применения используют соотношение:
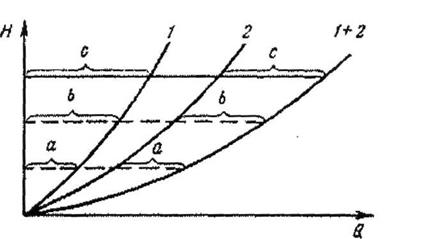
В случае последовательного соединения участков трубопровода предварительно строят характеристики отдельных участков, например 1 и 2 (рис. 3.2). Чтобы построить характеристику всего трубопровода, следует сложить потери напора при одинаковых расходах, т.е. сложить ординаты кривых 1 и 2 при равных абсциссах.
При параллельном соединении также прежде всего следует построитель характеристики отдельных параллельных участков. Пусть кривые 1 и 2 (рис. 3.3) представляют собой такие характеристики двух параллельных участков. Так как при параллельном соединении общий расход определяется как сумма расходов на отдельных участках, а потери напора на них одинаковы, то для построения
а, б, с – расходы на участке 1 Рисунок 3.3 – Построение характеристики трубопровода с параллельным соединением участков где: А0=А к™ Кп – поправочный коэффициент, учитывающий зависимость коэффициента гидравлического трения X от числа Рейнольдса и определяется по Таблице 8 Таблица 8 – Значение коэффициента Кп 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

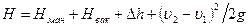 , (22)
, (22)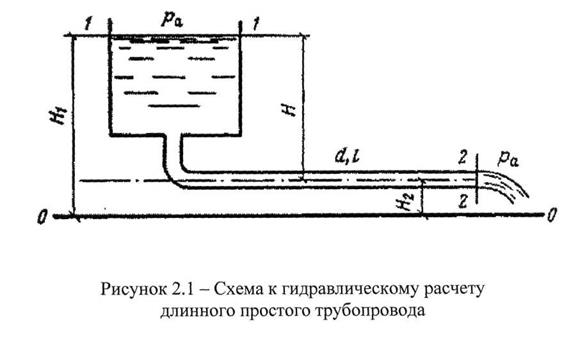
 , (23)
, (23) , (24)
, (24) , (25)
, (25)