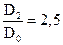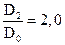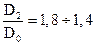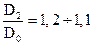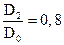|
|
Характеристики центробежных насосовЧасть II. Гидравлические машины Глава 11. Общие сведения о гидромашинах Классификация гидравлических машин
Гидравлические машины – это машины, предназначенные для преобразования механической энергии в гидравлическую (насосы), гидравлической энергии в механическую (гидродвигатели) и для передачи механической энергии от одного вала к другому с помощью жидкости (гидропередачи).
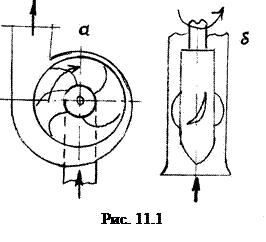
К группе лопастных насосов относят центробежные и пропеллерные насосы В центробежных насосах под воздействием центробежной силы при вращении колеса с лопатками частицы жидкости отбрасываются от центра к периферии. Благодаря этому жидкость засасывается через центральное отверстие и выбрасывается в корпус, а затем в нагнетательный патрубок. За счет работы центробежных сил происходит увеличение энергии жидкости и следовательно создается тот или иной напор. В пропеллерных или осевых насосах лопасти образуют как бы часть винтовой поверхности, поэтому при вращении они ввинчиваются в жидкость и заставляют ее перемещаться в осевом направлении.
В объемных насосах подача жидкости и повышение давления происходит за счет вытеснения ее из рабочего объема теми или иными вытеснителями (рис. 11.4 а, б, в). В поршневом насосе (рис. 11.4 а) вытеснение жидкости производится поршнем, совершающим возвратно-поступательное движение в цилиндре. В пластинчатом насосе (рис. 11.4 б) вытеснение жидкости производится пластинами, а в шестеренном насосе жидкость выдавливается из впадины зубом.
Наконец, объемная гидропередача, также как и лопастная состоит из насоса н и гидродвигателя д, но эти машины работают по объемному принципу (рис.11.6). Кроме указанных выше гидравлических машин существуют бесприводные насосы, в которых отсутствуют вращающиеся и перемещающиеся одна относительно другой детали. Перемещение жидкости в таких насосах осуществляется за счет использования различных эффектов (см. гл.12.17).
Глава 12. Насосы 12.1. Общие сведения о насосах. Устройство насосной установки.
Насосами называются гидравлические машины, предназначенные для подъема, нагнетания и перемещения жидкости. Рассмотрим устройство насосной установки (рис. 12.1). Она состоит из следующих элементов: 1. насос; 2. всасывающий трубопровод; 3. фильтр с обратным клапаном; 4. задвижка; 5. нагнетательный трубопровод; 6. емкость для жидкости; 7. манометр; 8. вакуумметр. Работу насоса характеризуют следующие параметры: 1. Напор H, м.ст.жидкости 2. Производительность Q, м3/с; 3. Мощность N, кВт; 4. Коэффициент полезного действия h; 5. Высота всасывания hвс, м; 6. Число оборотов n, об/мин. Напором насоса называется приращение удельной энергии, сообщаемое насосом нагнетаемой жидкости.
где
1. насос; 2. всасывающий трубопровод; 3. фильтр с обратным клапаном; 4. задвижка; 5. нагнетательный трубопровод; 6. емкость для жидкости; 7. манометр; 8. вакуумметр.
Рис. 12.1
Полную удельную энергию жидкости на входе получим из уравнения Бернулли, составленного для сечений 0-0 и 1-1
Отсюда
Полную удельную энергию жидкости
Здесь скорости в сечениях 0-0 и 3-3 приняты равными нулю, hw вс и hw н – потери напора во всасывающей и нагнетательной трубах. Имея в виду (12.3) и (12.4), получим
Напор, развиваемый насосом, расходуется на преодоление разности давлений в объемах всасывания и нагнетания, на подъем жидкости на геометрическую высоту hг и на преодоление сопротивлений во всасывающем и нагнетательном трубопроводах. Напор, создаваемый насосом, можно представить в следующем виде
где hд – динамический напор, hст – статический напор. Можно выразить напор по показаниям приборов
Знак плюс или минус подставляется в формулу в зависимости от того, где установлен манометр. Производительность насоса зависит от его конструкции и, рассматривая ниже конкретные насосы, о производительности будем говорить особо. Мощность насоса можно определить из следующих соображений: каждой единице веса жидкости насос передает энергию в количестве Нм, за единицу времени через насос протекает жидкость весом rgQ. Следовательно, энергия, передаваемая насосом жидкости за единицу времени, или полезная мощность
Мощность, подведенная к валу насоса N естественно больше полезной мощности на величину потерь в насосе. Эти потери мощности оцениваются коэффициентом полезного действия насоса h
Рассмотрим баланс энергии в насосе (рис.12.2). Здесь введены обозначения: N – мощность на валу; Nт – теоретическая мощность; Nм – мощность механических потерь; Nо – мощность объемных потерь; Nг – мощность гидравлических потерь. Механические потери – это потери на трение в подшипниках, сальниках, на трение поршня о стенки цилиндра, на трение наружной поверхности колес о жидкость. Оцениваются механические потери механическим КПД
Объемные потери – это потери на утечки жидкости. В разных насосах они имеют разный характер и констатируют тот факт, что теоретическая подача больше, чем действительная. Оцениваются эти потери объемным КПД
Гидравлические потери – это потери на преодоление гидравлических сопротивлений в элементах насоса. Они оцениваются гидравлическим КПД
В формулах (12.11), (12.12) Q, H – соответственно действительные напор и производительность, а Qт, Hт – их теоретические значения. Заметим, что в (12.10) N – Nм – это теоретическая мощность
Запишем
Умножим числитель и знаменатель (12.14) на произведение Q, H
Учитывая (12.9), (12.11), (12.12) получим
или
Таким образом коэффициент полезного действия насоса равен произведению всех частных КПД. При проектировании и создании насосной установки необходимо знать наибольшую высоту, на которой может быть установлен насос или, так называемую высоту всасывания. Высота всасывания определяется величиной допустимого разрежения при входе в насос. Для определения высоты всасывания составим уравнение Бернулли для сечений 0-0 и 1-1 (рис.12.1)
Отсюда разрежение на всасывании, выраженное в виде вакуумметрической высоты Нv, будет
Это уравнение показывает, что вакуумметрическая высота больше, чем высота всасывания на величину суммы скоростного напора и потерь напора на преодоление сопротивлений. При работе центробежных, ротационных, шестеренных насосов жидкость во всасывающем трубопроводе движется равномерно и, следовательно, потери напора складываются из потерь по длине и в местных сопротивлениях. У поршневых насосов в силу неравномерного, ускоренного движения поршня, а следовательно и ускоренного движения жидкости во всасывающей трубе, в потерях напора следует учитывать, так называемый инерционный напор. Из (12.19) получим
Из (12.20) видно, что с увеличением высоты всасывания должно снижаться давление р1. Минимальным значением, до которого может понизиться р1, является давление парообразования рп и максимальная высота всасывания будет
При понижении давления во всасывающей трубе ниже давления парообразования возникает вскипание жидкости. Пузырьки пара уносятся в область повышенного давления, где происходит его конденсация. При этом образуются пустоты, которые мгновенно захлопываются и возникают местные гидравлические удары. Под воздействием этих ударов происходит разрушение металла. Явление, описанное выше, носит название кавитация. Кавитация сопровождается характерным шумом, вибрацией и, если область парообразования оказывается достаточно большой, приводит к срыву работы, т.е. к резкому снижению подачи, напора и КПД. Для того, чтобы избежать кавитации высота всасывания уменьшается на некоторую величину Dh, обеспечивающую минимальный кавитационный запас
Величина Dh может быть рассчитана по формуле Руднева
где ск – коэффициент, зависящий от конструкции и быстроходности насоса. Интерес представляет определение теоретической предельной высоты всасывания. Так для воды, полагая, что р1 = 0; v1 » 0; hw вс = 0 получим
12.2. Основы теории лопастных насосов. Устройство и принцип Принципиальная схема центробежного насоса изображена на рис.12.3
Выведем основное уравнение центробежных машин. Для этого рассмотрим упрощенную схему: предположим, что колесо имеет бесконечное множество бесконечно тонких лопаток. Это позволяет считать, что между соседними лопатками жидкость протекает в виде элементарной струйки. Кроме того будем полагать, что жидкость является идеальной. Частицы жидкости совершают в колесе сложное движение – они вращаются вместе с колесом и под воздействием центробежной силы движутся вдоль каналов к периферии. Изобразим треугольники скоростей на входе и выходе из колеса насоса (рис. 12.4). Здесь буквой u обозначена окружная скорость, w – относительная скорость, c – абсолютная скорость.
 Воспользуемся теоремой о моменте количества движения, которая гласит: сумма изменений моментов количества движения жидкости относительно оси вращения колеса в единицу времени равна сумме моментов внешних сил Воспользуемся теоремой о моменте количества движения, которая гласит: сумма изменений моментов количества движения жидкости относительно оси вращения колеса в единицу времени равна сумме моментов внешних сил
Изменение момента количества движения для элементарной струйки
где dM1 и dМ2 – моменты количества движения в единицу времени во входном и выходном сечениях элементарной струйки. Для любого сечения
Изменение момента количества движения вдоль элементарной струйки
Просуммируем изменение моментов количества движения
Теоретическая мощность в соответствии с (12.8)
где Нт – теоретический напор; Qт – теоретическая производительность. С другой стороны, выразив теоретическую мощность через угловую скорость колеса w, запишем
Тогда
после подстановки (12.29) и u=wr теоретический напор
Полученное уравнение называется уравнением Эйлера для центробежных машин (1754 г.). Проанализируем уравнение Эйлера. Из (12.33) видим, что максимальное значение теоретический напор будет иметь место в том случае, когда второй член в числителе обратится в нуль. Это возможно осуществить за счет угла α1. Когда α1 = 90° cos α1 = 0 и
 Выходные концы лопаток могут быть направлены по-разному и образовывать различные углы β2. Этот угол называется углом профиля. В зависимости от величины β2 различают три формы лопастей: загнутые назад β2 < 90°, радиальные β2 = 90°, загнутые вперед β2 > 90° (рис. 12.5). Обращаясь к формуле (12.34) и рис. 12.5 видим, что с увеличением угла β2 угол a2 уменьшается, следовательно увеличивается cos a2 и одновременно возрастает и скорость с2. Однако это еще не означает, что насос с большим углом β2 развивает наибольший напор. Оценим, какая доля всей энергии передается жидкости в виде энергии давления. Эта доля оценивается коэффициентом реактивности, который выражает отношение статического напора Нст к полному Н=Нд+Нст и обозначается буквой ρ Выходные концы лопаток могут быть направлены по-разному и образовывать различные углы β2. Этот угол называется углом профиля. В зависимости от величины β2 различают три формы лопастей: загнутые назад β2 < 90°, радиальные β2 = 90°, загнутые вперед β2 > 90° (рис. 12.5). Обращаясь к формуле (12.34) и рис. 12.5 видим, что с увеличением угла β2 угол a2 уменьшается, следовательно увеличивается cos a2 и одновременно возрастает и скорость с2. Однако это еще не означает, что насос с большим углом β2 развивает наибольший напор. Оценим, какая доля всей энергии передается жидкости в виде энергии давления. Эта доля оценивается коэффициентом реактивности, который выражает отношение статического напора Нст к полному Н=Нд+Нст и обозначается буквой ρ
Отсюда следует, что коэффициент реактивности тем меньше, чем больше динамическая составляющая напора и выходная скорость с2. Как показывает опыт у колес с β2 < 90° ρ > 0,5; β2 = 90° ρ = 0,5; β2 > 90° ρ < 0,5. По этой причине колеса центробежных насосов делают с углами β2 = 20¸35°; β1 = 20¸30°. Уравнение Эйлера получено исходя из ряда упрощений (см. выше). Для того, чтобы учесть конечное число лопаток колеса и их конечную толщину вводится коэффициент sz, называемый поправкой на конечное число лопастей. Эта поправка может быть рассчитана по формуле Г. Ф. Проскура
где y = (0,55 ¸ 0,65) + 0,6 Sinb2, число лопастей z = 6 ¸12, отношение диаметров И наконец гидравлические потери, возникающие в насосе при движении в нем жидкости учитываются гидравлическим КПД hг. Тогда действительный напор
Характеристики центробежных насосов
Характеристиками насоса называются кривые, выражающие зависимости Н = f1(Q); N = f2(Q); h= f3(Q) при постоянном числе оборотов. Получим теоретическую характеристику Hт = f(Q) для чего в правую часть (12.34) введем производительность Qт. Для этого построим треугольник скоростей на выходе из колеса насоса (рис. 12.6).
где с2r – радиальная составляющая скорости
а b2 – ширина колеса насоса на выходе. Имя ввиду (12.38) и (12.39) получим
Обозначим
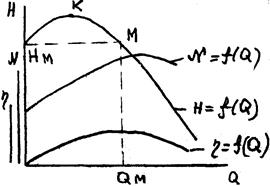
Действительная характеристика насоса отличается от теоретической, т.к. уравнение Эйлера, как указывалось выше, не учитывает конечное число лопастей, их конечную толщину и гидравлические потери в насосе. Теоретически учесть эти факторы пока не удается, поэтому рабочие характеристики получают испытаниями насоса на специальном стенде. Примерный вид характеристик представлен на рис. 12.8. Кривая H = f(Q) называется главной характеристикой. Иногда она имеет максимум в точке К. Левый участок ветви не пригоден для работы, т.к. здесь имеет место неустойчивая зона. Точка М главной характеристики соответствует максимальному КПД, а напор Нм и производительность Qм называются оптимальными.
12.4. Основы теории подобия лопастных насосов.
В связи со сложностью процессов движения жидкости в лопастных насосах не удается теоретически достаточно точно рассчитать характеристики. Поэтому приходится ориентироваться на имеющиеся образцы, лабораторные испытания моделей насосов и, базируясь на их характеристиках, путем пересчета получать характеристики вновь создаваемого насоса. Способы пересчета характеристик дает теория подобия, применительно к лопастным насосам. Эта теория позволяет получить формулы пересчета, определяющие зависимости подачи, напора и мощности геометрически подобных насосов, работающих на подобных режимах, от их размеров и числа оборотов. Напомним, что теория подобия требует соблюдения геометрического, кинематического и динамического подобия. 1. Геометрическое подобие требует подобия сходственных размеров и равенства углов. Так для насосов а и в одной серии (или натурного насоса и его модели)
где сl – константа геометрического подобия. 2. Кинематическое подобие требует подобия скоростей
3. Динамическое подобие потоков требует равенства критериев Ne, Re, Fr, Eu. Пользуясь указанными выше соотношениями, получим следующие зависимости. Отношение подач подобных насосов
Отношение напоров подобных насосов
Отношение мощностей подобных насосов
Здесь n – частота вращения, F – площадь выходного сечения рабочего колеса. Если один и тот же насос работает на разных числах оборотов, то сl = 1 и
Эти соотношения выражают законы пропорциональности центробежных насосов. Указанные законы являются приближенными, так как при изменении оборотов меняется и КПД насоса. В настоящее время широко применяется проектирование нового насоса путем пересчета по формулам подобия размеров существующего насоса. Для того, чтобы воспользоваться этим методом, необходимо выбрать из существующих насосов прототип, обладающий наилучшими показателями. Для выбора такого насоса необходим критерий подобия единый для всех типов насосов. Для подобных насосов, как указывалась выше
Запишем эти уравнения следующим образом
Величины q и h одинаковы для подобных насосов и являются критериями подобия, но они имеют существенный недостаток, так как содержат в своем составе линейный размер l, который заранее неизвестен. исключим из (12.49) и (12.50) l, возведя (12.49) в квадрат, а (12.50) в куб и разделим q2 на h3
или
Так как q и h постоянны для серии подобных насосов, то и nу тоже для нее одинаков и является искомым критерием подобия. Параметр nу называется удельным числом оборотов. Большее распространение имеет параметр
Этот параметр называется коэффициентом быстроходности. Если насосы подобны, то коэффициенты быстроходности у них одинаковы. В зависимости от величины коэффициента ns насосы делятся на: 1. Центробежные 1.1. Тихоходные ns = 40 ¸ 80; 1.2. Нормальные ns = 80 ¸ 150; 1.3. Быстроходные ns = 150 ¸ 300; 2. Диагональные ns = 300 ¸ 600; 3. Пропеллерные ns = 600 ¸ 1200;

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 По принципу действия гидравлические машины делятся на лопастные и объемные.
По принципу действия гидравлические машины делятся на лопастные и объемные.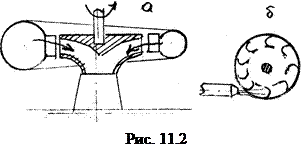 Примером лопастных гидродвигателей является гидравлическая турбина. Здесь жидкость под напором направляется на лопатки рабочего колеса и заставляет колесо вращаться. В реактивных турбинах жидкость проходя через криволинейные каналы, образованные лопатками, оказывает на них реактивное воздействие. В результате чего образуется крутящий момент, приводящий колесо во вращение (рис. 11.2 а). В активных турбинах струя жидкости, вытесненная под напором через сопло, оказывает на лопатки активное давление. За счет активной силы, действующей на лопатку, также образуется крутящий момент, приводящий колесо турбины во вращение (рис. 11.2 б).
Примером лопастных гидродвигателей является гидравлическая турбина. Здесь жидкость под напором направляется на лопатки рабочего колеса и заставляет колесо вращаться. В реактивных турбинах жидкость проходя через криволинейные каналы, образованные лопатками, оказывает на них реактивное воздействие. В результате чего образуется крутящий момент, приводящий колесо во вращение (рис. 11.2 а). В активных турбинах струя жидкости, вытесненная под напором через сопло, оказывает на лопатки активное давление. За счет активной силы, действующей на лопатку, также образуется крутящий момент, приводящий колесо турбины во вращение (рис. 11.2 б). Наконец примером лопастной гидропередачи является гидродинамическая муфта. Она представляет собой агрегат, состоящей из двух предельно сближенных колес: насосного и турбинного (рис. 11.3). При вращении насосного колеса от постороннего источника энергии в нем происходит преобразование механической энергии в гидравлическую. Жидкость под напором из насосного колеса поступает в турбинное, где происходит обратное преобразование гидравлической энергии в механическую. Таким образом связь между ведущим и ведомым валами осуществляется с помощью жидкости.
Наконец примером лопастной гидропередачи является гидродинамическая муфта. Она представляет собой агрегат, состоящей из двух предельно сближенных колес: насосного и турбинного (рис. 11.3). При вращении насосного колеса от постороннего источника энергии в нем происходит преобразование механической энергии в гидравлическую. Жидкость под напором из насосного колеса поступает в турбинное, где происходит обратное преобразование гидравлической энергии в механическую. Таким образом связь между ведущим и ведомым валами осуществляется с помощью жидкости. Примером объемного гидродвигателя является силовой цилиндр (рис. 11.5). Если в цилиндр подать жидкость под давлением она будет оказывать воздействие на поршень и, как следствие, на штоке будет действовать сила. Таким образом гидравлическая энергия преобразуется в механическую. Аналогично действуют объемные гидродвигатели вращательного действия.
Примером объемного гидродвигателя является силовой цилиндр (рис. 11.5). Если в цилиндр подать жидкость под давлением она будет оказывать воздействие на поршень и, как следствие, на штоке будет действовать сила. Таким образом гидравлическая энергия преобразуется в механическую. Аналогично действуют объемные гидродвигатели вращательного действия.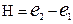 ,
,
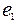 – полная удельная энергия жидкости перед насосом;
– полная удельная энергия жидкости перед насосом;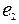 – полная удельная энергия жидкости после насоса.
– полная удельная энергия жидкости после насоса.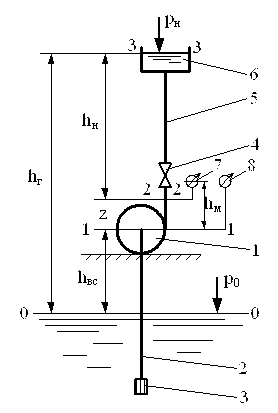
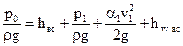 .
.
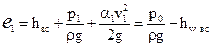 .
.
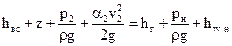 .
.
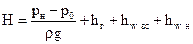 .
.
 ,
,
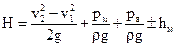 ,
,
 .
.
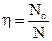 ,
,
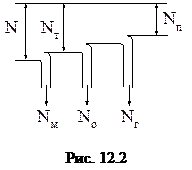 Потери мощности в насосе имеют разную физическую природу и делятся на механические, объемные и гидравлические.
Потери мощности в насосе имеют разную физическую природу и делятся на механические, объемные и гидравлические. .
.
 .
.
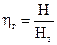 .
.
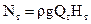 .
.
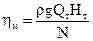 .
.
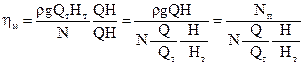 .
.
 ,
,
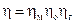 .
.
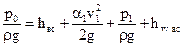 .
.
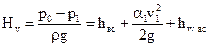 .
.
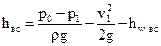 .
.
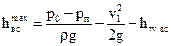 .
.
 .
.
 ,
,
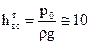 м.
м.
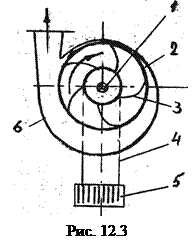 Простейший насос состоит из рабочего колеса 2, посаженного на вал 1, колесо имеет лопатки 3, изогнутые определенным образом. Рабочее колесо помещено в спиральный корпус с отводом 6. Жидкость в насос поступает в центральную часть колеса и под воздействием центробежных сил отбрасывается на периферию. За счет работы центробежных сил увеличивается напор жидкости. Цифрами 4 и 5 обозначены всасывающая труба и фильтр с обратным клапаном.
Простейший насос состоит из рабочего колеса 2, посаженного на вал 1, колесо имеет лопатки 3, изогнутые определенным образом. Рабочее колесо помещено в спиральный корпус с отводом 6. Жидкость в насос поступает в центральную часть колеса и под воздействием центробежных сил отбрасывается на периферию. За счет работы центробежных сил увеличивается напор жидкости. Цифрами 4 и 5 обозначены всасывающая труба и фильтр с обратным клапаном. .
.
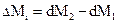 ,
,
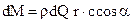 .
.
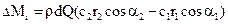 .
.
 .
.
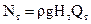 .
.
 .
.
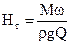 ,
,
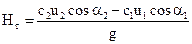 .
.
 .
.
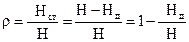 .
.
 ,
,
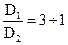 .
. .
.
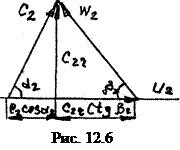 Из рис. 12.6 видно, что
Из рис. 12.6 видно, что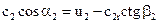 ,
,
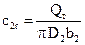 ,
,
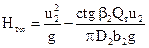 .
.
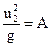 и
и 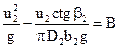 , тогда
, тогда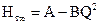 .
.
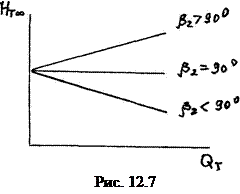 Таким образом получено уравнение характеристики, которое представлено на графике рис. 12.7. Зависимость
Таким образом получено уравнение характеристики, которое представлено на графике рис. 12.7. Зависимость  от Qт линейная и угол наклона характеристики к оси зависит от угла b2.
от Qт линейная и угол наклона характеристики к оси зависит от угла b2.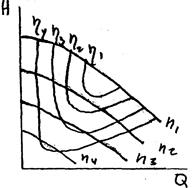
 При испытании насоса на разных числах оборотов получают универсальную характеристику. На ней наносят кривые напора при разных числах оборотов и кривые равных КПД (рис. 12.9)
При испытании насоса на разных числах оборотов получают универсальную характеристику. На ней наносят кривые напора при разных числах оборотов и кривые равных КПД (рис. 12.9)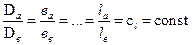 ,
,
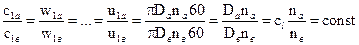 ,
,
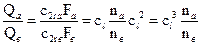 ,
,
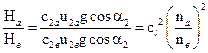 ,
,
 ,
,
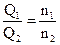 ;
; 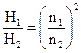 ;
; 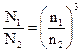 .
.
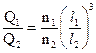 и
и  .
.
 ,
,
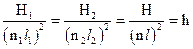 .
.
 ,
,
 .
.
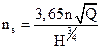 .
.