
|
|
ЦИРКУЛЯЦИЯ СКОРОСТИ. ВИХРЬ ВЕКТОРА СКОРОСТИЕсли в поле
называется циркуляцией скорости,а вектор, определяемый в виде
называется вихрем или ротором скорости. В данном случае В декартовой системе координат вихрь скорости вычисляется по формуле
На основании теоремы Стокса имеет место равенство
Проводя аналогию с механикой твердого недеформируемого можно отметить, что при движении элементарного объема жидкости можно выделить два вида движения, которые уже изучались в курсе теоретической механики - поступательное движение твердого тела со скоростью полюса и вращение его вокруг полюса. Для жидкости дополнительным видом движения является деформационное. Поэтому иногда подразделяют движение элементарного объема жидкости на квазитвёрдое(поступательное и вращательное) и деформационное. Из шести составляющих тензора, описывающего вращение жидкого объема вокруг полюса, только три отличаются друг от друга абсолютной величиной. Каждая из них определяет значение мгновенной угловой скорости вращения вокруг оси, параллельной одной из координатных осей. Эти угловые скорости wx,wy,wz можно рассматривать как проекции на соответствующие координатные оси вектора w, определяющего угловую скорость вращения элементарного объема жидкости при его перемещении в трехмерном пространстве. Например, как было показано выше,
Обратим внимание на то, что буква z не входит в качестве индекса или координаты в правую часть равенства, определяющего wz. Аналогично записываются выражения для wz и wу. Вектор w в матричной форме имеет вид
В векторном анализе вместо w рассматривают вектор 2w, который обозначают rot u и называют вихрем вектора u (или вихрем скорости):
Следует обратить внимание, что ранее рассматривалось лишь перемещение объема за бесконечно малые интервалы времени Dt. Если рассматривать конечные интервалы времени, то, например, после поворота с угловой скоростью w за время Dt элементарный объем жидкости займет другие точки в поле скорости, и за следующий отрезок времени его угловая скорость может измениться. В результате даже при наличии во всех точках скорости Отметим, что, хотя мгновенная угловая скорость этого объема отлична от нуля,
при перемещении объема abсd на большое расстояние его поворот вокруг точки а не воспринимается как вращение. В том случае, когда все проекции скорости Проекция скорости vl на любое направление l определяется производной dj/dl . Необходимым и достаточным условием существования потенциальных течений являются равенства (
Следовательно,безвихревое течение жидкости потенциально.
ПОЛЯ В ГИДРОДИНАМИКЕ При изучении движения жидкости рассматривают её как сплошную среду. Таким образом, рассматривают не движение конечного числа отдельных частиц, а поля различных физических величин: скорости, плотности, давления и т.д. Такие поля можно назвать материальными полями. Математически эти поля описывают системой функций от координат и времени. Такой подход типичен не только для механики сплошных сред, но и для ряда других областей физики. В общем случае поле является пространственным (трёхмерным), иногда задачу упрощают, и рассматривают двумерные (плоские) или одномерные поля. В этом случае полагают, что физические величины зависят от одной или двух пространственных координат. Если физические величины не зависят от времени, то поле называют стационарным, в противном случае - нестационарным. При математическом описании полей предполагают, что существуют пределы значений физических величин в точке. Такой подход упрощает физическую реальность, так как не учитывает дискретность строения материи, но такая абстракция оправдана, нужно только разумно ограничивать область полученных результатов. Так как в практических задачах размеры обтекаемых тел намного порядков больше молекулярных размеров, то в этих задачах жидкость можно рассматривать как сплошную среду. Скалярным называют поле, которое в каждой точке пространства характеризуют одним числом. Скалярное поле описывают одной функцией, зависящей от трёх координат. (Например, поле плотности или температуры). Основное свойство скалярной функцииа(х1 ,х2 ,х3)состоит в том, что её численное значение не меняется при преобразовании координат. Если перейти от старой х1 ,х2 ,х3 к новой х¢1 ,х¢2 ,х¢3 системе координат, то значения плотности или температуры в фиксированной точке пространства, естественно, не изменяются: а (х¢1 ,х¢2 ,х¢3) = а (х1 ,х2 ,х3). Векторным называют поле, которое в каждой точке пространства характеризуется величиной и направлением. Например, поле скоростей жидкости. Вектор а1(х1 ,х2 ,х3), а2(х1 ,х2 ,х3), а3(х1 ,х2 ,х3), то есть, тремя функциями от трёх переменных. Это можно записать в виде матрицы-столбца:
а ÜÞ Введём новую декартову систему координат с тем же началом, но с другим направлением осей. Пусть lij - направляющий косинус оси x¢j относительно оси xi (i = 1,2,3; j = 1,2,3).Вычислим проекции того же вектора на новые оси координат:
a¢1 = l11 a1 + l21 a2 + l31 a3; a¢2 = l21 a1 + l22 a2 + l23 a3; a¢3 = l31 a1 + l32 a2 + l33 a3. Следовательно, вектор подчиняется определённому закону преобразования его компоненти отличается от скалярной величины, численное значение которой не меняется при преобразовании координат. То есть,сам вектор не меняется в новых координатах, а меняются его компоненты. Это выражение можно представить в индексной форме записи как сумму:
Или ещё более короткой При такой записи пользуются двумя правилами: 1. Соглашение о суммировании. По индексу, встречающемуся дважды (немой индекс), производят суммирование от 1 до 3. 2. Соглашение о ранге. Индекс, встречающийся один раз (свободный индекс), пробегает значения от 1 до 3. Таким образом, уравнение с одним свободным индексом означает запись трёх уравнений. Помимо скалярных и векторных полей в механике сплошной среды рассматриваются ещё и тензорные поля. Многие задачи физики и механики сплошной среды приводят к понятию тензора. Тензор, хотя и является обобщением понятия вектора, имеет гораздо более сложный характер. Разница заключается в том, что вектор просто интерпретируется геометрически, у тензора такого наглядного представления не существует. Описание происходит в прямолинейных (декартовых) системах координат. Координаты обозначаем х1, х2, х3, единичные векторы по осям - i1,i2, i3. Предположим, что в результате вращения осей координат как единого целого вокруг начала координат, мы перешли к новой системе координат Ox1´x2´x3´. Обозначим косинус угла между осями xi и x´k старой и новой системы aik = cos (x´i^xk). Для удобства пользования дальнейшими формулами приводим таблицу. Таблица 3.1
Теперь перейдём к определению тензора. Пусть каждому направлению Направлениям осей соответствуют векторы
Если векторы
то множество векторов Обозначим векторы, определяемые тензором для направлений новых осей
Эти условия равносильны (2.6.2) и их можно взять за новое определение тензора, если для каждой системы координат имеется тройка векторов Аналогичное определение можно дать и для вектора, если в уравнении (2.6.3) заменить векторы на проекции вектора. Поэтому тензор является обобщением вектора. Формулы (2.6.3) можно записать в сокращённом виде
Тензор определяется векторами
Из (2.6.1) и (2.6.3) можно получить формулы преобразования компонент тензора при переходе к новой системе координат:
где t´kl – компоненты в новой системе. Эти формулы можно также взять за определение тензора. Простейшими примерами являются нулевой и единичный тензоры. Согласно (2.6.4) у нулевого тензора в любой системе координат компоненты равны 0.
Для того, чтобы в дальнейшем не испытывать трудностей при использовании тензоров, запишем некоторые математические правила. ОПЕРАЦИИ НАД ТЕНЗОРАМИ
1. Умножение тензора на скаляр есть новый тензор, все компоненты которого умножены на этот скаляр (шаровой тензор):
2. Сумма тензоров есть новый тензор с компонентами, являющимися суммой одноимённых компонент слагающих тензоров. Так доля Т = Т´ + T´´ должна быть tik = t´ik + t´´ik. То, что такая сумма есть тензор, следует из линейности формул (4*). 3. Тензор, обладающий свойством tik = tki , называется симметричным. Если таблицу компонент такого тензора «повернуть» вокруг главной диагонали (то же, что и у определителя), то получится тот же самый тензор. 4. Пусть имеется тензор Т с компонентами tik .Составим таблицу с компонентами tki ( т.е. повёрнутую вокруг главной диагонали). Можно показать, что она также определяет тензор, который называется сопряжённым и обозначается Т*. Очевидно, что (T*)* = T. 5. Тензор, у которого tik = - tki, называется антисимметричным. Из определения следует, что tii = - tii, т.е. tii = 0 – компоненты главной диагонали равны 0. Антисимметричный тензор всегда можно записать в виде 6.Всякий тензор можно разложить на сумму симметричного и антисимметричного тензоров: Т = ½ (Т + Т*) + ½ (Т - Т*). Легко проверить, что в первой скобке стоит симметричный, а во второй – антисимметричный тензор. 7.Пусть дан тензор Т и вектор
8.Скалярное произведение тензора Т на вектор
9.Из приведённых определений операций ясно, что они должны обладать ассоциативностью и дистрибутивностью, т.е., например,
(Т1 + Т2 ( (l
Но коммутативностью эти операции не обладают, т.е. в общем случае ( 10.Пусть даны тензоры А, В с компонентами aik и bik. Скалярное произведение тензора А на тензор В (А, В)есть новый тензор Т, компоненты которого вычисляются по формулам:
Это определение совпадает с определением матричного умножения. Компонент tik получается умножением строки с номером i тензора А на столбец с номером j тензора В. Например, t23 = а21b13 + а22 b23 + а23 b33. 11.Скалярное произведение тензоров не обладает свойством коммутативности, т.е. вообще говоря, (А,В) ¹ (В,А). Перечислим некоторые свойства, которыми оно обладает:
(lА,В) = (А,lВ) = l (А,В); (l - скаляр); (А1 + А2, В) = (А1,В)+ (А2,В); (А,В1 + В2) = (А,В1) + (А,В2); [(А,В), С) = (А,(В,С)].

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 мысленно проведён какой-либо замкнутый контур L, ограничивающий некоторую поверхность S,то линейный интеграл
мысленно проведён какой-либо замкнутый контур L, ограничивающий некоторую поверхность S,то линейный интеграл
 ,
, - единичные векторы, направленные соответственно по касательной к Lи по нормали к поверхности S.
- единичные векторы, направленные соответственно по касательной к Lи по нормали к поверхности S. .
. .
. .
. . (3.5.1)
. (3.5.1) . (3.5.2)
. (3.5.2) Рис. 3.10. Сдвиговое продольно-однородное течение (течение Куэтта)
Рис. 3.10. Сдвиговое продольно-однородное течение (течение Куэтта)
 и rot u ¹ 0 (такие поля называются вихревыми) может оказаться, что при перемещении на конечные расстояния элементарного объема жидкости поворот его вокруг полюса не будет восприниматься как вращение в обычном смысле. Например, при сдвиговом продольно-однородном течении (течении Куэтта), представленном на рис. 3.10 с полем скорости
и rot u ¹ 0 (такие поля называются вихревыми) может оказаться, что при перемещении на конечные расстояния элементарного объема жидкости поворот его вокруг полюса не будет восприниматься как вращение в обычном смысле. Например, при сдвиговом продольно-однородном течении (течении Куэтта), представленном на рис. 3.10 с полем скорости  , имеем, что только
, имеем, что только  , а все остальные составляющие тензора grad u равны нулю.
, а все остальные составляющие тензора grad u равны нулю. ,
, , то есть
, то есть  ):
): .
. в пространстве трёх измерений может быть задан тремя компонентами:
в пространстве трёх измерений может быть задан тремя компонентами:


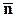 соответствует вектор
соответствует вектор  (не обязательно коллинеарный n).
(не обязательно коллинеарный n). , разложение которых опишем подробно:
, разложение которых опишем подробно: (3.6.1)
(3.6.1) , (3.6.2)
, (3.6.2) . Подставляя в предыдущее выражение (2.6.2) вместо
. Подставляя в предыдущее выражение (2.6.2) вместо  (3.6.3)
(3.6.3) , преобразующаяся по формулам (2.6.3) в тройку
, преобразующаяся по формулам (2.6.3) в тройку  , отвечающую другой системе координат, то этим определяется тензор.
, отвечающую другой системе координат, то этим определяется тензор. .
. .
. , (3.6.4)
, (3.6.4) .
. .
. .
.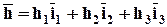 .Скалярное произведение тензора Т на вектор
.Скалярное произведение тензора Т на вектор  справа есть новый вектор
справа есть новый вектор  , обозначаемый (Т,
, обозначаемый (Т,  (i = 1,2,3).
(i = 1,2,3). , обозначаемый (
, обозначаемый (  .
. .
.