|
|
II.4. Взаимное расположение двух прямых на плоскости Лобачевского12
ДОКАЖИТЕ: Лемма: Если AB || CD, то существует ось симметрии прямых AB и CD.
ДОКАЖИТЕ: Теорема 6: Если AB || CD, то CD || AB.
Определение: Две ненаправленные прямые на плоскости Лобачевского параллельны, если на этих прямых можно выбрать направления так, чтобы они были параллельны. Определение: Две прямые на плоскости Лобачевского называются расходящимися (или сверхпараллельными), если они не пересекаются и не параллельны.
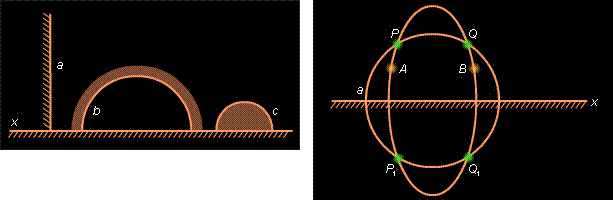
Через каждую точку, не принадлежащую прямой a, проходит бесконечно много прямых, каждая из которых расходится с прямой a.
Все прямые, не пересекающие прямую a, заполняют два вертикальных угла, ограниченных прямыми p и q. Граничные прямые p и q, не пересекающие прямую a, являются на плоскости Лобачевского параллельными прямой a и проходящими через A. Каждому направлению на прямой a соответствует своя параллельная прямая, проходящая через A.
Характерным свойством параллельных прямых на плоскости Лобачевского является то, что они неограниченно сближаются в направлении параллельности и неограниченно расходятся в противоположном направлении.
ВЫВОД: На плоскости Лобачевского имеются три случая взаимного расположения двух прямых: (1) прямые пересекаются; (2) прямые параллельны; (3) прямые расходятся.
ДОКАЖИТЕ: Теорема 7: На плоскости Лобачевского две прямые, имеющие общий перпендикуляр, расходятся.
Итак, характерное свойство расходящихся прямых – наличие у них единственного перпендикуляра. Следствие: На плоскости Лобачевского не существует общего перпендикуляра двух параллельных прямых.
III. Модель Пуанкаре планиметрии Лобачевского на евклидовой плоскости
Непротиворечивость системы аксиом доказывается представлением модели, в которой реализуются данные аксиомы. Модель планиметрии Лобачевского была предложена французским математиком Анри Пуанкаре в 1882 году.
Фиксируем на евклидовой плоскости E прямую x («горизонтальную») - «абсолют». Точки плоскости Лобачевского - точки плоскости E, лежащие выше абсолюта x. Плоскость Лобачевского – полуплоскость L, лежащая выше абсолюта. Прямые плоскости L - полуокружности с центрами на абсолюте или лучи с вершинами на абсолюте и перпендикулярные ему. Принадлежность точки прямой понимается так же, как и на евклидовой плоскости E. Отрезок плоскости L - дуга окружности с центром на абсолюте или отрезок прямой, перпендикулярной абсолюту (см. рис. 1).
Точка K лежит между точками C и D (если прямая плоскости Лобачевского - полуокружность) - K принадлежит дуге CD. В условиях нашей модели это эквивалентно тому, что K' лежит между C' и D', где C', K'и D' – проекции точек C, K и Dсоответственно на абсолют.
Рисунок 1
Два неевклидовых отрезка называют равными, если один из них неевклидовым движением можно перевести во второй. Неевклидово движение - преобразование L, которое является композицией конечного числа неевклидовых симметрий. Неевклидовы симметрии - инверсии с центром на абсолюте и осевые симметрии плоскости E, оси которых перпендикулярны абсолюту. Инверсия: Зафиксируем окружность W с центром O и радиусом R. Инверсией точки P относительно окружности W называется точка P1, лежащая на луче OP, такая, что OP×OP1 = R2.
Проверим справедливость некоторых аксиом Евклида и Лобачевского.
Аксиома I.1 (I.3). Каковы бы ни были две точки, существует прямая, проходящая через эти точки, и притом только одна.
Пусть даны точки A и B.
Рисунок 2
Рисунок 3 Аксиома II.1 (I.4): Из трех точек на прямой одна и только одна лежит между двумя другими. Справедливость аксиомы очевидна. Аксиома II.2 (IV.1): Прямая разбивает множество не принадлежащих ей точек плоскости на два подмножества (полуплоскости) так, что отрезок, соединяющий точки одной полуплоскости, не пересекается с прямой, а отрезок, соединяющий точки разных полуплоскостей, пересекается с прямой.
Неевклидовы полуплоскости изображены на рис. 4. Неевклидов отрезок, соединяющий две точки неевклидовой полуплоскости, не пересекает ее границы. Действительно, предположив противное, мы пришли бы к тому, что евклидовы окружности пересекались бы в четырех точках (рис. 5), что невозможно.
Рисунок 4
Рисунок 5
Аксиома III.1 (II.1): Каждый отрезок имеет определенную длину, большую 0. Если точка С лежит на отрезке AB, то длина отрезка AB равна сумме длин отрезков AC и BC.
1) Если неевклидов отрезок AB - евклидов отрезок (если прямая AB перпендикулярна абсолюту), то аксиома выполнена очевидно. 2) Если неевклидов отрезок AB - дуга окружности с центром на абсолюте. Рассмотрим инверсию i относительно окружности S с центром в точке O, пересечения неевклидовой прямой AB и абсолюта и радиусом R, равным OA > OB (рис. 6). Образ неевклидовой прямой AB - луч AB1, где A = i(A), B1 = i(B). Образ неевклидова отрезка AB - отрезок AB1 евклидова луча AB1.B1идовой прямой AB те очка O. Здесь O2 – вторая точка пересечения неевклидовой прямой AB и абсолюта. Так как AB1 является образом отрезка AB при неевклидовом движении, то они равны по определению и, следовательно, имеют равные длины.
Так как аксиома выполнена для евклидова отрезка AB1, то она выполнена и для неевклидова отрезка AB.
Рисунок 6 Аксиома III.2 (IV.2): Каждый угол имеет определенную градусную меру, большую 0. Развернутый угол равен 180°. Если луч с проходит между сторонами угла (ab), то градусная мера угла (ab) равна сумме градусных мер углов (ac) и (bc).
Возможные реализации углов в модели Пуанкаре для неевклидовых углов показаны на рис. 7. Из рисунка видно, что неевклидовыми углами являются угол между пересекающимися окружностями, а также между окружностью и пересекающей ее прямой. Угол между пересекающимися окружностями это – угол между касательными к ним прямыми, проведенными в точке пересечения. Угол между окружностью и пересекающей ее прямой – это угол между касательной к окружности в точке пересечения и прямой.
Рисунок 7
Величины углов на плоскости Лобачевского в модели Пуанкаре равны величинам соответствующих углов на евклидовой плоскости. Поэтому все свойства углов плоскости L можно увидеть на модели Пуанкаре. Отсюда достаточно очевидна справедливость аксиомы III.2. Аксиома параллельности Лобачевского: Пусть a - произвольная прямая, A - точка, не лежащая на прямой a. Тогда в плоскости, определяемой точкой A и прямой a, существует не менее двух прямых, проходящих через A и не пересекающих a.
Утверждение аксиомы параллельности Лобачевского выполняется не только для некоторой прямой a и некоторой точки A, не лежащей на a, но и для любой неевклидовой прямой a и любой не лежащей на ней точки A (рис. 8).
Рисунок 8
Если проверить и остальные аксиомы в модели Пуанкаре, то можно говорить о непротиворечивости геометрии (планиметрии) Лобачевского. Можно также обосновать независимость аксиомы параллельности от остальных аксиом планиметрии.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


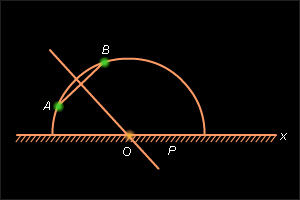 1) Прямая (евклидова) AB не перпендикулярна к абсолюту (рис. 2).
1) Прямая (евклидова) AB не перпендикулярна к абсолюту (рис. 2). 2) Прямая (евклидова) AB перпендикулярна абсолюту (рис. 3). Тогда ее часть, лежащая выше абсолюта, будет неевклидовой прямой, проходящей через точки A и B, поскольку p || x.
2) Прямая (евклидова) AB перпендикулярна абсолюту (рис. 3). Тогда ее часть, лежащая выше абсолюта, будет неевклидовой прямой, проходящей через точки A и B, поскольку p || x.