|
|
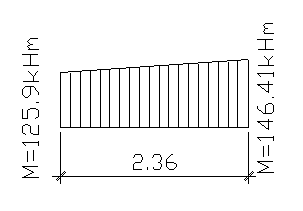
Расчет арок на устойчивость плоской формы деформирования.12 Определение нагрузок, действующих на арку На арку действуют следующие нагрузки: — нагрузка от собственного веса арки и веса покрытия; — снеговая нагрузка (в соответствии со снеговым районом); — ветровая нагрузка (в соответствии с районом). Постоянная нагрузка Таблица 2.1— Постоянные нагрузки, действующие на арку
Примечание: нормативное и расчетное значение нагрузки на арку от веса плиты принимаем из таблицы сбора нагрузки на плиту покрытия.
Нормативное значение от собственного веса арки:
где
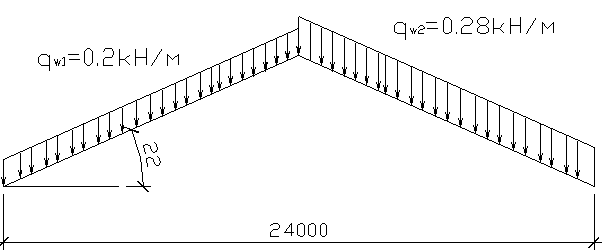
Линейно распределенные расчетные нагрузки на 1 м горизонтальной проекции арки, определенные с учетом шага арок (рис. 2.1):
Рисунок 2.1 Схема приложения на арку нагрузки от собственного веса и плиты покрытия с кровлей
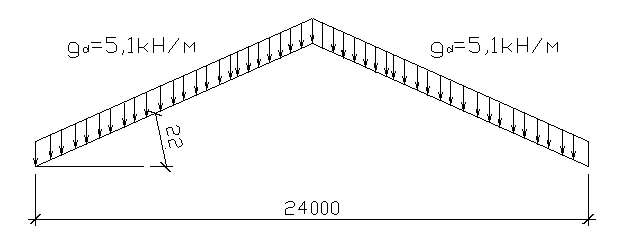
Линейно распределенные расчетные нагрузки на погонный метр арки от ее собственного веса и веса плиты покрытия с кровлей (рис. 2.2):
где l – пролет несущей конструкции (арки);
Рисунок 2.2 Схема приложения на арку постоянной нагрузки
Снеговая нагрузка
Конструкция располагается в г. Жлобине, для которого, согласно таблице 1.7[1], нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли S0 = 0,8 kПа (снеговой район IБ). Полное зачение веса снегового покрова на горизонтальную проекцию покрытия
Так как угол β = 22º, принимаем схему 1,вариант 1 (табл. 1.9 [1]). Коэффициент μ = 1 μ
Рис.2.3 Схема снеговой нагрузки
Согласно схеме снеговой нагрузки полное зачение веса снегового покрова на горизонтальную проекцию покрытия на арку
Расчетное значение снеговой нагрузки получаем умножением нормативного значения на коэффициент надежности для нагрузки 1,6, так как (п. 1.3.2, [1])
где
Линейно-распределенные расчетные нагрузки на 1 м2 арки от веса снегового покрова (рис. 2.4):
Рисунок 2.4 Схема приложения на арку нагрузки от снегового покрова
Ветровая нагрузка.
Нормативное значение средней ветровой нагрузки на высоте z над поверхностью земли определяем по формуле
где
Так как при высоте конструкции 4,8м. то коэффициент k, принимаем с запасом – k = 0,5.
с– аэродинамический коэффициент, (табл. 1.12 [1]). Коэффициент надежности для ветровой нагрузки
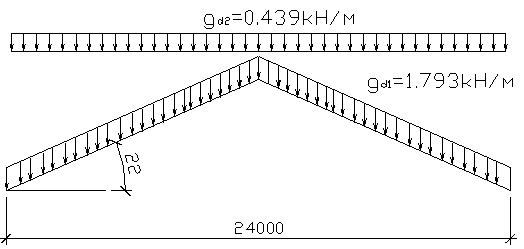
Расчетная ветровая нагрузка на 1м арки по участкам:
Рисунок 2.5 Схема приложения на арку ветровой нагрузки
Статический расчет арки
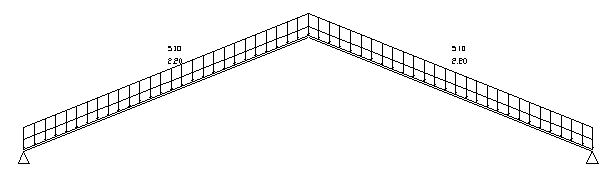
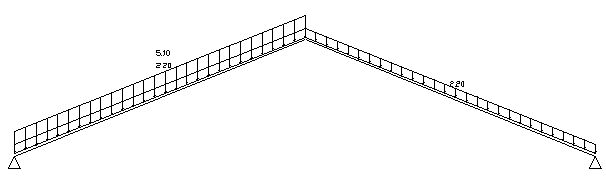
Произведем расчет арки по следующим сочетаниям нагрузок: 1. Постоянная нагрузка + снеговая нагрузка на весь пролет; 2. Постоянная нагрузка + снеговая нагрузка на половине пролета; 3. Постоянная нагрузка + снеговая нагрузка на весь пролет + ветровая с коэффициентом сочетания 0,9 [1]; 4. Постоянная нагрузка + снеговая нагрузка на половине пролета + ветровая с коэффициентом сочетания 0,9. Статический расчет арки выполняем в программном комплексе “Raduga”. Основная система: статически определимая трехшарнирная арка.
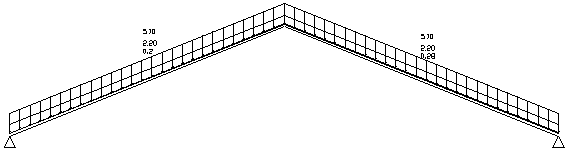
Рисунок 2.6 Постоянная нагрузка + снеговая нагрузка на весь пролет
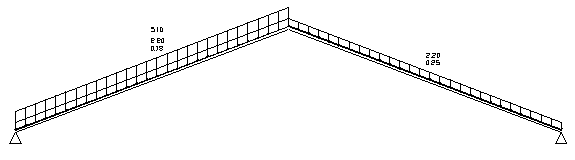
Рисунок 2.7 Постоянная нагрузка + снеговая нагрузка на половине пролета
Рисунок 2.8 Постоянная нагрузка + снеговая нагрузка на весь пролет + ветровая с коэффициентом сочетания 0,9 (расчетная комбинация)
Рисунок 2.9 Постоянная нагрузка + снеговая нагрузка на половине пролета + ветровая с коэффициентом сочетания 0,9
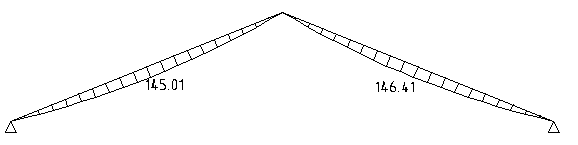
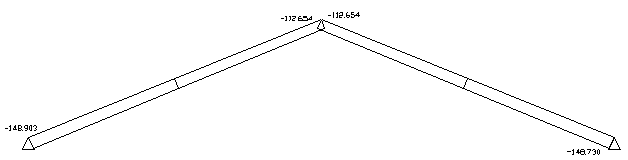
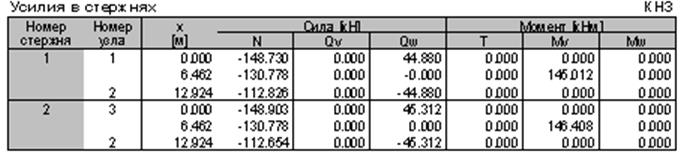
Максимальный изгибающий момент возникает при загружении арки постоянной нагрузкой, снеговой нагрузкой на арку и ветровой. Внутренние усилия возникающие в сечениях арки представлены в табл. 2.2.
Рисунок. 2.10 Эпюра изгибающих моментов от расчетной комбинации нагрузок
Рисунок. 2.11 Эпюра продольной силы от расчетной комбинации нагрузок
Таблица 2.2 Внутренние усилия в стержнях арки.
Максимальный изгибающий момент
2.3 Конструктивный расчет
Для изготовления арок принимаем пиломатериал из древесины породы лиственница кроме европейской и японской II сорта толщиной 40мм с последующей острожкой на 6мм (табл.1.1[1]) и шириной 225мм. Оптимальная высота сечения арки находится в пределах:
Принимаем поперечное сечение арки 225мм´680 мм из 20 слоев толщиной 34мм. После изготовления клееный пакет фрезеруется с фугованием по ширине на 10мм. (табл.1.3[1]). Таким образом принимаем окончательные размеры клееного пакета 215мм´680мм – Ad= 146200 мм2; Расчетное сопротивление сжатию и изгибу fm.d=fc.o.d=15МПа (табл. 2.4 [1]). Коэффициент условий работы kmod= 1,2 (табл. 2.6 [1]); при h=680мм kh=0,936 (табл. 2.7 [1]); при d=34мм kd = 0.994 (табл. 2.8 [1]); ks = 0.9 (п. 2.1.2.10 [1]); kx = 1,2 (табл. 2.5 [1]). С учетом коэффициентов расчетные сопротивления сжатию и изгибу равны
fc.o.d= fm.d= 15×1,2×0,936×0.994×1,2×0,9 = 18.09МПа.
Расчет арки на прочность Расчет арки на прочность выполняем как сжато- изгибаемого элемента в соответствии с п. 3.3, стр. 263 [1]:
где
где - Коэффициент, учитывающий увеличение напряжений при изгибе от действия продольной силы, определяем по формуле:
где Гибкость
где ld=lm=12,97 м(табл. 7.10 /2/) - расчётная длина;
Так как
Тогда Коэффициентkinst определяем по формуле 7.24 /2/:
Расчет арок на устойчивость плоской формы деформирования. Покрытие из плит шириной 1,180м раскрепляет верхнюю кромку арки. Устраиваем раскосы через 2 плиты, lm=2,36м. Расчет арок на устойчивость плоской формы деформирования производим по формуле:
где
где Гибкость
где
Так как
Тогда
Коэффициент
где lm=2360 мм – расстояние между промежуточными точками от смещения из плоскости изгиба;
Подставив найденные значения, получим:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
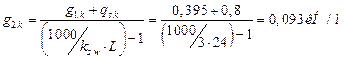 ,
, - постоянная нормативная нагрузка от покрытия;
- постоянная нормативная нагрузка от покрытия; - полное нормативное значение снеговой нагрузки;
- полное нормативное значение снеговой нагрузки;  - расчетный пролет;
- расчетный пролет; - коэффициент собственного веса конструкции.
- коэффициент собственного веса конструкции. ;
; 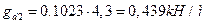
 ;
; - длина дуги арки.
- длина дуги арки.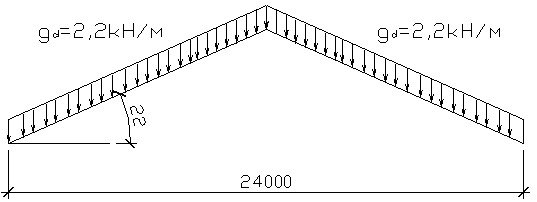
 определяем по формуле [1]
определяем по формуле [1]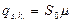
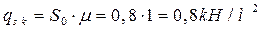
 ;
;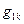 - нормативное значение равномерно распределенной нагрузки от веса покрытия, kH/м2;
- нормативное значение равномерно распределенной нагрузки от веса покрытия, kH/м2; - нормативное значение веса снегового покрова, kH/м2 .
- нормативное значение веса снегового покрова, kH/м2 .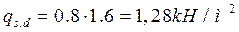
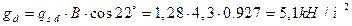
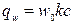
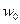 - нормативное значение ветрового давления, принимаемое в зависимости от ветрового района (табл. 1.10 [1]); w0 = 0,23кН/м2 – скоростной напор ветра для I района;
- нормативное значение ветрового давления, принимаемое в зависимости от ветрового района (табл. 1.10 [1]); w0 = 0,23кН/м2 – скоростной напор ветра для I района; - коэффициент, учитывающий изменение ветрового давления по высоте (табл. 1.11 [1]) дляместности типа B;
- коэффициент, учитывающий изменение ветрового давления по высоте (табл. 1.11 [1]) дляместности типа B; ;
;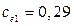 ;
;  ; при h1/l = 0,2 и α = 22º
; при h1/l = 0,2 и α = 22º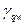 принимаем равным 1.4 [1].
принимаем равным 1.4 [1]. ;
;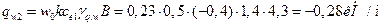 .
.
 , соответствующая продольная сила -
, соответствующая продольная сила -  , поперечная сила -
, поперечная сила - 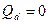 при комбинации: постоянная нагрузка + снеговая нагрузка на весь пролет + ветровая с коэффициентом сочетания 0,9 (расчетная комбинация)
при комбинации: постоянная нагрузка + снеговая нагрузка на весь пролет + ветровая с коэффициентом сочетания 0,9 (расчетная комбинация)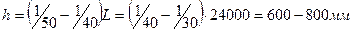 .
.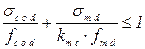
 - расчетное напряжение сжатия;
- расчетное напряжение сжатия;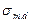 - расчетное сопротивление изгиба;
- расчетное сопротивление изгиба; - коэффициент, учитывающий увеличение напряжений при изгибе от действия продольной силы;
- коэффициент, учитывающий увеличение напряжений при изгибе от действия продольной силы; - расчетное сопротивление сжатию;
- расчетное сопротивление сжатию; - расчетное сопротивление изгибу.
- расчетное сопротивление изгибу.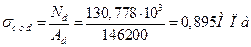
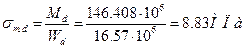
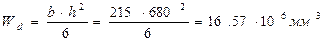 .
.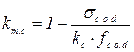
 ;
; арки:
арки: ,
,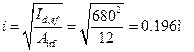 - радиус инерции сечения элемента в направлении соответствующей оси;
- радиус инерции сечения элемента в направлении соответствующей оси; :
: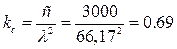
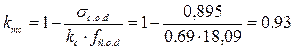
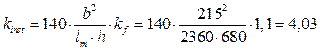
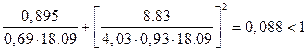 - таким образом, условие устойчивости выполнено и дополнительных раскреплений арок не требуется.
- таким образом, условие устойчивости выполнено и дополнительных раскреплений арок не требуется. ,
, - показатель степени, учитывающий раскрепление растянутой кромки из плоскости -
- показатель степени, учитывающий раскрепление растянутой кромки из плоскости -  - коэффициент продольного изгиба, определяемый для участка длиной
- коэффициент продольного изгиба, определяемый для участка длиной 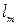 между закреплениями
между закреплениями - расчетное сжимающее напряжение;
- расчетное сжимающее напряжение; - расчетное напряжение от изгиба;
- расчетное напряжение от изгиба; - коэффициент продольного изгиба, учитывающий увеличение напряжений при изгибе от действия продольной силы, определяем для участка длиной
- коэффициент продольного изгиба, учитывающий увеличение напряжений при изгибе от действия продольной силы, определяем для участка длиной  между закреплениями по формуле:
между закреплениями по формуле: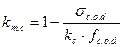
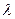 арки:
арки: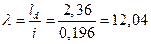
 ;
; - радиус инерции сечения арки;
- радиус инерции сечения арки;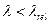 - то
- то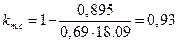
 определяем по формуле:
определяем по формуле: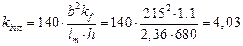
 - ширина поперечного сечения;
- ширина поперечного сечения; - максимальная высота поперечного сечения на участке
- максимальная высота поперечного сечения на участке 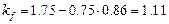 - коэффициент, зависящий от формы эпюры изгибающих моментов на участке
- коэффициент, зависящий от формы эпюры изгибающих моментов на участке