
|
|
Система счисления в остаточных классах(СОК)Главное отличие системы остаточных классов заключается в том, что у нее имеется не одно , а несколько оснований: bi=(b1,b2,...,bn), причем i-я цифра xi любого числа Х представляет собой остаток от деления исходного числа на i-е основание bi: Единственное ограничение, налагаемое на величины основания bi, заключается в том, что все bi должны быть взаимно-простыми числами.
Если b1=3 b2=5, то
0 0 0 1 1 1 2 2 2 3 0 3 4 1 4 5 2 0 6 0 1 7 1 2 8 2 3 9 0 4 10 1 0 11 2 1 12 0 2 13 1 3 14 2 4 15 0 0
Полученное сочетание остатков можно принять для изображения (кодирования) чисел в разрешенном диапазоне. Диапазон представления В отличии от позиционных систем счисления в СОК нет межразрядных связей, т.к. цифры в каждом разряде образуются независимо друг от друга. Остаток от деления А на число N: A(mod N)=R Пусть b=7, рассмотрим A=15 B=21 Остаток по модулю 7 А(mod 7)=15(mod 7)=1 B(mod 7)=21(mod 7)=0 Если C=A+B=15+21=36, то C(mod 7)=36(mod 7)=1 (1). т.е. C(mod 7)=(A+B)(mod 7)=A(mod 7)+B(mod 7) Это можно доказать: A+B=C Аналогично (2). Если C=A*B, то C(mod 7)=(A*B)(mod 7)=A(mod 7)*B(mod 7) 15=3*5 15(mod 3)=15(mod 5)=0 При этом если сумма (если произведение) остатков превышает модуль dm, то она (или оно) тоже берется по модулю dm (делится на dm).
Следовательно, все арифметические действия (за исключением деления) над числами в СОК являются поразрядными и производятся по простым правилам. При этом сами цифры (т.е. остатки) в СОК можно изображать в двоичной системе счисления. В результате этого реализация алгоритмов с малым содержанием операции деления в СОК обеспечивает значительное повышение скорости обработки информации по сравнению с реализацией тех же алгоритмов в двоичной системе.
Пример: 1.Сложить числа в двоично-кодированной СОК с основаниями b1=3 b2=5 b3=7 38+47 38(mod 3)=2 38(mod 5)=3 38(mod 7 )=3 X1 =3810=233(10/COK)=(10; 011; 011) (2/COK) 47(mod 3)=2 47(mod 5)=2 47(mod 7)=5 X2=4710=255(10/COK)=(10; 010; 101)(2/COK)
X1 (10; 011; 011) + X2 (10; 010; 101) X3 (01; 000; 001) (2/COK)
Проверка: 3810+4710=8510 85(mod 3)=1 85(mod 5)=0 85(mod 7)=1
В СОК наиболее просто и экономично строятся реверсные счетчики, т.к. при увеличении или уменьшении некоторого числа на 1 все остатки от деления также соответственно увеличатся на 1. Если при увеличении числа некоторый остаток имеет величину bi-1, то он заменяется в следующем шаге на 0. При уменьшении числа остаток, равный 0 заменяется на bi-1.
Недостатки СОК
1. Относительная сложность операции деления. Обычно деление сводится к определению обратной величины делителя Х по итеративной формуле 2. Значительная сложность перевода чисел из принятой позиционной системы в СОК и обратно. Прямое деление на все основания для получения цифр практически не используется (не эффективно и долго). На практике, т.к. в машине уже есть арифметическое устройство, работающее в СОК, для перевода чисел пользуются наборами всех цифр и нужных степеней основания исходной (например, десятичной) систем, представляемых в СОК. Так для перевода числа 1410 в СОК с основанием bi=3;5 нужны такие константы: 100=1=(1;1) 4=(1;4) 101=10=(1;0) Тогда 1410=1*101+4*100=(1;1)*(1;0)+(1;4)(1;1)=(1;0)+(1;4)=(2;4) Обратное преобразование еще более сложно 3. Относительная сложность сравнения чисел в СОК, поскольку их поразрядное сравнение ничего не дает. 4. Отсутствие удобных способов определения переполнения разрядной сетки машины результатом некоторой операции, т.к. все операции в СОК являются поразрядными.
В следствии этого СОК получил применение в основном в специализированном ЭИВМ, в которых необходимо высокое быстродействие, диапазон изменения чисел фиксирован, а операция деления встречается редко.
Контроль по модулю. Разнообразные задачи можно решать с помощью метода контроля по модулю, основанного на свойствах сравнения
1. A1=B1(mod p) A2=B2(mod p) (A1+A2)mod p=B1(mod p)+B1(mod p) 2. A=B(mod p) C=B(mod p) 3. A1=B1(mod p) C=B2(mod p) (AC)mod p=B1B2(mod p) 4. A=B(mod p) Am=Bm( mod mp) 5. A=B(mod p) An=Bn(mod p) 6.
Существуют два метода получения контрольного кода: числовой и цифровой
Числовой метод контроля
Код числа определяется в ССОК с mod P rA=A-[ Если p=q (основанию СС), то контролируется только младший разряд (плохо). Аналогично для m<n p=qm контролируется m младших разрядов Контроль на основании выполнения операций в ССОК Неудобство: получение rA
Цифровой метод контроля При цифровом методе:
Контрольный код получают : 1) непосредственным делением 2) суммированием цифр по mod p (Второй способ легче)
Однако при цифровом методе свойства сравнений не всегда справедливы из-за наличия переносов (заемов) при арифметических действиях. Поэтому контрольный код результата операции находят с коррекцией. Но можно выбрать такой модуль, что коррекция не нужна. Очевидно, это будет если:
rA=A mod p
т.е. т.е Это возможно, если aiqi=ai(mod p) т.е. qi=1(mod p) т.е. q=mp+1, где m-целое число
Но тогда
Анализ показывает, что для двоичной СС (q=2) целого p нет. Это значит, что контролируемую информацию надо представлять в некоторой промежуточной СС.
К модулю p представляют требования: 1) величина mod p должна быть такой, чтобы возникновение ошибки нарушало сравнимость кодов. 2) образование контрольного кода должно осуществляться простыми средствами 3) величена mod p должна быть по возможности небольшой, чтобы не возрастал объем вспомогательного оборудования.
Т.к. в ЭВМ информация представляется символами двоичного алфавита, то для контроля целесообразно перейти к системам с основанием q=2S (S Переход от двоичного представления исходной информации к новому представлению с основанием q=2S осуществляется разбиением информации на группы по S разрезов с последующим суммированием этих групп по модулю p=(2S-1)/m или при m=1 p=2S-1 Модули для контроля p=3 (m=2, s=2, p=3) p=7 (m=1, s=3, p=7)
Пример: контроль по mod 3 Контролируемая информация представляется символами 4-й системы с последующим суммированием по mod 3 диад (свертывание). Требуется двухразрядный двоичный сумматор с цепью циклического переноса из старшего разряда в младший. A=46=1011102 B=29=0111012

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ><0]
><0] ; Но
; Но 
 с последующим умножением найденного значения на делимое.
с последующим умножением найденного значения на делимое.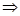 A=C(mod p)
A=C(mod p) (mod p)
(mod p) ]
] или
или 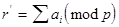 , где ai-цифра числа
, где ai-цифра числа на mod p
на mod p
 , но A=
, но A= 

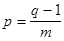
 2): 4,8,16
2): 4,8,16