
|
|
Основные величины, изучаемые в нач шк. Длина отрезка и единицы длины.12 Величина – св-ва предметов поддающихся качественной оценке. Изучаются: длинм, масса, емкость, площадь, время, скорость. Изучение - по некому единому плану. 1)выяснение представлений шк. о данной величине. 2)сравнение объектов разными способами а)на глаз, б)наложение в)приложение г)через посредники. 3)рассмотрение данной величины. 4.Введение единиц измерения величин в соответствии в кол. центрами т.е. изучением нумерации. 5)выполнение арифмет. операций а)сложение и вычитание именованных чисел 15м-это именованное число. – в строчку и столбик. б)умножение. именов числа на число. в)деление именованных чисел. на число. 6)решение задач связанных с величинами. 7)перевод из 1 ед. в единицу др. наименования. Длина. Наглядность (сравнение). Мерка (отрезок любой длины). Сравнение длин с разными мерками (не верно). Общая мерка – ед длины (см). Измерение с помощью линейки. Сложение и вычитание отрезков (на луче; с имен числами).
10. Умножение - одно из основных арифмет действий, это опереция, где первый аргумент складывается столько раз, сколько показывает второй. Деление - арифмет действие, обратное умножению. Деление - такая операция, в результате кот получается число, кот при умножении на делитель даёт делимое. Для усвоения системы умножения полезно использовать примеры сравнения, выбора, преобразования, предлагая различные виды задания: а) на соотнесение рисунка и математической записи (прочитай записанные под рисунком выражения и догадайся, что обозначает в каждом произведении 1 и 2 множитель). б) на выбор рисунка соответствующего данной записи. После ознакомления учащихся со смыслом умножения, учащиеся должны уметь читать выражения разными способами: 2*5 - 2 повторить 5 раз, по 2 взять 5 раз, 2 умножить на 5, 2 увеличить в 5 раз, первый множитель 2, второй - 5, найти произведение. Основой формир у мл шк представлений о смысле деления служит теоретика-множественный подход к трактовке частного, суть кот сводится к разбиению конечных множеств на равночисленные подмножества, не имеющие общих элементов. Выбор этого подхода обусловлен тем, что он позволяет опираться на жизненный опыт ребенка при введении новой терминологии и математической записи. Большинство учащихся легко справляются с таким практическим заданием: раздай 10 яблок по 2 на каждую парту. Смысл действия деления сводится к разбиению конечного множества яблок на равночисленные подмножества (по 2 яблока). В результате получается число частей в этом разбиении, т.е разделить яблоки на части, по 2 яблока в каждой, т.е узнать, сколько по 2 содержится в 10.вводится новая запись 10:2=5. дальше учитель знакомит детей с компонентами (делимое, делитель, частное). Дети знакомятся с 2 способами деления:1) деление на части, 2) деление по содержанию. Табличные случаи умножения: изучение таблицы умножения явл-ся центральной задачей обучения матем во 2 и 3 классе. К таблице умножения относят случаи умножение однозначных натуральных чисел на однозначные натуральные числа. Изучению таблиц на 2,3,4 помогают иллюстрации. При значении второго множителя больше 5, используется прием прибавления к предыдущему результату (2*6= 2*5+2=12). Следующим приемом - перестановка множителей. Здесь дети знакомятся с таким законом: от перестановки множителей произведение не меняется. Табличное деление: в нач. школе действие деление рассматривают как действие обратное умножению. Сначала дети знакомятся со случаями деления без остатка в пределах 100. На основе таблицы умножения составляется таблица деления. Множ. Способы задания. Отношения, операции и их св-ва.Понятие множества не определяется через др понятия. Пример: буквы алфавита (конеч), рыбы в океане (бескон), N числа (бескон), Русские цари (конеч). Элементы множ - объекты, из кот состоит множ. Множ обозначают большими буквами лат алфавита, его элементы - маленькими. Множ В – подмнож А, если каждый элемент множ В является элем множ А. Равн множ – если АсВ и ВсА. Виды множ: Пустое - множ, не содержащее ни одного элемента. Классифик: конечные, бесконечные. Основ числ. множ: N, R(действ), Z(целые), J(иррац), Q(рацион), C(комплексные). Основ способы задания: перечисл, указание хар-го св-ва и описание его элементов. Отнош м\у множ: объединение - содерж все элементы, кот принадлежат множеству А или множ В (А∪ В). Св-ва: 1) коммутат: А∪В=В∪А. 2) ассоциат: (А∪В)∪С=А∪(В∪С). 3) А∪∅=А (пустое множество - нейтральный элемент). 4) А∪U=U (U - поглощ элемент). 5) Если В⊂А, то А∪В=В. пересечение - содерж все элементы, кот принадлежат множ А и множ В (А∩В). Св-ва: 1) коммутат: А∩В= В∩А. 2) ассоциат: (А∩В)∩С= А∩(В∩С). 3) А∩∅=∅. 4) А∩U=А. 5) Если В⊂А, то А∩В=А. Операции ∪ и ∩ связаны законами дистрибут или распределит св-ми: (А∪В)∩С=(А∩С)∪ (В∩С) и (А∩В)∪С= (А∪С)∩ (В∪С). Разность - содерж только те элементы, кот принадлежат множ А и не принадлежат множ В (А\В). Дополнение - Пусть В с А. В этом случае разность множ А и В – дополнение В до множ А (В'А). Св-ва разности и дополн: 1) (А\В)\С=(А\С)\В. 2) (А∪В)\С=(А\С)∪(В\С). 3) (А\В)∩С=(А∩С)\(В∩С). 4) (А∪В)' =А'∩В'. 5) (А∩В)'= А'∪В'. Св-ва отнош м\у множ: 1) равенства: а) рефлексивность (= самому себе); б) симметр (А=В, то В=А); в) транзит (А=В, В=С => А=С); г) эквивал. 2) включение: а) транзит (А⊂В и В⊂С, А⊂С); б) асимметр (А⊂В => В⊂А). 3) пересеч: а) рефлект; б) транзит.
Теор-множ подход к определению * и : для целых неотриц чисел.Определение «*» N чисел в аксиомат теории основывается на понятии отнош «непосред следовать за» и сложение. Т: Если b больше, то произведение чисел а и b равно сумме в слагаемых, каждое из котх равно а. Если а и b N числа и b больше 1, то аb можно рассматривать как сумму в слагаемых, каждое из кот равно а. Умножение на 1 определяется так: а*1=а. С теоретико–множ позиции а*b представляет собой число эквивалентов в объединении b множеств, каждое из кот содержит по а элементов и никакие два из них не пересекаются. Законы: Коммутат аb=ba. Ассоциат (a*b)c= a(b*c). Дистрибут (а+b)*c =ac+bc. Т: Произвед а и в существует и единственно. Док-во: 1) в > 1 по определению а * в – есть сумма в слагаемых, каждое из кот равно а, так как сумма существует и единственна, то существует и единственно и произвед. (докаж.что 2*3=6. 1сп. 3>1,то 2*3=2+2+2=6 ч.т.д.) 2) в = 0, если в = 0, то по определению а * 0 = 0, так как 0 существует и единственен, то существует и единственно произвед а * 0. 3) в = 1, если в = 1, то по определению а * 1 = а, так как а существует и единственно, значит существует и единственно произведение а*1. В аксиомат теории, «:» - операция, обратная умножению. С теор–множ подхода деление чисел оказывается связанным с разбиением конечного множества на равночисл попарно непересекающиеся подмножества и с его помощью решаются две задачи: деление на равные части и по содержанию. Т: Сущ. Каковы бы ни были два целых неотрицательных числа а и в всегда найдется целое неотрицательное число с, которое является их суммой. Т: Един. Каковы бы ни были два целых неотрицательных числа а и в, существует единственное число с, которое является их суммой. Деление c остатком – арифмет операция, вид операции деления, результат кот - два целых числа: неполное частное и остаток от деления целого числа на др целое число.
Величина – св-ва предметов поддающихся качественной оценке. Изучаются: длинм, масса, емкость, площадь, время, скорость. Изучение - по некому единому плану. 1)выяснение представлений шк. о данной величине. 2)сравнение объектов разными способами а)на глаз, б)наложение в)приложение г)через посредники. 3)рассмотрение данной величины. 4.Введение единиц измерения величин в соответствии в кол. центрами т.е. изучением нумерации. 5)выполнение арифмет. операций а)сложение и вычитание именованных чисел 15м-это именованное число. – в строчку и столбик. б)умножение. именов числа на число. в)деление именованных чисел. на число. 6)решение задач связанных с величинами. 7)перевод из 1 ед. в единицу др. наименования. Скорость (3 класс) – путь пройденный тела за единицу времени. Трудно объяснить запись, дать наглядное представление. При знакомстве – сравнение (машина и человек, самолет и поезд). Введение формулы (V=S:t, t=S:V, S=V*t). Составление модели (рисунок). Решение - от данных к вопросу. Движение: 1. В разных направлениях (встречное, в противоположном направлении); 2. в одном направлении (одновременное, вдогонку, с отстованием).Площадь – св-во фигуры занимать измеряемое место на плоскости. Наглядное сравнение. Измерение: 1.введение единичного квадрата (S не важна). 2.палетка (приближ рез-т). 3.ед.измерения. Указание других мер измерения (ар, га) Время. Невозможность наглядности – жизненный опыт (сравнение: сезоны, урок/перемена, …). Измерение времени с помощью часов (солнечные, водные, песочные, механ, электр). Демонстрация ходов стрелок часов (час – по цифрам, минута – по делениям). Знакомство с циферблатом. Единицы времени. Название времени (1 час 15 минут = 15 минут второго = …). С такими единицами времени, как год, месяц, неделя учащиеся знакомятся с использованием календаря. По нему определяется сколько месяцев в году, как они называются, с какого месяца начинается год определяют кол-во дней в каждом месяце. Действие со временем (сложность – не 10 сист счисления).
15. НОД и НОК двух чисел. Разложение чисел на простые множ.Общий делительN чисел а и b - число, которое является делителем каждого из данных чисел. Наиб число из всех делителей чисел а и b - НОД. Н-р: Возьмем два числа 12 и 8 и выпишем их делители. Число12 делится на 1,2, 3, 4, 6, 12. Число 8 делится на 1, 2, 4, 8. У чисел общие делители -1, 2 и 4. Наиб - 4. Его называют НОД чисел 12 и 8. Св-ва НОД: 1. НОД N чисел всегда сущ и является единственным. 2. НОД чисел а и b не превосходит меньшего из данных чисел, т.е. если a < Cb, то О (а,b ):а . 3. НОД N чисел а и b делится на любой общий делитель этих чисел. Возьмем опять два числа 12 и 8 и выпишем несколько кратных чисел. Числа, кратные 12: 12, 24, 36, 48, 60, 72, 84; числа, кратные 8: 8, 16, 24, 32, 40, 48, 56, 72, ... Общие кратные - 24, 48, 72. Наим – 24. Его называют НОК чисел 12 и 8. Общее кратное N чисел а и b - число, которое кратно каждому из данных чисел. Наименьшее число из всех общих кратных чисел а и b - НОК этих чисел. Св-ва НОК: 1. НОК N чисел а и b всегда сущ и является единственным. 2. НОК чисел а и b не меньше большего из данных чисел, т.е. если а >b , то К (а,b ):а . 3. Любое общее кратное двух N чисел а и b делится на НОК этих чисел.
17. Понятие дроби.В мл.кл. ведение дробей связано со счетом и измер долями. Понятие дробь: Пусть даны е-един отрезка, а-отрез, причем е - сумма n-отрезков = е1. Если а сост из m отрез=е, то его длина = m/n*e, где символ m/n –дробь. m-числитель, n-знаменатель, /-дроб черта замен делением. Т. Для того чтобы дроби и выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство mg = np. Две дроби m/n и p/q называются равными, если mg = np. Если дроби равны, то пишут m/n = p/q. Из сформулир выше теоремы и определения следует: две дроби равны тогда и только тогда, когда они выражают длину и того же отрезка. Нам известно, что отнош равенства дробей рефлексивно, симметрично и транзитивно, т.е. является отнош эквивалентности.Т. Равенство дробей является отнош эквивалентности. Осн св-во дробей: Если числ и знам * или / на одно и то ж число, то получится дробь = данной (на этом св-ве основано сокращ дробей и приведение к одному знамен). Сокращ дробей - замена на друг = данной, но с меньшим числ и знам (т.е. более круп доли). Не всяк можно сократить (если числ и знам взаимно просты) - несократ. Привед к общ знам - замена = дробями, имеющ один знам (размельчение дробей). Рацион числа –это положит и отриц числа (целые и дробные) и 0. Св-ва: 1) нет наим и наиб чисел, 2) огранич снизу 0, сверху неогран, 3)плотно, 4) бесконечно, 5) упорядоченно, 6) замкнуто относ «+», «*», «:», 7) множ Q+ и Q – счетны (если эквивал множ N числ). Счетное множ – м/у ним и множ N можно установить соотв.Т: Множ неотр Q чисел счетно. Д-во: представим кажд Q число в виде дроби.
19. Высказывание - любое повествовательное предложение, о кот можно сказать, истинно оно или ложно. Обозначают заглавными буквами лат. алфавита, н-р А, В, С, … Отрицанием - высказ А, которое И, если А Л, и Л, когда А И. Конъюнкция 2х высказ A и B - высказ с помощью союза «и», И когда оба И, Л – когда хотя бы одно Л. Дизъюнкция 2х высказ A и B - высказ с помощью союза «или», И когда хотя бы одно И, Л – когда оба Л. Св-ва V и ^: Коммутативность: АVB=ВVA (А^B=В^A). Ассоциативность: (AVB) VC=AV (BVC).( (A^B)^C=A^(B^C) ) AVÃ=и. (A^Ã=л) Дистрибут: AV(B^C)=(AVB)^(AVC). Импликация – высказ образованное при помощи союзов «если, то». Л, когда А - И, а В - Л. В остальных случаях - И. А – условие, В – заключение. А=>В – данное; В=>А – обратное данному; Ã=>неВ - противопол данному; неВ=>Ã – противопол обрат. Эквиваленция - высказ образованное «тогда и только тогда, когда». И – когда оба И. А^BóB^A; AVBóBVA. Два составных высказывания A и B - равносильны (или эквивалентны), если они одновременно И или одновременно Л при любых предположениях об истинности входящих в них элементарных высказываний. Записывают: A=В. Предикат - матем предложение c одной и более переменных, обращающееся в высказывание при подстановке знач D(f) одномест предиката – множ знач, кот принимает переменная х. Множ истинности (Т) – множ знач переменной из D(f), при подставлении кот предикат становится И высказ. Равносильные предикаты – два предиката A(x) иB(x) заданные на множ Х и имеющие одинаковые множ истинности. Операции: 1.Отрицание - предикат Ã(x) И при знач хєХ, при кот предикат A(х) Л и наоборот. 2. Конъюнкция - предикат Р(х)^Q(x), обращающийся в И высказывание при знач хєХ, при кот оба предиката И. 3.Дизъюнкция - предикат Р(х)VQ(x), обращающийся в И высказывание при знач хєХ, при котх хотя бы один предикат И. 4.Импликация - предикат Р(х)=>Q(x), обращающийся в Л высказывание при тех знач хєХ, при кот Р(х) - И, а Q(x) – Л. 5. Эквиваленция- предикат Р(х)ó Q(x), принимающий знач И при тех знач хєХ, при кот знач множ истинности совпадают.
18. Текстовая задача – описание некоторых ситуаций на естеств языке с требованием дать коллич хар-ку какого-либо компонента этой ситуации. 2 части: условие – непосредственно ситуация (данное); требование – указание того, что нужно найти (искомое). Методы решения: арифмет (действия), алгебр (уравнения), логич (рассужд, граф, таблицы), геометрич (рисунок), практич. Составные задачи (2 и более действий): -без тройки взаимод единиц (t,V,S); -с пропорц величинами: ·нахождение четвертого пропорц, ·нахожд неизвестного по 2м разностям, ·пропорц деление, ·на движение. Этапы реш: ознакомление с содержанием; поиск решения; модели, изображ; план решения; запись решения; прочтение вопроса; запись ответа; проверка решения (подстановка, др способы, различ методы, прикидка, обрат задача). Задачи по классам: модель (символ, естеств), график, чертеж, графические (рисунок, схема), граф, таблица, вербальная модель, предметная модель. Для введения задач на пропорц данные используются дид. игра «магазин» ее цель сформировать понятие цена, кол-во и стоимость. Прямая и пропорциональная зависимость означает что при постоянном из 1 величин с увеличением др. величины увеличивается др. величина. Для того чтобы рассмотреть прямую и пропорциональную зависимость школьнику предлагается заполнить таблицу (цена, кол, стоимость) и дети сами заполняют значения – прослеживают измениния. «Что интересного вы заметили?» Для того. затем детям вводятся как можно найти стоимость покупки зная цену и кол-во товара а также как находится цена 1 товара или кол-во предметов. Затем учитель предлагает шк. фиксировать условие и требование к задаче виде таблицы. Затем пропорциональность распространяется на другие величины.
23. Аксиоматическое построение мн-ва натур-х чисел. N числами называются элементы множества М, для которого установлено отношение «непосредственно следовать за», удовлетворяющее следующим аксиомам: А1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей. А2. Для каждого элемента а из N существует единственный элемент а', непосредственно следующий за а. А3. Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а. А4. Если множество М есть подмножество N и а) единица содержится в М; б) из того, что а содержится в М, следует, что и а' содержится в М, то множество М совпадает с множеством N. Если в качестве множества N выбрать некоторое конкретное множество, на котором задано конкретное отношение «непосредственно следовать за», удовлетворяющее аксиомам 1—4, получим различные интерпретации (модели) данной системы аксиом. Сложением N чисел называется алгебраическая операция, определенная на множестве N натуральных чисел и обладающая св-ми: 1)
20. Методика изучения нумерации многозначных чисел. Изучение нумерации многозначных чисел связано с необходимостью усвоить разряды и классы, а также ряд понятий, связанных с ними. Умение записать число в виде суммы слагаемых, умение назвать общее количество единиц разряда, класса и т.д. вырабатываются после длительных и повторных упражнений. Чтобы безошибочно читать и записывать многозначное число, ученик должен практически овладеть структурой таких чисел (разрядные слагаемые). Изучение многозначных чисел следует связать с именованными числами, с краеведческим материалом, с конкретными примерами из жизни, с личным опытом учащихся. Нумерация многозначных чисел изучается в 3 классе: сначала изучают четырехзначные числа, затем пятизначные, наконец, шестизначные числа; после этого им дается понятие о разряде и классе. Изучение нумерации многозначных чисел опирается на знания учеников о нумерации чисел в пределах 1000. Схема разбора многозначного числа: 1.Прочитать число. 2.Назвать число единиц каждого разряда и класса в отдельности. 3.Назвать высший разряд числа. 4.Назвать общее кол-во единиц каждого разряда. 5.Назвать предшествующее и последующее числа по отнош к данному. 6.Назвать наим и наиб числа, составленные из такого же кол-ва разрядов. 7.Назвать наим и наиб числа, записанные всеми цифрами данного числа. 8.Записать данные числа, как сумму разрядных слагаемых.
24. Письменные приемы сложения и вычитания являются основными вычислительными действиями при вычислениях в объеме многозначных чисел, поскольку вычисление в уме с многозначными числами слишком сложная проблема для всех детей. При знакомстве с письменными приемами сложения и вычитания многозначных чисел производится аналогия с алгоритмом письменного сложения и вычитания в пределах 1000: 1. письменное сложение и вычитание любых многозначных чисел выполняется также как сложение и вычитание трехзначных чисел. 2. при записи столбиком, как и при сложении трехзначных чисел следует записывать разряд под соответствующим разрядом, и складывать сначала единицы, потом десятки, потом сотни, а потом тысячи (справа-налево). Наиболее сложными являются случаи требующие "заёма" разрядных единиц не из соседних, а из далеко стоящих разрядов. Эти случаи полезно сопровождать подробной записью на доске, чтобы дети понимали и владели откуда появляется 9ки в "пустых" разрядах. Сложение и вычитание многозначных чисел изучается одновременно. Подготовительная работа к изучению темы начинается еще при изучении нумерации многозначных чисел: повторяют устные приемы сложения и вычитания и свойства действия, на которые они опираются, повторяют письменные приемы сложения и вычитания трехзначных чисел, сложения и вычитания разрядных чисел с пояснениями (6 сот. + 7 сот.=13 сот. и это = 1 тыс. 3 сот.). Вслед за изучением + и - многозначных чисел приступают к сложению и вычитанию составных именованных чисел, выраженных в метрических мерах, так как приемы этих вычислений сходны. Можно перевести всё в одну меру, а можно по отдельности складывать сходные меры.
25. Определение суммы через объединение множеств. Суммой целых неотрицательных чисел 𝖆 и b называют число элементов в объединении непересекающихся множеств А и В, что n (А) = 𝖆, n (В)= b: 𝖆 + b= n (А∪В), где n (А) = 𝖆, n (В)= b и А∩В = Заметим, что равенство n( А∪В) = n (А)+ n (В) перестает быть верным, если множества А и В имеют общие элементы. Пусть например, А= {a,b,c,d,e}, В={d,e,f,g }. Тогда А∪В = {a,b,c,d,e, f,g }. Видим, что множество А состоит из 5 элементов, множество В из 4 элементов, но множество А∪В состоит не из 5+4=9 элементов, а из 7 элементов, т.к. элементы d и e входят в оба множества А и В, а при объединении они считаются лишь один раз. Поэтому для получения числа элементов в А∪В надо из 5+4 =9 вычесть 2, т.е. число элементов в пересечении множеств А и В. Таким же образом доказывается, что верна формула: n( А∪В)= n (А)+ n (В) – n(А∩В). Связь вычитания со сложением устанавливается при рассмотрении темы «Как найти неизвестное слагаемое». Правила вычитания из суммы и суммы из числа вводятся по существу на теоретико- множественной основе.
26. Алгебраический материал - это уравнение и выражение. В начальном курсе матем предусматривается постепенная подготовка учащихся к усвоению понятия переменной (сам этот термин не используется). Числ. выраж - это выражение, кот содержит числа, знаки действий, скобки. А если содержит ещё буквы, то это - выражение с переменной. Уравнение - это равенство с одной переменной. Решить уравнение - найти переменную, а переменная - это корень уравнения. Начинается эта работа в 1 кл, где рассматриваются так называемые примеры «с окошечком». Во 2 кл буква выступает уже в соответствующих выражениях как переменная, кот может приобретать различные числ знач. Постепенно, усложняется работа, связанная с решением уравнений. Умение решать уравнение применяется при решении текстовых задач. При формировании у детей понятия математического выражения необходимо учитывать, что знак действия, поставленный между числами, имеет двоякий смысл: с одной стороны, он обозначает действие, которое надо выполнить над числами (6+4 - к 6ти прибавить 4). С другой стороны знак действия служит для обозначения выражения (6+4 - это сумма чисел 6ти и четырех). Понятие о выражении формируется у младших школьников в тесной связи с понятиями об арифметических действиях и способствует лучшему их усвоению. 2 этапа работы над выражениями: 1. Понятие о простейших выражениях (сумма, разность, произведение). 2. Сложные выражения (сумма произведения и числа, разность двух частных и т.д.). 2 подхода выполнения действий: 1. сначала в скобках, потом за ними. 2. Действие первого порядка - умножение, деление действие второго порядка - сложение, вычитания.
27. Высказывание B(x) следует из высказывания A(x), если B(x) обращается в И высказ при всех тех значениях, при которых A(х) – И. Знак «==> - это знак отнош следования между предложениями. Если из предлож А следует В, а из предлож В след А, то говорят, что предлож А и В равносильны. A(x) – достаточно для B(x), а B(x) – необходимо для A(x). Теоремы: A=>B (прям); B=>A (обрат); A=>B (против); B=>A (обрат-против). Теорема – высказ, истинность которого устанавливается посредством рассуждения (А – условие, В-заключение). Доказать теорему А=>В- это значит установить логическим путем, что всегда, когда выполняется свойство А, будет выполняться и свойство В. В основе доказательства лежит рассуждение - логическая операция, в результате которой из одного или нескольких взаимосвязанных по смыслу предложений получается предложение, содержащее новое (по отношению к исходным) знание. Рассуждение, между посылками и заключением которого имеет место отношение следования, назыв. дедуктивным. Метод индукции- на основании ряда частных случаев делается общий вывод. Это такое рассуждение, при котором на основании того, что некоторые объекты совокупности обладают определенным свойством, делается вывод о том, что этим свойством обладают все объекты этой совокупности.
28. Цели геометр материала состоят в формир у детей представлений о геометр фигурах различных видов (точки, прямой и кривой линиях, отрезки ломаной , различных видов многоуголв, круге, окружности.) дети должны научиться узнавать, различать и изображать эти фигуры. При ознакомлении с геометр материалом значит место уделяется измерениям: дети должны научиться находить длину отрезка(1 кл), длину ломаной, периметр данного многоугольника (2 кл), площадь прямоугольника (3 кл). При этом определения понятий детям не сообщаются (и соответственно от учащихся не требуется их знания). Различать классы фигур, относящихся к ближайшему родовому понятию (прямоугольник- 4угольник, у кот все углы прямые, квадрат- прямоугольник, у кот все стороны равны и т.п). Дети должны научиться фактически использовать соответствующие признаки при узнавании различных фигур. На практике геометрия применяется при вычерчивании фигур. 1 кл.- научиться пользоваться линейкой, построение на клетчатой бумаге прямоугольника(квадрата).2 кл.- дети должны уметь пользоваться циркулем для вычерчивания окружностей. 3 кл.- научиться строить прямой угол и прямоугольники на не линованной бумаге с помощью чертежного угольника. В матем нач школы в основном рассматр плоскостные фигуры (квадрат, круг, прямоугольник). Начальные геометр понятия (линии, простейшие геом. фигуры и тела, симметрия, простейшие планы и т.д.) изучаются в1 и 2 кл совместно с изучением арифметики. В 3 и 4 кл геометрия изучается на отдельных уроках.
29. Величины, кот выражают одно и тоже св-во, назыв величинами одного рода или одной величины. Для любых А и В однозначно определяется величина С=А+В, которой называют суммой величин А и В сложение коммутат и ассоциат. Величины одного рода можно вычитать. Определяют вычитание через сложение. Разность А и В наз-ся такая величина С=А-В, что А=В+С. Разность сущ-ет тогда, когда А меньше В. Величину можно умножать на полож действ число. Для любого А и для любого действ числа Х сущ-ет ед-ая величина В=Х*А – произведение величин А на число Х. Величины одного рода можно делить, получая рез-т число. Деление определяют через умножение. Частным величин А и В называют полож. действ число х=А:В, что А=Х*В. Число х наз-ся численным значением величины А при ед-це величины Е. Оно показывает, во сколько раз величина А больше/меньше величин Е. Если А=х*Е, то число х называют также мерой величины А при ед-це Е и пишут х=mе(А). Скалярная величина – величина которая опр-ся одним численным значением. Полож скалярная велич - если скалярная величина принимает только полож численные значение. Если величины выражают разные св-ва обьекта, то их называют разнородные величины, н-р длина и масса разн велич. Смысл натур числа, получ в рез-те измен величин. Сумма отрезков. Считают, что отрезок х сост из отрезков Х1 …..,если он яв-ся обьедин и никакие два из них не имеют общих внутр точек, хотя и могут иметь общие концы. Если отрезок х сост из а отрезков, каждый из которых = единич отрезку L, то число а назыв численным значением длины х данного отрезка при единице длины Е. Отсюда следует, что N число как рез-т измерения длины отрезка показ-ет, из скольки единич отрезков сост отрезок, длина которого измер.
30. Текстовая задача – описание некоторых ситуаций на естеств языке с требованием дать коллич хар-ку какого-либо компонента этой ситуации. 2 части: условие – непосред ситуация (данное); требование – указание того, что нужно найти (искомое). Методы решения: арифмет (действия), алгебр (уравнения), логич (рассужд, граф, таблицы), геометрич (рисунок), практич. Почти половина времени на уроках математики отводится решению задач. Решение арифметических задач помогает раскрыть основной смысл арифметических действий, конкретизировать их, связать с определенной жизненной ситуацией. Этапы работы над задачей:1) работа над содержанием;2) поиск решения;3) решение;4) формулировка ответа;5) проверка решения;6) последующая работа над решенной задачей. Работа над решенной задачей. а)изменение условий задачи так чтобы в задачи решалась др.действием. б)постановка нового вопроса к уже решенной задаче. в)постановка всех вопросов ответы е-е можно дать. г)сравнение содерж. решения одной задачи с содерж. др. задачи. д)Решение задачи одним способом или др. е)изменение числ. данных так чтобы появился новый способ решения или чтобы задача не имела решения. ж)сполько способов решения имеет решение. При каких условиях она бы не имела решения? какие приемы целесообразны наиболее для решен. этой задачи возможными др. методы решения. Простые задачи (1 действие): 1. на нахождение суммы. 2. на нахождение разности. 3. на разностное сравнение. 4. на кратное сравнение (результат деления, при котором узнаем во сколько раз одно число больше или меньше другого). Задачи по классам: модель (символ, естеств), график, чертеж, графич (рисунок, схема), граф, таблица, вербальная модель, предметная модель.
31. Функция – одно из важнейших понятий матем. В шк. курсе основное внимание уделяется числ функциям. Числ функция– такое соответствие м\у числ множ Х и множ R действ. чисел, при кот каждому числу из множ Х сопоставляется единственное число из множ R. Все значения, кот принимает аргумент - область определения. Все значения? кот принимает функция при x ϵ D(f) – область значения. Задать функцию – указать правило, по кот произвольно выбранному значению x ϵ D(f) можно вычислить значение у. Способы задания функции: аналитический (формула), табличный, графический (график), словесный. Линейная- функция вида: y = kx+ b; где k ϵ R, b ϵ R. График – прямая. При b = const – графики проходят через точку (0;b); при а = const – сдвиг функции на а ↑или↓. Квадратичная- функция вида: y = ax2 + bx + c; где a, b, c ϵ R, a≠0. График – парабола. a>0 –ветви вверх, a<0 – вниз. D > 0 – 2 корня, D = 0 – 1 корень, D < 0 – корней нет. Частный случай- функция вида: y = x2. График – парабола. Функция вида a(x+m0) + n0: m0 – сдвиг по оси ОХ, n0 – сдвиг по оси ОУ, где (m;n) - точки вершины.
32. Нумерация чисел 1-10, значение придаётся вопросом, связанным с получением каждого нового числа, с выяснением соотношений, существующих между смежными числами ряда, с рассмотрением состава чисел из 2-х слагаемых. Большое внимание уделяется работе, направленной на подготовку детей к изучению действий сложения и вычитания. При рассмотрении каждого из чисел, прежде всего должно быть выяснено, как оно может быть получено. Для того чтобы подчеркнуть принцип построения натурального ряда чисел, важно начать с получения числа путём прибавления единицы к предыдущему числу. Получение числа прибавлением единицы к предыдущему или вычитанием единицы из последующего легко связать со сравнением этих чисел. Каждое новое число с самого начала выступает как продолжение изученного отрезка натурального ряда чисел. При таком подходе создаются условия для того, чтобы дети подметили некоторые общие св-ва чисел натурального ряда: не только данное рассматриваемое на этом уроке число, но и вообще любое число может быть получено прибавлением 1 к тому числу, которое встречается при счёте перед ним, или вычитанием 1 из числа, которое идёт при счёте сразу же после него. Чтобы у детей не сложилось такого впечатления, что числа образуются только с помощью прибавления или вычитания единицы, очень важно показать им различные способы получения чисел из 2-х и более слагаемых. На уроках, посвещённых числам 1-5, надо выполнить довольно много упр., направленных на прочное усвоение состава этих чисел. При рассмотрении чисел 6-10 такие упражнения должны выполняться лишь эпизодически, чтобы дети понимали, что и эти числа можно заменять суммой двух каких-то других меньших чисел. Важна наглядность, демонстрация. При изучении каждого из чисел повторяется не только умение считать предметы, но и определять порядковый номер. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
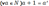 2)(
2)(  . Сложение N чисел коммутативно и ассоциативно. Умножением N чисел называется алгебраическая операция, определенная на множестве N натуральных чисел и обитающая св-ми: 1) (
. Сложение N чисел коммутативно и ассоциативно. Умножением N чисел называется алгебраическая операция, определенная на множестве N натуральных чисел и обитающая св-ми: 1) ( 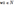 ) а • 1 = а; 2) (
) а • 1 = а; 2) ( 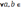 N)a·b= ab+ а. Умножение N чисел коммутативно, ассоциативно и дистрибутивно относительно сложения. Разностью N чисел а и bназывается N число с = а — b, удовлетворяющее условию: b + с =а. Частным N чисел а и bназывается N число с=a:b, удовлетворяющее условию: b • с = а.
N)a·b= ab+ а. Умножение N чисел коммутативно, ассоциативно и дистрибутивно относительно сложения. Разностью N чисел а и bназывается N число с = а — b, удовлетворяющее условию: b + с =а. Частным N чисел а и bназывается N число с=a:b, удовлетворяющее условию: b • с = а. . Сумма целых неотрицательных чисел всегда существует и единственна, т. е. у любых двух целых неотрицательных чисел 𝖆 и b можно найти их сумму – целое неотрицательное число 𝖆 и b. Существование и единственность суммы вытекают из существования и единственности объединения двух множеств. Определение. Разностью натур чисел a и b называется натуральное число с = a – b, удовлетворяющее условию b+с = a. Законы сложения. Коммуникативность: для любых множеств А и В выполняется равенство А∪В= В∪А. Если 𝖆 =n (А), b=n (В) и А∩В =
. Сумма целых неотрицательных чисел всегда существует и единственна, т. е. у любых двух целых неотрицательных чисел 𝖆 и b можно найти их сумму – целое неотрицательное число 𝖆 и b. Существование и единственность суммы вытекают из существования и единственности объединения двух множеств. Определение. Разностью натур чисел a и b называется натуральное число с = a – b, удовлетворяющее условию b+с = a. Законы сложения. Коммуникативность: для любых множеств А и В выполняется равенство А∪В= В∪А. Если 𝖆 =n (А), b=n (В) и А∩В =  , то 𝖆 + b= n( А∪В) = n(В∪А)= b +𝖆. Ассоциативность (сочетат) вытекает из равенства: ( А∪В) ∪С = А∪(В∪С).
, то 𝖆 + b= n( А∪В) = n(В∪А)= b +𝖆. Ассоциативность (сочетат) вытекает из равенства: ( А∪В) ∪С = А∪(В∪С).