
|
|
Экзаменационный билет № 3Экзаменационный билет № 1 Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти наверняка. Лемма Маркова гласит [6]: если случайная величина Х не принимает отрицательных значений, то для любого положительного числа α справедливо следующее неравенство: Д о к а з а т ь е л ь с т в о. Проведем доказательство для дискретной случайной величины способом, получившим название метода урезания. Пусть | x1|, | x2 |, ..., | xn | - есть упорядоченная совокупность всех значений случайной величины x , с соответствующими вероятностными pi = P{| x | = | xi | }, причем å pi = 1. Не нарушая общности доказательства, можно допустить, что абсолютные значения случайной величины x расположены в порядке убывания. Выберем произвольное e >0 и предположим, что первые r значений совокупности не меньше e (r £ n) . Запишем следующее неравенство: | x1 | p1 + | x2 | p2 + ... + | xr | pr £ | x1 | p1 + ... + | xr | pr + ... + | xn | pn = M | x | . Следовательно, Заменяя в левой части последнего неравенства значение |xi| числом e , получим усиленное неравенство: e × Левая часть выражает вероятность того, что модуль случайной величины принимает значение, не меньшее e , т.е.
Основные задачи теории выборки При применении выборочного наблюдения возникают три основные задачи: • определение объема выборки, необходимого для получения требуемой точности результатовс заданной вероятностью; • определение возможного предела ошибки репрезентативности, гарантированного с заданнойвероятностью, и сравнение его с величиной допустимой погрешности. • определение вероятности того, что Ошибка выборки не превысит допустимой погрешности. Все эти задачи решаются на основе теоремы Чебышева, согласно которой Р {[ х - ? | < ε } ≥ 1 -h, когда п - достаточно большое число; ε и h — сколь угодно малые положительные числа. Экзаменационный билет № 2 Неравенство Чебышева Нера́венство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего. Неравенство Чебышёва является следствием неравенства Маркова. Пусть случайная величина
где Если
В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на
Проблемы статистических выводов традиционно делятся на проблемы оценивания и проверку гипотез. Главное различие между этими двумя проблемами состоит в том, что при оценивании мы должны определить величину параметра или нескольких параметров. В то время как при проверке гипотез мы должны решить: принять или отвергнуть специфическую величину (или ряд специфических величин) параметра или нескольких параметров. В общем виде задача оценки параметров формулируется следующим образом. Пусть распределение признака Х - генеральной совокупности - задается функцией вероятности f(x, θ) = P(X=xi) для дискретной случайной величины или плотностью вероятностей для непрерывной случайной величины, которая содержит неизвестный параметр θ. Для вычисления параметра θ используют выборку x1, x2, ..., xn, каждая из которых имеет один и тот же закон распределения, что и признак Х. Оценкой θn параметра θ называют всякую функцию результатов наблюдений (иначе - статистику), с помощью которой делают вывод о значении параметра θ: θn = θn(x1, x2, ..., xn). Так как x1, x2, ..., xn - случайные величины, то и оценка θn является случайной величиной, которая зависит от закона распределения и объема выборки n. Оцениваемый параметр θ является постоянной величиной. Всегда существует множество функций от результатов наблюдений x1, x2, ...xn, которые можно предложить в качестве оценки параметра θ. Например, для математического ожидания в качестве оценки θn по выборке можно взять среднюю арифметическую результатов наблюдений Какими свойствами должна обладать оценка θn? Так как θn - случайная величина, то невозможно предсказать индивидуальное значение оценки в данном частном случае. Поэтому о качестве оценки следует судить не по ее индивидуальным значениям, а по распределению ее значений при достаточно большом числе испытаний, т. е. по выборочному распределению оценки. Экзаменационный билет № 3 Теорема Чебышева Теорема. Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное числоe, вероятность неравенства будет сколь угодно близка к единице, если число случайных величин достаточно велико. Т.е. можно записать: Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается: Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины. Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий. Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются. Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности. Оценки подразделяются на два класса; точечные и интервальные. Точечные оценки представляют собой определенные значения параметров генеральной совокупности, полученные по выборочным данным. Эти значения должны быть максимально близки к значениям соответствующих параметров генеральной совокупности, которые являются истинными значениями оцениваемых параметров. При формировании интервальных оценок определяют границы интервалов, между которыми с большой вероятностью находятся истинные значения параметров. Начнем с точечных оценок и рассмотрим оценку произвольного параметра (среднего, дисперсии или какого-то другого) генеральной совокупности, который обозначим a. Оценивая параметр a по выборке, находим такую величину aВ, которую принимаем за точечную оценку параметра a. Естественно, при этом стремимся, чтобы оценка была в определенном смысле наилучшей, поэтому к ней предъявляется ряд требований: 1. Состоятельность. Точечная оценка aВ называется состоятельной, если при неограниченном увеличении объема выборки ( В математической статистике показывается, что состоятельной оценкой генерального среднего значения 2. Несмещенность. Оценка aВ называется несмещенной, если она не содержит систематической ошибки, т. е. среднее значение оценки, определенное по многократно повторенной выборке объема n из одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра a. Выборочное среднее арифметическое Несмещенной оценкой генеральной дисперсии 3. Эффективность. Несмещенная оценка является эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещенными оценками того же параметра генеральной совокупности. Это надо понимать так: полученные по выборке оценки Итак, наилучшими в указанном смысле оценками генерального среднего значения и генеральной дисперсии являются выборочные характеристики 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 pi £ M | x | или
pi £ M | x | или 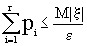 .
. . n
. n определена на вероятностном пространстве
определена на вероятностном пространстве  , и еёматематическое ожидание
, и еёматематическое ожидание  и дисперсия
и дисперсия  конечны. Тогда
конечны. Тогда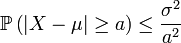 ,
, .
. , где
, где 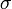 - стандартное отклонение и
- стандартное отклонение и 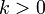 , то получаем
, то получаем .
. стандартных отклонения с вероятностью меньше
стандартных отклонения с вероятностью меньше  . Она отклоняется от среднего на
. Она отклоняется от среднего на  стандартных отклонения с вероятностью меньше
стандартных отклонения с вероятностью меньше  .
.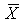 , моду M0, медиану Me и т. д.
, моду M0, медиану Me и т. д. ) она стремится к истинному значению параметра a.
) она стремится к истинному значению параметра a.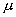 , является выборочное среднее арифметическое
, является выборочное среднее арифметическое  , а состоятельной оценкой генеральной дисперсии
, а состоятельной оценкой генеральной дисперсии  — выборочная дисперсия
— выборочная дисперсия  . Методы вычисления этих выборочных характеристик были рассмотрены в гл. 3.
. Методы вычисления этих выборочных характеристик были рассмотрены в гл. 3.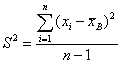 для несгруппированных данных,
для несгруппированных данных, для сгруппированных данных,
для сгруппированных данных,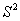 .
.