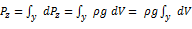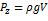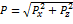|
|
Сила давления жидкости на плоские и криволинейные стенки.Дифференциальные уравнения равновесия жидкостей (Эйлера).
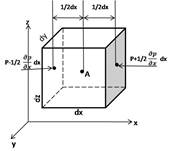
dP’x=(p-1/2 dP’’x=( P+1/2 dM=dmj=ρdVj=ρdxdydzj; dP’x-dP’’x+dM=0 (p-1/2 Pdydz-1/2 Ур-ие Эйлера Из этих уравнений видно, что гидростатистическое приращение давления в направлении какой-либо координатной оси возможно только при наличии ускорения в направлении этой же оси и происходит за счет массовых сил: Дифф. Ур-ие равновесия жид-тей (Эйлера) Выражает функциональную зависимость давления от рода жидкости и координат точки в пространстве и позволяет определить значение давления в любой точке жидкости. Уравнение поверхности, равного давлению. P=const, dp=0 Xdx+Ydy+Zdz=0 1 случай.Жид-ть нах-ся в равновесии в резервуаре в поле действия только силы тяжести. В этом случае проекции результирующей еденичных массовых сил будут след: X=0, Y=0, Z= -g. Подставляя данные значения в уравнение поверхности равного давления получим: -gdz=0, или после интегрирования: gz=const. Это уравнение горизонтальной плоскости. Следовательно, в покоящейся жидеости любая горизонтальная плоскость явл-ся плоскостью равного давления. Случай.
Или после интегрирования: ax+gz=const. Это уравнение наклонной плоскости. Угол наклона к горизонту β=arctg (a/g)
Случай.
X=
Это уравнение парабалоида вращения. Пов-ти равного давления представляют собой семейство парабалоидов вращения , расположенных вокруг вертик.оси.
dp= dp= - dp= - после интерирования получаем: p= - Для определения пост. Интегрирования задаемся начальными условиями. Точка А на свобод.поверхности жидкости Z=z0 p=p0; P0= -
Основное уравнение гидростатики выражает зависимость точки покоящейся жидкости от рода жидкости и расстояния точки от своболной поверхности. р- абсолют. Давление в данной точке жидкости ,р0- давление окруж.среды Монометрическое и вакуум.давление в открытых сосудах и водоемах Р=ра+ Закон Паскаля- абсолют. Давления в точках жидкости,находящиеся на разн.глубинах будут различны,однако внешнее давление на жидкость,заключ. В замкнутом сосуде передается всем ее частицам без изменения.
p1= Cообщающиеся сосуды P=p1+ P=p2+
Сила давления жидкости на плоские и криволинейные стенки.
Для такой бесконечно малой площади давление во всех ее точках одинаково и равно: · Сила давления жидкости на элементарную площадку:
· Cила давления на всю рассматриваемую площадь F:
Следовательно
Сила давления на плоскую стенку равна произведению смоченной жидкостью площади фигуры на гидростатическое давление на ее центр тяжести:
Если на свободную поверхность действует давления, отличные от атмосферного, силу давления на стенку можно найти по формулам:
Где ,
Центр давления лежит всегда ниже центра тяжести. В соответствии с теоремой Вариньона о моменте равнодействующей(момент равнодействующей силы относительно какой-либо оси равен сумме моментов соответствующих сил относительно той же оси)
Заменив в последнем выражении Р и dP их значениями, получим:
Момент инерции относительно оси Х , который может быть выражен через момент инерции относительно центральной оси, параллельной оси Х
Центр давоения жидкости совпадает с центром тяжести в случае когда мы рассматриваем горизонтальное дно: Гидростатический парадокс.
Сила давления жидкости на криволинейную стенку.Тело давления.
Сила давления на элементарную площадку:
· Горизонтальная : · Вертикальная: Тогда их проекции:
Результирующая сила давления:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 P-1/2
P-1/2 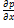 dx , P+1/2
dx , P+1/2  dx)dydz;
dx)dydz;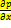 = ρX;
= ρX;  = ρY;
= ρY;  = ρZ
= ρZ dy= ρYdy;
dy= ρYdy;  dz= ρZdz; X,Y,Z –ускорения
dz= ρZdz; X,Y,Z –ускорения В этом случае любая частица жид-ти нах-ся под действием ускорений а и g, следовательно проекции результирующей еденичных массовых сил будут след: X=-a; Y=0; Z=-g; -adx-gdz=0;
В этом случае любая частица жид-ти нах-ся под действием ускорений а и g, следовательно проекции результирующей еденичных массовых сил будут след: X=-a; Y=0; Z=-g; -adx-gdz=0;
 x;
x;  =
=  y; Z=-g.
y; Z=-g.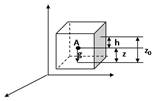 Основное уравнение гидростатики
Основное уравнение гидростатики (xdx+ydy+zdz)
(xdx+ydy+zdz)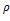 zdz
zdz +p0+
+p0+ 
 - избыточное давление или давление столба жидкости в данной точке.
- избыточное давление или давление столба жидкости в данной точке. атмосф.
атмосф. 
 ра -
ра - 
 Р1 Р2
Р1 Р2


 d1 d2
d1 d2 
 p2=
p2= 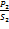
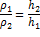
 C-центр тяжести, D –центр давления
C-центр тяжести, D –центр давления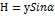
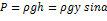
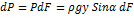
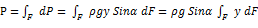
 – статический момент
– статический момент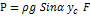

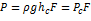
 - это расстояние от центра тяжести рассматриваемой площадки до свободной поверхности.
- это расстояние от центра тяжести рассматриваемой площадки до свободной поверхности.

 – вакууметрическое давление
– вакууметрическое давление - манометрическое давление
- манометрическое давление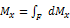




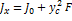
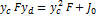
 - от центра давления до свободной поверхности.
- от центра давления до свободной поверхности.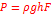
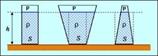 Из этого рисунка видно, что различной формы сосуды, имеющие одинаковые площади доньев и заполненные одинаковой жидкостью на одну и ту же высоту, будут иметь одинаковую силу давления на дно не зависимо от формы сосуда и количества находящейся в нем жидкости.(гидростатический парадокс) D=C
Из этого рисунка видно, что различной формы сосуды, имеющие одинаковые площади доньев и заполненные одинаковой жидкостью на одну и ту же высоту, будут иметь одинаковую силу давления на дно не зависимо от формы сосуда и количества находящейся в нем жидкости.(гидростатический парадокс) D=C
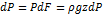
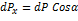
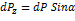
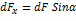
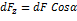
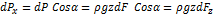
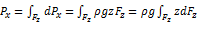
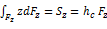
 - это статический момент площади вертикальной проекции криволинейной стенки относитеьлно
- это статический момент площади вертикальной проекции криволинейной стенки относитеьлно  , проходящей по свободной поверхноси жидкости.
, проходящей по свободной поверхноси жидкости. - это площадь вертикальной проекции криволинейной стенки, смоченной жидкостью.
- это площадь вертикальной проекции криволинейной стенки, смоченной жидкостью.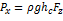
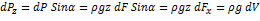
 - элементарный объем жидкости
- элементарный объем жидкости