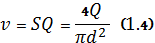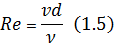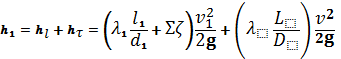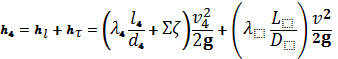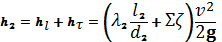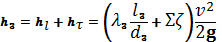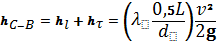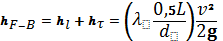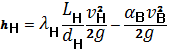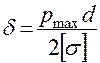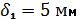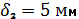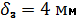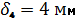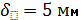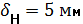|
|
Схема водозабора раздельного типаРОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ и ГАЗА Им. И.М. Губкина Факультет разработки нефтяных и газовых месторождений
Кафедра нефтегазовой и подземной гидромеханики
Курсовая работа по курсу «Гидравлика»
«Гидравлический расчет водозабора раздельного типа системы заводнения пласта с заданными диаметрами водозаборных труб»
К защите: научный руководитель ______________
студент группы ______________
Защита: Председатель комиссии _____________
Член комиссии _____________
Оценка
Москва
Содержание Введение 3 Теоретическая часть 4 Задание на курсовую работу 6 Расчетная часть 8 ü Определение расхода воды во всасывающей трубе насоса по заданным диаметрам подводящих труб и допустимой высоте всасывания. ü Определение минимально-необходимой толщины стенки. Заключение 15 6.Список используемой литературы 16 Введение. Сложный трубопровод имеет разветвлённые участки, состоящие из нескольких труб (ветвей), между которыми распределяется жидкость, поступающая в трубопровод из питателей. Сечения трубопровода, в которых смыкаются несколько ветвей, называются узлами. В зависимости от структуры разветвлённых участков различают следующие типы сложных трубопроводов: с параллельными ветвями; с концевой раздачей жидкости; с непрерывной раздачей жидкости; с кольцевыми участками. В практике встречаются разнообразные сложные трубопроводы комбинированного типа. Можно выделить три основные группы задач расчёта сложных трубопроводов: 1) Определение размеров труб по заданным в них расходам и перепадам напоров в питателях и приёмниках. 2) Определение перепадов напоров в питателях и приёмниках, необходимых для обеспечения требуемых расходов в трубах заданных размеров. 3) Определение расходов в трубах заданных размеров по известным перепадам. В данном курсовом проекте рассматривается третья из представленных групп задач. По существу это поверочный расчёт уже существующего трубопровода, выясняющий условия его работы. Безусловно, знание расходов в трубах на промысле просто необходимо. Теоретическая часть. Для решения сформулированных выше задач составляется система уравнений, устанавливающая связи между размерами труб, расходами жидкости, напорами. Эта система состоит из уравнений баланса расходов для каждого узла и уравнений Бернулли для каждой ветви трубопровода. При этом в сложных трубопроводах можно пренебрегать относительно малыми местными потерями напора в узлах. Это позволяет считать одинаковыми напоры потоков в концевых сечениях труб, примыкающих к данному узлу, и оперировать в уравнениях Бернулли понятием напора в данном узле. Уравнение Бернулли для участка трубопровода 1-2 записывается в виде
где z – геометрический напор;
В данной курсовой работе участки, для которых записываются уравнения Бернулли, на всём протяжении имеют постоянный диаметр, поэтому
Потери напора в трубах выражаются формулой Дарси – Вейсбаха (см.[2] стр. 103)
где
Поскольку средняя скорость потока в трубе выражается формулой
где а местными сопротивлениями пренебрегаем, то потери напора можно написать в следующем виде
Коэффициент сопротивления трения
В зоне гидравлически гладких труб (
В доквадратичной области турбулентного режима для шероховатых труб (
В квадратичной области вполне шероховатых труб (
Т.о, используя формулы (2), (5) – (8), можно получить зависимости типа
для каждого участка трубопровода. Используя тот факт, что Задание на курсовую работу Схема водозабора раздельного типа
Насос, Соединение труб, Фильтр. Гидравлический расчет водозабора раздельного типа системы заводнения пласта с заданными диаметрами водозаборных труб: 1. Определение расхода воды во всасывающей трубе насоса по заданным диаметрам подводящих труб и допустимой высоте всасывания. 2. Расчет толщины стенки труб
Расчетная часть. Примем m=1,13*10-3 кг/(м∙с)
1) Выберем сечения 3-3 на поверхности жидкости водоема и сечение трубопровода перед насосом В-В. Для этих сечений запишем уравнение Бернулли.
Разность Давление на поверхности равно атмосферному – РАТМ. Давление на входе в насос, равно давлению насыщенных паров. РНП. Скорость движения жидкости на поверхности питателя равна нулю. В результате получим следующее уравнение:
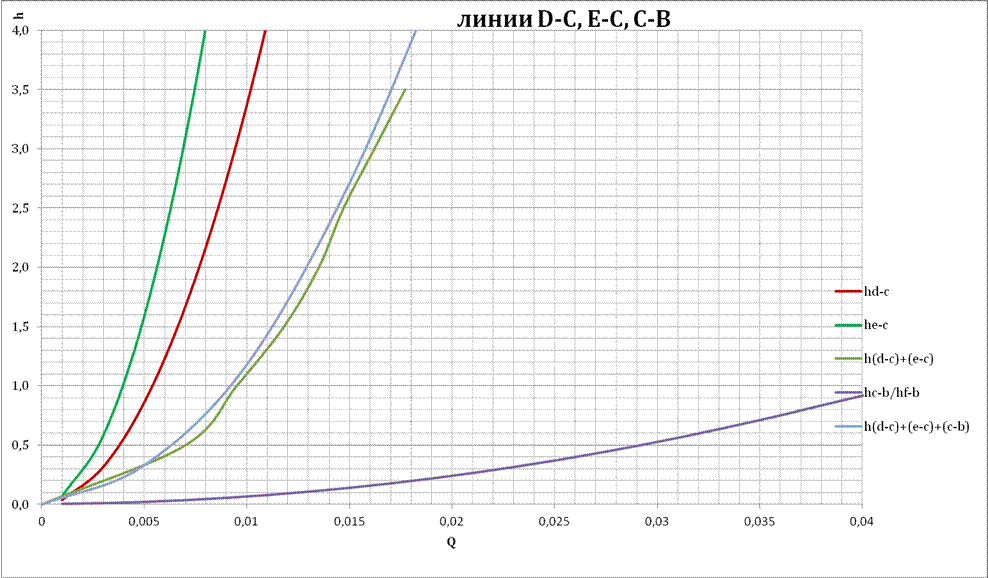
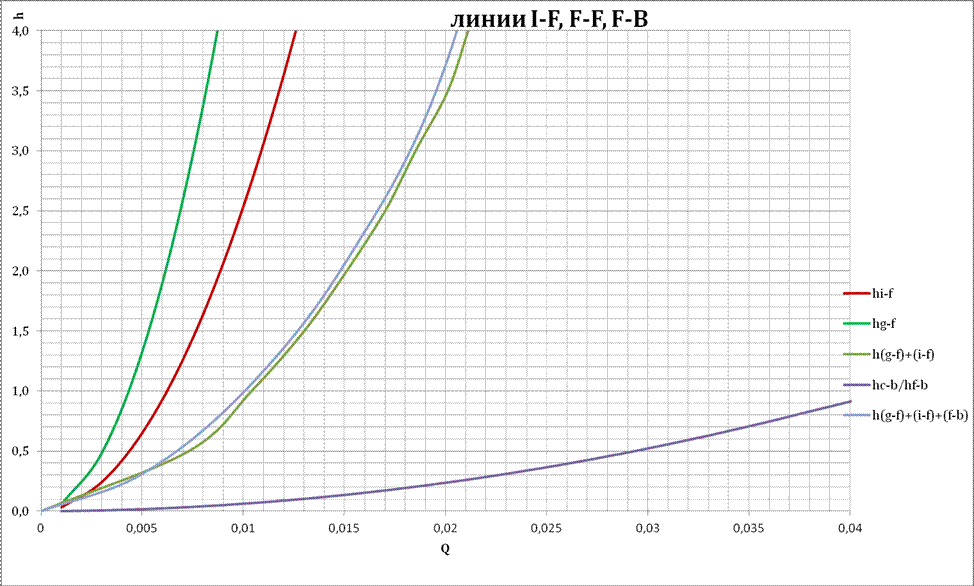
Для расчета суммарных потерь на трение системы воспользуемся графоаналитическим методом, рассчитывая участки D-C и E-C, соединённые параллельно, G-F и I-F, соединённые параллельно, С-B, F-B, B-A, по уравнению Бернулли.
В данной курсовой работе участки, для которых записываются уравнения Бернулли, на всём протяжении имеют постоянный диаметр, поэтому Тогда (1) примет вид
2) Для всех трубопроводов зададим произвольные значения расхода нефти Q1, Q2, Q3, Q4. QН . 3) Посчитаем значения скоростей нефти в трубах по формуле
где S – площадь живого сечения трубопровода (м2) 4) Подсчитаем значения числа Рейнольдса
5) По значению числа Рейнольдса определяем режим течения и выберем соответствующую формулу для вычисления коэффициента гидравлического сопротивления λ (Принимаем величину абсолютной шероховатости трубопроводаΔ=1 мм (согласно исходных данных) 6) Вычислим потери напора по формуле
для каждого трубопровода: для трубопровода D-C: для трубопровода I-F: для трубопровода E-C:
для трубопровода G-F:
для трубопровода C-B:
для трубопровода F-B:
для трубопровод В-А составим уравнение, учитывающее :
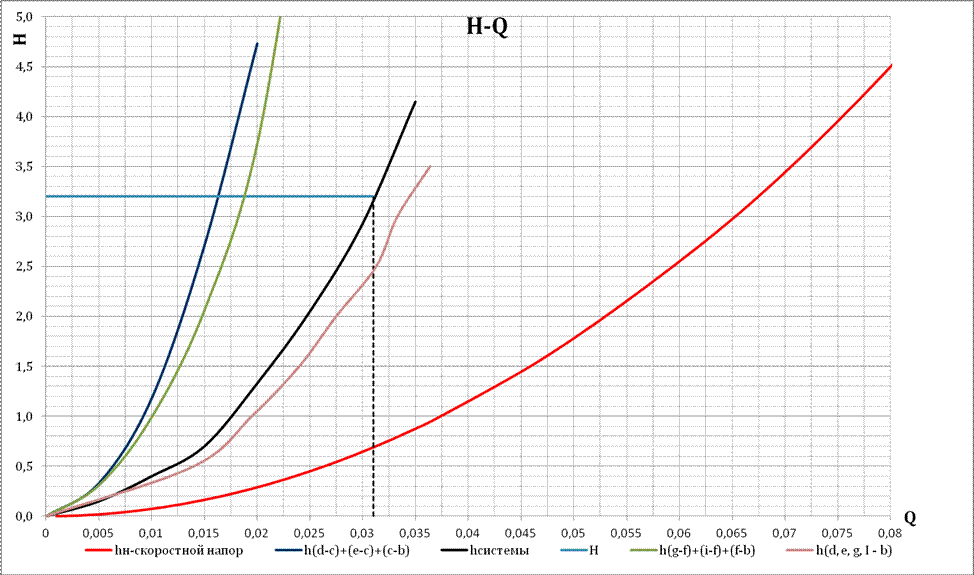
7)Построим характеристики h=f(Q) последовательно и параллельно соединенных трубопроводов и получим общую характеристику системы трубопроводов . 8)Определяем из графика №3 расход Q в системе трубопроводов по величине, найденной по формуле (2.1) Hт=3,2 м. QН =0,031 (м3/с)
График 1
График 2
График 3
11) Т.к. насос работает на всасывание, то давление в системе не может быть выше атмосферного давления откачиваемой жидкости, таким образом, для определения толщины стенки нет необходимости ее дополнительно рассчитывать по следующей формуле Примем следующие толщины стенок из стандартных типоразмеров:
Вывод. В ходе расчета работы мы получили следующие значения: Расход во всасывающей трубе насоса: QН =0,031 (м3/с) Толщины стенок трубопроводов:
В процессе выполнения работы были изучены основы графо-аналитического метода для расчета расходов воды во всасывающей трубе насоса и расходов воды в каждой водозаборной трубе исходя из диаметров и допустимой высоте всасывания. Были выбраны толщины стенок трубопроводов.
Используемая литература.
1) Г.Д.Розенберг, И.М.Астрахан, А.Е.Евгеньев, И.Н.Кочина Сборник задач по гидравлике и газодинамике для нефтяных ВУЗов, Москва 1990
2) Е.З.Рабинович, Гидравлика, Москва 1980
3) И.М.Астрахан, А.Е.Евгеньев, Г.Д.Розенберг Методические указания к выполнению курсовых работ, Москва, 1986
4) Ц.Т. Арустамова, В.Г. Иванников “Гидравлика” Москва, Недра, 1995

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1) - пьезометрический напор;
- пьезометрический напор;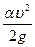 - скоростной напор;
- скоростной напор; - коэффициент Кориолиса;
- коэффициент Кориолиса; - потери напора;
- потери напора; и
и  . Кроме того, примем, что весь трубопровод лежит в одной горизонтальной плоскости, т.е.
. Кроме того, примем, что весь трубопровод лежит в одной горизонтальной плоскости, т.е.  . Тогда (1) примет вид
. Тогда (1) примет вид (2)
(2) (3);
(3);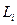 - длина трубы;
- длина трубы; - диаметр трубы;
- диаметр трубы; - коэффициент сопротивления трения;
- коэффициент сопротивления трения; - коэффициент местного сопротивления;
- коэффициент местного сопротивления; - средняя скорость потока в трубе;
- средняя скорость потока в трубе; (4);
(4); - расход жидкости в трубе;
- расход жидкости в трубе; (5);
(5); в зависимости от режима течения в трубе некоторым образом зависит от расхода Q . Так, если режим течения ламинарный (Re<
в зависимости от режима течения в трубе некоторым образом зависит от расхода Q . Так, если режим течения ламинарный (Re< 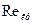 =2300 или, с учётом того, что
=2300 или, с учётом того, что  , условие перепишется так
, условие перепишется так  ), то
), то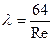 (6)
(6) или
или 
 ) – формула Блазиуса:
) – формула Блазиуса: (7)
(7) или
или  ) будем использовать приближённую формулу А.Д. Альтшуля (см.[2], стр. 140)
) будем использовать приближённую формулу А.Д. Альтшуля (см.[2], стр. 140) (8)
(8) или
или  ) формула Альтшуля переходит в формулу Б.Л. Шифринсона (см.[2], там же)
) формула Альтшуля переходит в формулу Б.Л. Шифринсона (см.[2], там же) (9)
(9) (10)
(10) (расход на участке a-b равен сумме расходов на участках b-c и b-e), а
(расход на участке a-b равен сумме расходов на участках b-c и b-e), а  ( расход на участке b-e равен сумме расходов на участках e-f и e-g), данную задачу можно решить графо-аналитическим методом.
( расход на участке b-e равен сумме расходов на участках e-f и e-g), данную задачу можно решить графо-аналитическим методом.

 =1000кг/м3, т.к. температура воды задана и равна 10о С.
=1000кг/м3, т.к. температура воды задана и равна 10о С.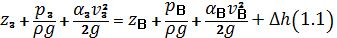
 (1.3)
(1.3)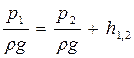 (1.3)
(1.3)