
|
|
Темы 4, 5. Статистическая обработка результатов экспериментаЦель:Ознакомить с порядком статистической обработки результатов эксперимента
План: 4.1. Необходимость обработки экспериментальных данных 4.2. Последовательность обработки экспериментальных данных
Основные понятия:среднеквадратическое отклонение результата эксперимента, доверительный интервал, доверительная вероятность В настоящее время обработка экспериментальных данных прямых многократных измеренийв нашей стране регламентируется государственным стандартом, который в общем случае предусматривает выявление закономерности поведения случайной погрешности (определения закона распределения) и статистические процедуры исключения грубых погрешностей. В практике обработки экспериментальных данных чаще всего приходится сталкиваться со случаями, когда число измерений мало (не превышает 5 - 15). В этих случаях пользуются вполне оправданным предположением о том, что закон распределения случайной погрешностиявляется нормальным (нормальный закон распределения вообще является наиболее распространенным законом распределения случайных величин, в том числе случайных погрешностей), а грубые погрешностине выявляются или определяются и отбрасываются интуитивно. Обработка экспериментальных данных прямых многократных измеренийв соответствии со стандартом базируется на теоретических положениях математической статистики, которые предполагают определение вместо характеристик нормального распределения их оценок. Так, вместо математического ожидания М[X] (является первым основным параметром нормального закона распределения), т.е. значения величины, вокруг которого группируются результаты отдельных измерений (при бесконечном числе измерений), определяется его оценка, которая представляет собой среднее арифметическое
где Xi - результат i -го измерения; n – число измерений. Второй параметр нормального закона распределения - среднеквадратическое отклонение s, характеризующее рассеяние результатов отдельных измерений относительно математического ожидания, определяется оценкой по формуле:
Оценка среднеквадратического отклонения результата измеренийопределяется по формуле:
При обработке экспериментальных данных прямых многократных измеренийпринято вычислять интервальную оценку погрешности, которая определяется с использованием погрешности S( Доверительным интервалом с границами (или доверительными границами) от - При малом числе измерений (n 20) и использовании нормального закона не представляется возможным определить доверительный интервал, так как нормальный закон распределения описывает поведение случайнойпогрешности в принципе при бесконечно большом числе измерений. Поэтому, при малом числе измеренийиспользуют распределение Стьюдента или t - распределение (предложенное английским статистиком Госсетом, публиковавшимся под псевдонимом «студент»), которое обеспечивает возможность определения доверительных интервалов при ограниченном числе измерений. Границы доверительного интервала при этом определяются по формуле
где t - коэффициент распределения Стьюдента, зависящий от задаваемой доверительной вероятности Рд и числа измерений n. Коэффициент t обычно определяется по таблице или рассчитывается по сложной формуле, описывающей распределение Стьюдента. Предполагается, что: -результаты измерений являются исправленными, т.е. из них исключены систематические погрешности; -неисключенные систематическиепогрешности настолько малы, что ими можно пренебречь; -результаты измеренийявляются равнорассеянными (равноточными) одинаково распределенными величинами (такие результаты получаются при выполнении измеренийодним оператором с помощью одних и тех же средств измерений); -из результатов измерений исключены промахи и грубые погрешности -число измерений не превосходит 15 (в этом случае признается и не проверяется нормальность распределения случайных погрешностей).
Обработка экспериментальных данных прямых однократных измерений. Ввиду того, что однократныеизмерения проводятся при условиях, когда всеми погрешностями, кроме погрешностейсредств измерений (инструментальные погрешности) можно пренебречь, результат прямого однократногоизмерения представляется в виде
где D - абсолютная погрешность для найденного значения Класс точности средства измерений- обобщенная характеристика точности средства измерений. В подавляющем большинстве случаев класс точности нормируется приведенной g или относительной d погрешностью:
или
где Xв и Xн верхний и нижний пределы измерений используемого средства измерений. Значение класса точности указывается на шкалах или корпусах измерительных устройств. При этом, если число, определяющее класс точности, заключено в окружность - ‚, то класс точности устройства следует определять по формуле (7), в противном случае - по формуле (6). Таким образом, в каждом конкретном случае для определения значения D в формуле (5) необходимо выполнить вычисления по формулам, полученным из выражений (6) и (7), соответственно:
Выводы: Обработка экспериментальных данных прямых многократных измеренийрегламентируется государственным стандартом, который в общем случае предусматривает выявление закономерности поведения случайной погрешности (определения закона распределения) и статистические процедуры исключения грубых погрешностей. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 :
: ,
,
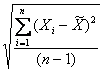 ,
,
 ) =
) =  =
= 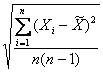 .
.
 до +
до +  ± D ,
± D ,
 ,
,
 ,
,

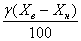 ,
,
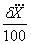 .
.