|
|
То же для случая аппроксимации ВАХ степенным полиномом третьей степени.
Для анализа прохождения сигналов через цепи, содержащие нелинейный элемент, необходимо задать его вольт-амперную характеристику (ВАХ) в аналитической форме. Для двухполюсного нелинейного элемента ВАХ характеризует зависимость его тока от приложенного напряжения i(u); многополюсные НЭ описываются проходной характеристикой Рассмотрим аппроксимацию в виде степенного полинома на примере биполярного транзистора, включенного по схеме с общим эмиттером. Его проходная ВАХ описывается зависимостью
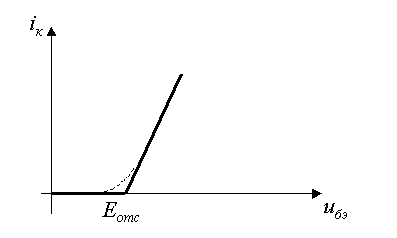
Рис.1. В общем случае аппроксимирующий полином имеет вид
где
Коэффициент Рассмотрим частные случаи. 1.Рабочая точка находится на линейном участке характеристики, а изменения входного напряжения таковы, что мгновенное значение тока не выходит за пределы линейного участка. В этом случае при аппроксимации можно ограничиться полиномом первой степени:
Часто коэффициент Данный вид аппроксимации используется при анализе усилителей слабого сигнала, а рабочая точка обычно выбирается на середине самого крутого линейного участка (точка 2.Рабочая точка расположена на нижнем нелинейном участке ВАХ (точка
где Если откуда
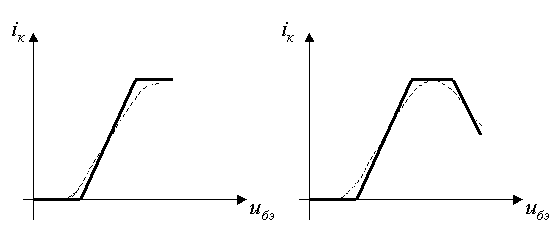
3.Рабочая точка является точкой перегиба характеристики, а изменения входного сигнала достаточно велики (см. рис.2).
Рис.2 . В точке перегиба все производные четного порядка равны нулю. Поэтому
Если
Напряжение
Аппроксимация в виде кубичного полинома допустима при Во всех иных случаях положения рабочей точки и изменениях входного напряжения полиноминальная аппроксимация требует более высокой степени. При этом анализ усложняется и применение степенного полинома для практических расчетов оказывается неэффективным. При очень больших изменениях сигнала более целесообразной оказывается кусочно-линейная аппроксимации. При этом для построения характеристики транзистора с ОЭ в режиме большого сигнала можно использовать следующие идеализации: а) статические входные ВАХ можно считать независимыми от
Рис.3.
б) статические выходные характеристики в активной области идут параллельно друг-другу; линия насыщения совпадает с осью ординат (см. рис.4).
Рис.4. При такой идеализации проходная характеристика
Рис.5 . Иногда приходится использовать более сложные идеализации, если мгновенные значения сигналов таковы, что реальные проходные ВАХ имеют участки насыщения или падающие участки. Эти случаи показаны на рис. 6 а, б.
а).б). Рис.6. Кусочно-ломаная (или кусочно-линейная) аппроксимация особенно проста и удобна для анализа преобразования сигналов в тех случаях, когда основное значение имеет нижний нелинейный участок (рис.5). При большом числе аппроксимирующих отрезков преимущества теряются. В этих случаях применяют различные трансцендентные функции, например гиперболический тангенс, экспоненты и др.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Наиболее широко распространены способы представления нелинейных ВАХ в виде полиномов или линейно-ломаных отрезков. Полиноминальная аппроксимация используется обычно при достаточно малых изменениях входного напряжения в окрестности рабочей точки, а линейно-ломаная - при больших.
. Наиболее широко распространены способы представления нелинейных ВАХ в виде полиномов или линейно-ломаных отрезков. Полиноминальная аппроксимация используется обычно при достаточно малых изменениях входного напряжения в окрестности рабочей точки, а линейно-ломаная - при больших. . Степень полинома, которой можно ограничить аппроксимирующую функцию, зависит от положения рабочей точки и величины входного напряжения. На рис.1 показан график функции
. Степень полинома, которой можно ограничить аппроксимирующую функцию, зависит от положения рабочей точки и величины входного напряжения. На рис.1 показан график функции 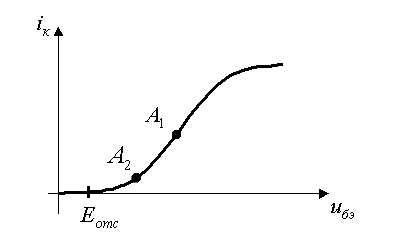
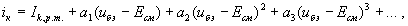
 - ток коллектора в рабочей точке при
- ток коллектора в рабочей точке при  - постоянное смещение перехода база-эмиттер(рабочая точка),
- постоянное смещение перехода база-эмиттер(рабочая точка),  - коэффициенты полинома, причем
- коэффициенты полинома, причем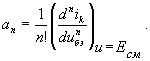
 представляет собой крутизну (производную) характеристики в рабочей точке,
представляет собой крутизну (производную) характеристики в рабочей точке,  - первую производную от крутизны (с коэффициентом 1/2) и т.д. Ясно, что коэффициенты
- первую производную от крутизны (с коэффициентом 1/2) и т.д. Ясно, что коэффициенты 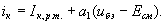
 называют крутизной и обозначают буквой S.
называют крутизной и обозначают буквой S. на рис.1).
на рис.1). на рис.1), имеющем вид квадратичной параболы. При этом предполагается, что мгновенное значение входного напряжения не заходит за точку
на рис.1), имеющем вид квадратичной параболы. При этом предполагается, что мгновенное значение входного напряжения не заходит за точку  , где
, где  - напряжение отсечки нелинейного элемента (начало характеристики). В этом случае аппроксимирующий полином можно ограничить второй степенью:
- напряжение отсечки нелинейного элемента (начало характеристики). В этом случае аппроксимирующий полином можно ограничить второй степенью: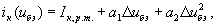
 .
. - крутизна ВАХ в рабочей точке, то величину
- крутизна ВАХ в рабочей точке, то величину  можно определить из условия:
можно определить из условия:  ,
,  . В этом случае
. В этом случае  ,
,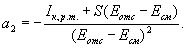
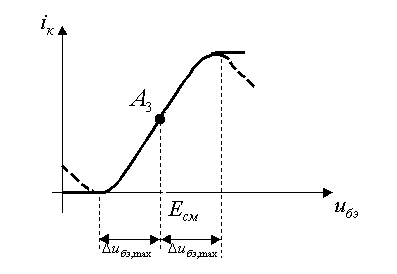

 , можно ограничиться полиномом третьей степени без квадратичного члена (пунктир на рис.24):
, можно ограничиться полиномом третьей степени без квадратичного члена (пунктир на рис.24):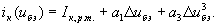
 иногда называют напряжением насыщения. Задавая это напряжение и зная величину
иногда называют напряжением насыщения. Задавая это напряжение и зная величину  , однозначно определяется величина
, однозначно определяется величина  :
: ,
, .
. ; нижний нелинейный участок спрямляется до пересечения с осью абсцисс; эта точка определяет напряжение
; нижний нелинейный участок спрямляется до пересечения с осью абсцисс; эта точка определяет напряжение  от
от  , т.е. выходные характеристики не зависят от того, при каком параметре они сняты (см. рис.3.);
, т.е. выходные характеристики не зависят от того, при каком параметре они сняты (см. рис.3.);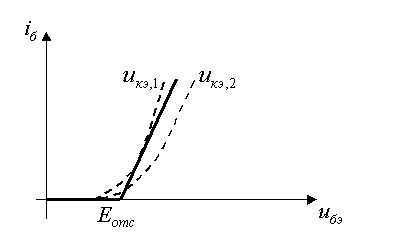
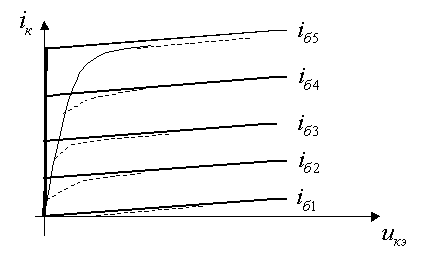
 будет иметь вид кусочно-линейной, показанной на рис.5.
будет иметь вид кусочно-линейной, показанной на рис.5.