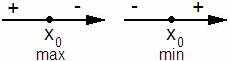|
|
Тема 2: Дифференциальные вычисления функции одной переменнойВопросы к экзамену по математике Программа минимум: Тема 1: Введение в математический анализ: 1) Определение функций одной вещественной переменной; ее области определений и области значений.
Функцией f называется правило, по которому каждому элементу одного множества D ставится в соответствии другое множество Е. Y=F(X), где X- независимая переменная Y- зависимая переменная
Область определения функции (D(y)) – множество значений, которые принимает Х Область значения (Е(y)) – множество значений, которое принимает y, когда Х «приобретает» область определения (D(y)).
2) Графики и свойства основных элементарных функций; определение элементарной функции. Элементарная функция – функции, построенные из основных и элементарных чисел, с помощью конечного числа арифметических действий и конечного числа взятия функций от функций.
· Степенная y=x^m, где m - вещественное число · Показательная y=a^x, где а – вещественное число (а>0 0<a<1) · Логарифмическая y=log a (x) (а>0 0<a<1) · Тригонометрические y=sin (x) y=cos(x) y=tg(x) y=ctg(x) · Обратные тригонометрические y=arcsin (x) y=arccos(x) y=arctg(x) y=arcctg(x)
3) БМ и ББ; что это такое. Функция называется БМ при ХàХ0 или Хà+-¥, если ее предел при этом стремление Х равен 0: Lim f(x)=0 Lim f(x)=0 x-->0 x-->+-¥
Функция называется ББ при X--> X0, если для любого положительного числа M найдется такое положительное b>0,, что для всех X, удовлетворяющих неравенству X<>X0 |X-X0|<b будет выполнено неравенство |f(x)|>M .
4) a и b: связь между ними.
· Если Lim · Если Lim · Если Lim · Если Lim
5) Правило Лопиталя. Если: 1. 2. 3. 4. существует то существует
6) Нахождение точек разрыва; исследование характера разрыва. План действий: · Находим D(y), это и есть разрыв · Находим предел слева и справа · Говорят, что функция f(x) имеет точку разрыва первого рода при x=a, если в это точке: существуют левосторонний предел limx→a−0f(x) и правосторонний предел limx→a+0f(x); эти односторонние пределы конечны.(т.е. пределы равны числу) · Функция f(x) имеет точку разрыва второго рода при x=a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. (т.е. пределы равны ¥)
Тема 2: Дифференциальные вычисления функции одной переменной
1) Формальное определение производной; смысл производной; механический и геометрический смысл производной. Производной функции y=f(x) по аргументу х в точке х0 называется предел отношения превращения функций с соответствующем приращению аргумента вычисленный при условии, что превращение аргумента произвольным образом стремиться к 0:
F ¢(x) = lim
Смысл производной - это скорость изменения функции у по отношению к аргументу х в точке х0. Механический смысл производной: производная пути по времени Геометрический смысл производной: производная
2) Правила и формула дифференцирования.
3) Уравнение касательной.
4) Дифференциал функции и приращение; связь этих величин. Дифференциал функции – это произведение производной функции на приращение ее аргумента. Dy=y ¢(x)* Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента, а разность f(x1)−f(x0)–приращением функции. 5) Дифференциал для приближенных значений. Пример 1: Y=8 Решение: Y’=8 Y’(x0)=y’(1)=-4
Пример 2: Y=
Y’= Y’(x0)=y’(2)=12
6) Теорема Лагранджа. Теорема Лагранжа о среднем значении утверждает, что если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), то в этом интервале существует хотя бы одна точка x=х0, такая, что
f(b)−f(a)=f′(х0)(b−a).
7) Определение возрастания и убывания функции; признаки возрастания и убывания дифференцируемой функции. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) > f(x1).
Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) < f(x1). Достаточный признак возрастания функции. Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I. Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I. 8) Определение локальных максимумов и минимумов функции; необходимые условия экстремума; первый достаточный признак экстремума
Говорят, что функция f(x) имеет локальный максимум в точке x0, если для всех точек x≠x0, выполняется неравенство f(x)<f(x0). Говорят, что функция f(x) имеет локальный минимум в точке x0, если для всех точек x≠x0, выполняется неравенство f(x)>f(x0). (Необходимое условие экстремума) Если функция Первый достаточный признак экстремума: Пусть f(x) непрерывна в некоторой окрестности точки х0 и имеет в этой окрестности производную всюду, кроме, быть может самой точки, тогда, если при x<x0 f ‘(x)>0 или при x>x0 f ‘(x)<0 - x0 точка макс. если при x<x0 f ‘(x)<0 или при x>x0 f ‘(x)>0 - х0 точка мин.
9) Определение асимптоты кривой; поиск наклонной и вертикальной асимптоты.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
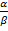 =0 è то a называется БМ более высокого порядка, чем b . a->0 несравнимо быстрее, чем b.
=0 è то a называется БМ более высокого порядка, чем b . a->0 несравнимо быстрее, чем b. или
или 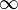 ;
;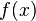 и
и  дифференцируемы в окрестности
дифференцируемы в окрестности 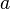 ;
; в окрестности
в окрестности  ,
, .
. = lim
= lim 

 есть скорость точки в момент
есть скорость точки в момент  :
:  .
. есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой
есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой  в точке
в точке  , т.е.
, т.е.  .
.
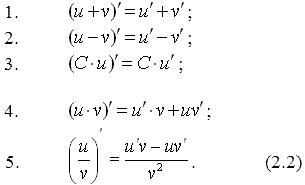

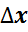
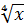 +
+  x от 1 до 0,98
x от 1 до 0,98 где х0=1
где х0=1 
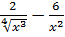
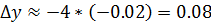
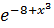 x
x 
 где х0=2
где х0=2 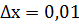
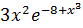

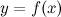 имеет экстремум в точке
имеет экстремум в точке  , то ее производная
, то ее производная  либо равна нулю.
либо равна нулю.