
|
|
Метод простой итерации ( метод Якоби)Метод деления пополам Пусть на отрезке Вычисляется точка
Пусть на к-м шаге найден отрезок Алгоритм завершается, если для некоторого к окажется Метод хорд Пусть
Вычтем из первого уравнения второе:
Уравнение принимает вид:
Таким образом, теперь можем найти первое приближение к корню, полученное методом секущих:
Теперь возьмем координаты
Повторять операцию следует до тех пор, пока Метод касательных Пусть на отрезке а
Метод касательных имеет (когда сходится) квадратичную скорость сходимости Модифицированный метод касательных Если мы хотим избежать вычисления производной на каждом шаге, то можно взять
В отличие от обычного метода касательных, в модифицированном методе предоставляется меньше требований к выбору начального приближения, а так же гарантировано отсутствие деления на ноль, если Метод простых итерации. Для построения рабочей формулы уравнение
Далее итерационный процесс строится по формуле
Для сходимости итерационного процесса (2) необходимо задать произвольное начальное приближение
Процесс (3) заканчивается при одновременном выполнении двух условий: К виду x=j(x), удобному для итераций, уравнение f(x)=0 можно привести разными способами. Один из способов заключается в следующем. Уравнение x=x+сf(x) Здесь функция Комбинированный метод Суть комбинированного метода состоит в разбиении отрезка [a,b] (при условии f(a)f(b)<0) на три отрезка с помощью хорды и касательной и выборе нового отрезка от точки пересечения хорды с осью абсцисс до точки пересечения касательной с осью абсцисс, на котором функция меняет знак и содержит решение. Условие начальной точки для метода хорд f(x)f”(x)<0. Входные данные: f(x), f’(x), f”(x), a, b, ε.
Метод Гаусса Дана система уравнений Для удобства вычислений используют расширенную матрицу (
Прямой ход.На каждом из шагов с номерами k = 1, …, n-1 выбираем ведущую строку с номером k и ведущий элемент 1). Все элементы ведущей строки расширенной матрицы делим на
2). Из всех строк расширенной матрицы с номерами i > k вычитаем ведущую строку, умноженную на элемент
3). Увеличиваем номер ведущей строки: k = k +1 и, если k < n, повторяем 1), 2). Если k = n, то прямой ход закончен. Обратный ход. По формулам
находим решение системы Метод Жордана-Гаусса Этот метод, как и метод Гаусса, является методом исключения, предназначенным для системы линейных уравнений
2). Из строк с номерами
Если элементы главной диагонали матрицы Метод Якоби Метод простой итерации ( метод Якоби) Пусть система линейных алгебраических уравнений (СЛАУ) задана в виде
Предположим, что диагональные элементы исходной системы не равны нулю (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему:
В системе (6) Теперь, задав нулевое приближение
Формулы (2.3) можно записать в виде
Условие окончания итерационного процесса
Достаточное условие сходимости. Если выполнено условие диагонального преобладания, то есть
то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием. См.15 Метод Зейделя Дана система линейных уравнений где Представив A в виде суммы двух матриц Уравнение (1a) преобразуем в реккурентную формулу метода Зейделя: Вычитая из обеих частей (2) Обозначив Из (2) можно получить расчетные формулы для
Таким образом, метод Зейделя отличается от метода Якоби тем, что, найдя
В качестве 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 локализован корень уравнения
локализован корень уравнения 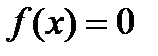 .
.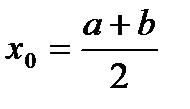 , если
, если 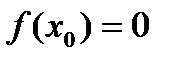 , то
, то 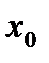 - корень уравнения. Если нет, то из двух половин
- корень уравнения. Если нет, то из двух половин  ,
, 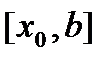 выбирают ту, на концах которой функция имеет противоположные знаки и полагают
выбирают ту, на концах которой функция имеет противоположные знаки и полагают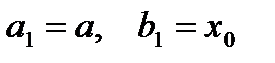 если
если  или
или 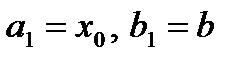 если
если  .
. . Тогда на к+1 шаге
. Тогда на к+1 шаге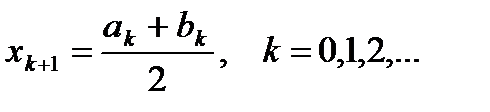
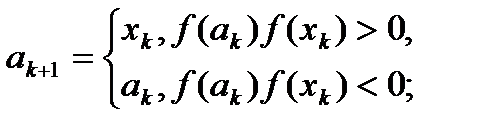
 .
. , где
, где  требуемая точность решения. Тогда значение корня
требуемая точность решения. Тогда значение корня  Если задана абсолютная точность определения корня
Если задана абсолютная точность определения корня  , то алгоритм завершается при условии
, то алгоритм завершается при условии  . В этом случае за приближенное значение корня
. В этом случае за приближенное значение корня  принимается
принимается 
 — абсциссы концов хорды, Найдем коэффициенты
— абсциссы концов хорды, Найдем коэффициенты  и
и  из системы уравнений:
из системы уравнений: .
. , затем найдем коэффициенты
, затем найдем коэффициенты  , тогда
, тогда .
.
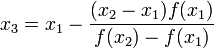
 и
и  и повторим все проделанные операции, найдя новое приближение к корню. Таким образом, итерационная формула метода секущих имеет вид:
и повторим все проделанные операции, найдя новое приближение к корню. Таким образом, итерационная формула метода секущих имеет вид: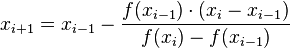 .
. не станет меньше или равно заданному значению погрешности.
не станет меньше или равно заданному значению погрешности. существует единственный корень уравнения (1):
существует единственный корень уравнения (1): 
 ,
, существует, непрерывна и отлична от нуля на
существует, непрерывна и отлична от нуля на 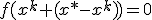 и применим к этому выражению формулу Лагранжа:
и применим к этому выражению формулу Лагранжа: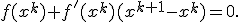 Выразим отсюда
Выразим отсюда  :
:

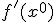 вместо
вместо  где
где  - начальное приближение:
- начальное приближение:
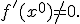
 преобразуется к виду:
преобразуется к виду: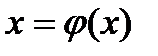 . (1)
. (1) (2)
(2) из отрезка
из отрезка  , для которого выполняется условие:
, для которого выполняется условие: (3)
(3)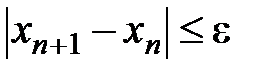 и
и  . В этом случае значение
. В этом случае значение  является приближенным значением корня нелинейного уравнения на отрезке
является приближенным значением корня нелинейного уравнения на отрезке  .
. . Тогда
. Тогда  Константа
Константа  выбирается из условия сходимости (3). Если производная
выбирается из условия сходимости (3). Если производная 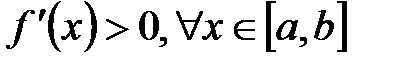 , то значение
, то значение 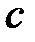 выбирается из интервала
выбирается из интервала 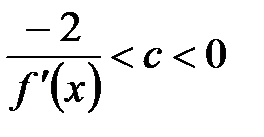 , если производная
, если производная  , то – из интервала
, то – из интервала 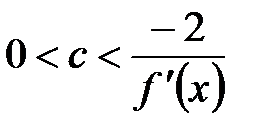 .
. 
 (1). Будем считать, что матрица системы А – неособенная. Требуется найти решение системы – вектор Х*.
(1). Будем считать, что матрица системы А – неособенная. Требуется найти решение системы – вектор Х*. 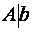 ), (n+1)-й столбец которой – столбец свободных членов системы - b:
), (n+1)-й столбец которой – столбец свободных членов системы - b:
 .
. . Далее выполняем следующие операции.
. Далее выполняем следующие операции. . (2)
. (2)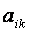 , получая нули под ведущим элементом:
, получая нули под ведущим элементом: . (3)
. (3)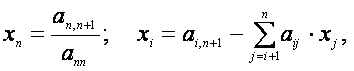
 (4)
(4) T .
T .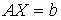 ( матрица А – невырожденная). Отличие от схем метода Гаусса в том, что путем преобразований матрица А приводится не к треугольному, а к диагональному виду. В результате исходная система линейных уравнений приобретает вид:
( матрица А – невырожденная). Отличие от схем метода Гаусса в том, что путем преобразований матрица А приводится не к треугольному, а к диагональному виду. В результате исходная система линейных уравнений приобретает вид:
 . Классическая схема Жордана реализуется за n шагов. Описание k-го шага (k =1,2...n).
. Классическая схема Жордана реализуется за n шагов. Описание k-го шага (k =1,2...n). :
: j = 1, 2, ...,n + 1.
j = 1, 2, ...,n + 1. вычитаем k-ю строку, умноженную на числовой коэффициент
вычитаем k-ю строку, умноженную на числовой коэффициент  так, чтобы в k-ом столбце расширенной матрицы получить нули над и под элементом
так, чтобы в k-ом столбце расширенной матрицы получить нули над и под элементом  :
: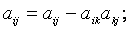 ж j = 1, 2, ...,n + 1.
ж j = 1, 2, ...,n + 1. в процессе работы метода оказываются равными или близкими к нулю, то можно использовать модификации метода с перестановкой строк или столбцов, аналогичные соответствующим модификациям метода Гаусса
в процессе работы метода оказываются равными или близкими к нулю, то можно использовать модификации метода с перестановкой строк или столбцов, аналогичные соответствующим модификациям метода Гаусса
 (6)
(6) -ое уравнение представляет собой
-ое уравнение представляет собой  -ое уравнение системы (6), разрешённое относительно
-ое уравнение системы (6), разрешённое относительно  –ой неизвестной (
–ой неизвестной (  ).
). , по соотношениям (5) можем выполнять итерационный процесс. Таким образом, рабочие формулы метода простой итерации решения системы (5) будут иметь вид
, по соотношениям (5) можем выполнять итерационный процесс. Таким образом, рабочие формулы метода простой итерации решения системы (5) будут иметь вид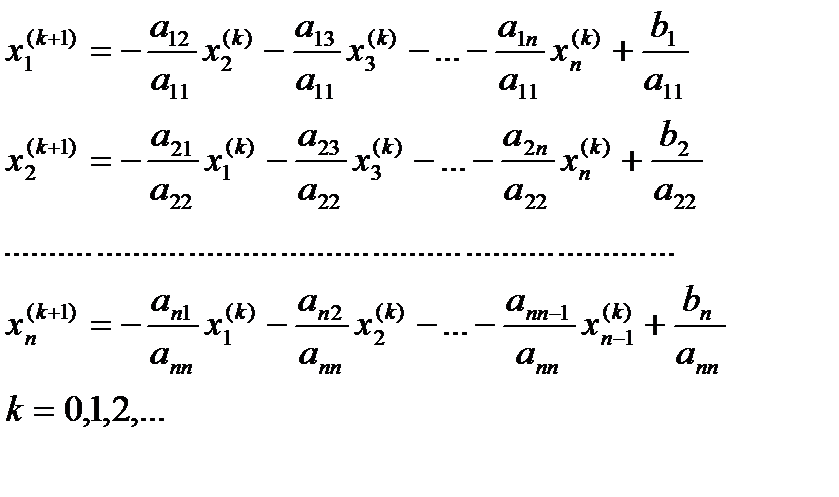
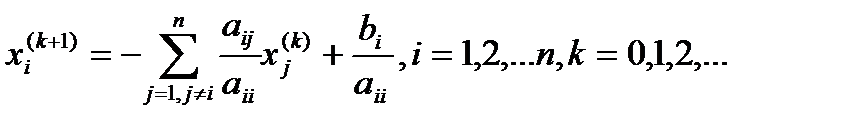
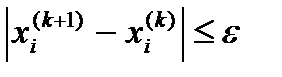 ,
,  .
.
 ,(1)
,(1)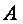 -квадратная невырожденная матрица.
-квадратная невырожденная матрица. , где
, где 
 ;
; 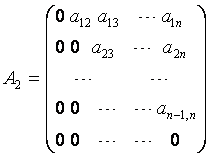 , запишем (1) в виде:
, запишем (1) в виде: (1a)
(1a)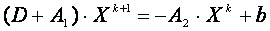 , k = 0,1,2,… (2)
, k = 0,1,2,… (2) , получим представление (2) в виде:
, получим представление (2) в виде: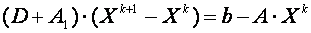 , k = 0,1,2,… (2a)
, k = 0,1,2,… (2a) ,
,  , получим расчетные формулы метода Зейделя в матричном виде:
, получим расчетные формулы метода Зейделя в матричном виде: ;
;  ,
,  0, 1, ... (3).
0, 1, ... (3). в координатной форме:
в координатной форме: ,
, 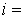 1, ..., n,
1, ..., n,  0, 1, ... . (4)
0, 1, ... . (4) , его сразу используют для вычисления
, его сразу используют для вычисления  (по начальным
(по начальным  ,
,  , ...,
, ..., 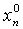 находят
находят  , затем, используя
, затем, используя  ,
,  , ...,
, ..., 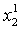 и т.д.).
и т.д.). можно взять любой, например, нулевой вектор. Критерий остановки расчетов:
можно взять любой, например, нулевой вектор. Критерий остановки расчетов: 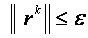 . Условием сходимости метода Зейделя является
. Условием сходимости метода Зейделя является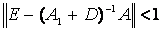 (5).
(5).