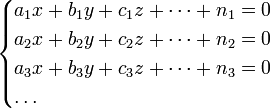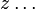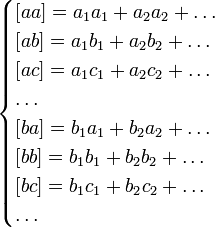|
|
Ход работы и обработка результатов измеренийТеория метода Рассмотрим систему связанных тележки и грузов. Расставим силы, действующие на тележку и грузы, и применим законы Ньютона.
 
 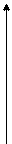    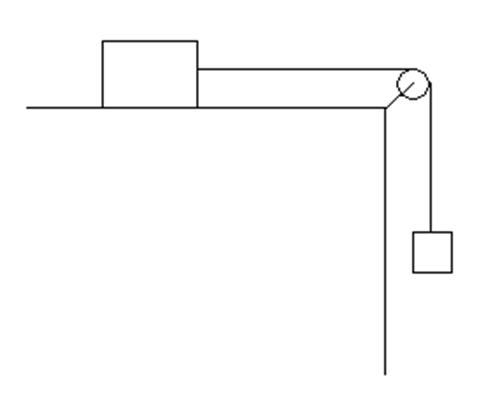
Рисунок 1 – Система связанных тележки и грузов По второму закону Ньютона
Т.к. блок и нерастяжимая нить невесомы, то
Учитывая (8,9) запишем (6,7) п проекциях на оси Ох и Оу:
Решая совместно (10) и (11), найдем ускорение тележки
Если тележка начала движение без начальной скорости, то зависимость скорости тележки от времени может быть записана как
а пути - как
Описание установки




 
Рисунок 1 – Экспериментальная установка Установка (Рисунок 1) состоит из алюминиевого рельса 3 длиной 1,5м, установленного горизонтально на лабораторном столе. На рельсе установлена тележка 2 с сапфировым основанием, обеспечивающим малое трение с поверхностью рельса. Масса тележки 0,4кг. Пусковое устройство 1 установлено таким образом, что тележка начинает движение без начальной скорости. Тележка связана легкой нерастяжимой нитью с держателем грузов, перекинутой через неподвижный легкий блок. Для измерения скорости на тележку сбоку крепится лёгкий тёмный экран длиной 0,1м. При движении тележки экран перекрывает свет в световом барьере 4, время перекрытия фиксируется таймером 5. Ход работы и обработка результатов измерений 1. Соберите установку как показано на рисунке 1. 2. Расположите дорожку горизонтально с помощью трех регулировочных винтов у ее основания. 3. Установите стартовую систему таким образом, чтобы спусковое устройство 1 спускало планер, не сообщая ему начальный импульс. 4. Подсоедините систему к двум выходам «Start» («Пуск») на таймере 5; следует соблюдать полярность при подсоединении. Красный выход системы подключается к желтому гнезду таймера. 5. Расположите четыре световых барьера 4 таким образом, чтобы они разделяли измеряемое расстояние на отрезки примерно равной длины. Последний барьер расположите так, чтобы тележка 2 с экраном проходила мимо него перед тем, как ускоряющая гиря коснется пола. 6. Четыре световых барьера подсоедините слева направо к контрольным гнездам «1»-«4» таймера. Соедините гнезда в соответствии с цветом. 7. Закрепите на тележке темный легкий экран. 8. По заданию преподавателя установите на тележку и/или держателе дополнительные грузы. 9. С помощью кнопки «MODE» выберите режим 10. В выбранном режиме измерьте четыре времени 11. Результаты измерений занесите в таблицу.
12. С помощью кнопки «MODE» выберите режим 13. В выбранном режиме измерьте четыре времени 14. Результаты измерений занесите в таблицы. Время ti рассчитайте по формуле:
15. Постройте графики зависимости пройденного пути от квадрата времени 16. Рассчитайте ускорение тележки методом наименьших квадратов
17. Рассчитайте скорости тележки в различные моменты времени.
18. Постройте графики зависимости скорости от времени 19. .Изменяя массу дополнительных грузов на тележке при фиксированной массе грузов на держателе ( 20. Постройте графики зависимости ускорения от обратной инертной массы 21. Изменяя массу дополнительных грузов на держателе и тележке при фиксированной массе системы ( 22. Постройте графики зависимости ускорения от силы
Контрольные вопросы 1. Дайте определение импульса материальной точки. 2. Как найти импульс тела? 3. Дайте определение массы и назовите ее свойства. 4. Дайте определение силы и назовите ее свойства. 5. Сформулируйте законы Ньютона. 6. Является ли первый закон Ньютона следствием второго? 7. Укажите границы применимости законов Ньютона. 8. Выведите рабочие формулы.
Заключение План оформления лабораторной работы: 1. Номер лабораторной работы. 2. Название лабораторной работы. 3. Цель работы. 4. Оборудование. 5. Краткая теория. 6. Описание установки. 7. Ход работы и обработка результатов измерений. Все расчеты, необходимые для получения окончательных результатов лабораторной работы, должны быть представлены в конспекте в форме, доступной для проверки преподавателем. Все расчеты должны проводиться в международной системе единиц измерения СИ. На основе проведенных расчетов в конспекте лабораторной работы (если это требуется) должны быть построены экспериментальные графики зависимостей физических величин, предусмотренные методическими указаниями. Требования по оформлению графиков: 1) Графики строятся на миллиметровой бумаге; 2) на графике: оси декартовой системы, на концах осей — стрелки, индексы величин, единицы измерения, множители; 3) на каждой оси указывается масштаб; 4) под графиком указывается его полное название; 5) на графике должны быть отмечены экспериментальные точки. Результаты расчета физических величин, которые должны быть получены как итог выполнения лабораторной работы. Окончательный результат должен быть представлен в виде среднего значения измеренной физической величины с указанием ее доверительного интервала. Вывод по лабораторной работе должен включать в себя сравнение полученных результатов с теоретическими положениями.
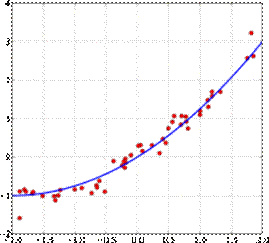
Приложение А Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки. Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке измерений. Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут среднее арифметическое из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов отклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов. Пример 1
Рисунок 8 - Кривая, проведённая через точки, имеющие нормально распределённое отклонение от истинного значения
Пусть надо решить систему уравнений
число которых более числа неизвестных x, y, Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной x и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной y и, сложив почленно, получают второе нормальное уравнение и т. д. Если обозначить для краткости:
то нормальные уравнения представятся в следующем простом виде:
Легко заметить, что коэффициенты нормальных уравнений весьма легко составляются из коэффициентов данных, и притом коэффициент у первой неизвестной во втором уравнении равен коэффициенту у второй неизвестной в первом, коэффициент у первой неизвестной в третьем уравнении равен коэффициенту у третьей неизвестной в первом и т. д. Для пояснения сказанного ниже приведено решение пяти уравнений с двумя неизвестными:
Составив значения [aa], [ab], получаем следующие нормальные уравнения:
откуда x = 3,55; y = − 0,109 При составлении обычной регрессионной модели используется та же методика, и данные коэффициенты представляют собой коэффициенты уравнения регрессии. Уравнения (1) представляют систему линейных уравнений, то есть уравнений, в которых все неизвестные входят в первой степени. В большинстве случаев уравнения, связывающие наблюдаемые и искомые величины, бывают высших степеней и даже трансцендентные, но это не изменяет сущности дела: предварительными изысканиями всегда можно найти величины искомых с таким приближением, что затем, разложив соответствующие функции в ряды и пренебрегая высшими степенями искомых поправок, можно привести любое уравнение к линейному.
Рекомендуемая литература 1. И.Е. Иродов. Механика. Основные законы. М.-С-Пб.: БИНОМ- Лаборатория знаний, 2009. 2. Курс физики. Учебник для вузов/под. ред. проф. В.Н. Лозовского. СПб: Лань, 2009. Т.1 3. И.В. Савельев. Курс общей физики. Том 1. Механика. C-Пб.-М.-Краснодар: ЛАНЬ, 2008. 4. Т.И. Трофимова. Краткий курс физики. Учебное пособие для вузов. М: КноРус, 2010. 5. Энциклопедический словарь Брокгауза и Ефрона (1890—1907).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
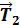
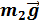
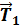
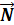

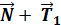 +
+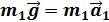 , (6)
, (6)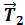 +
+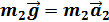 . (7)
. (7) , (8)
, (8)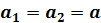 . (9)
. (9)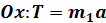 (10)
(10) (11)
(11)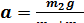 . (12)
. (12)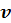 =
=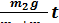 , (13)
, (13) . (14)
. (14) .
. . Повторите измерения три раза.
. Повторите измерения три раза.

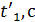
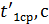
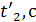
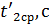

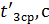
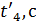
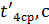
 .
.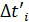 затемнения каждого барьера. Повторите измерения три раза.
затемнения каждого барьера. Повторите измерения три раза.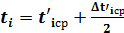 .
.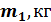

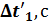
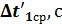
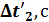

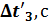
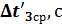
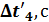
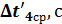
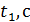

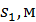
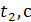
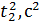

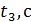
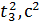

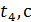
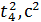
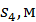
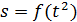 . Объясните их вид.
. Объясните их вид.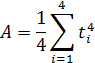
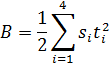
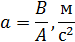
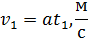

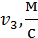
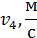
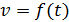 . Объясните их вид.
. Объясните их вид.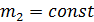 ) повторите п. 9-16.
) повторите п. 9-16.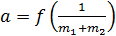 . Объясните их вид.
. Объясните их вид.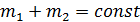 ) повторите п. 9-16.
) повторите п. 9-16.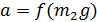 . Объясните их вид.
. Объясните их вид.