
|
|
Принцип наименьшего действия.12 Для каждой физической системы мы можем ввести функцию Лагранжа, описывающую эволюцию системы:
Ставится задача: как выбрать истинную траекторию. Введем понятие принципа наименьшего действия (ПНД):
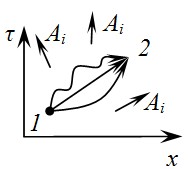
Истинная траектория между точками 1 и 2 - это та траектория, действие вдоль которой минимально. При переходе к четырехмерному пространству формулировка ПНД не меняется. Траектория – мировая линия. Рассмотрим пустое пространство и свободную частицу. Лагранжиан такой частицы:
Сформулируем дополнительное условие на ПНД исходя из равноправности систем отсчета: действие должно быть скалярным. Траектория также не должна изменяться из одной ИСО в другую ИСО.
Найдем выражение Лагранжиана для свободной частицы в четырехмерном пространстве и времени.
Разобьем траекторию на маленькие интервалы dS. inv
При V
Можно потребовать, что на малых скоростях Лагранжиан должен преобразовываться к классическому виду. Множитель αc = const – соответственно
Соответственно, зная функцию Лагранжа, можно установить характеристики частиц при любых скоростях.
E = При скорости движения равной нулю, любая частица обладает энергией (энергия покоя).
Если скорость частицы отлична от нуля, то полная энергия Из выражения для импульса и энергии частицы можно выразить связь между p и E.
Это выражение позволяет вычислить импульс частицы без массы, то есть если объект обладает энергией, то он обладает и импульсом. Приведем рассмотренные величины к четырехмерной форме записи.
Четвертой компонентой импульса является энергия, поэтому В четырехмерном мире нельзя рассматривать отдельно импульс и энергию, так как они являются компонентами одного вектора:
Алгоритм отыскания преобразования величины при переходе из одной ИСО в другую: 1. Определение трехмерной величины как четырехмерной 2. Применение преобразования 3. Раскрытие индексной формы записи
Найдем четырехмерную функцию Гамильтона:
_______________________________________ X мерный потенциал Перейдем к описанию электрических явлений. ЭМП р/м как самостоятельно существующий объект. Для выявления существования поля проведем мысленный эксперимент.
Частицы движутся равномерно. Относительно движущейся системы события в точке А и В будут неодновременными. С точки зрения движущегося наблюдателя события в точке А наступит раньше, чем в В |=> в какой-то момент времени первая частица будет двигаться без ускорения, а вторая ускоренно |=> изменится импульс системы на некотором промежутке времени |=> нарушается закон сохранения импульса (этого быть не должно) |=> в нашей системе чего-то нахватает. Способ разрешения парадокса - предположение существования 3-го объекта – ЭМП. Данный прим. показывает, что ЭМП существует как самостоятельный объект. Заряженные частицы никогда не взаимодействуют друг с другом. Они всегда взаимодействуют с полем.
Каковы обобщенные координаты ЭМП? Обобщение большого количества материальных факторов приводит к утверждению, что заряд частицы полностью описывает эл.маг. свойства этой частицы. Заряд - это скаляр инвариант. ЭМП полностью и однозначно описывается 4-х вектором Ai(ri). Этот вектор мы будем называть 4-х мерным потенциалом ЭМП. Ai – принадлежит всему пространству. Обратимся к принципу наименьшего действия. Действие для частицы, находящейся в ЭМП, можно описать как
При наличии поля лучшей траекторией будет не прямая, а кривая. Это обусловлено существованием потенциала Исходя из этих позиций найдем функцию Лагранжа для частицы во внешнем ЭМП.
Обобщим полученный результат:
Интервал и причинность Интервалом называется характеристика для двух любых событий, которая определяется так:
Интервал является кривой, не зависящей от системы отсчёта, то есть интервал инвариантная величина. Рассмотрим частные случаи 1) 2)
3)
Установим причинно – следственную связь между событиями. Если информация приходит в некоторую точку, то эта точка является следствием, какого-то события. Пусть мы рассматриваем точку 1, и все события рассматриваем относительно неё. Данная фигура - трёхмерный конус в четырёхмерном пространстве. Нижняя часть конуса является областью абсолютного прошлого конуса. Верхняя его часть называется областью абсолютного будущего. Область вне конуса называется абсолютно удалённой. Событие 1 – следствие любого из событий снизу и причина любого из событий сверху. Для любого события внутри конуса интервал является времениподобным, вне конуса по отношению к 1 – пространственноподобным. _______________________________________ 10. Калибровочная инвариантность. Функция Гамильтона. Для того, чтобы найти вектор электрического поля, мы должны, исходя из уравнения движения, поместить частицу в поле и измерить силу
Второй шаг – измеряем силу, действующую на неподвижную частицу, вычитаем кулоновскую силу, => определяем вектор Это главный и единственный способ определения Если Да, можно восстановить, но неоднозначно.
Мы убедились, что потенциалы определены неоднозначно. Преобразование потенциалов, не изменяющее векторов поля называется калибровочным преобразованием или градиентным преобразованием.
Принцип калибровочной инвариантности: Всякое математическое выражение, описывающее измеряемые характеристики электромагнитного поля, не должно меняться при калибровочных преобразованиях потенциалов.
Тензор ЭМП. Если мы покоимся в системе, то на нее не действуют силы. Если же мы находимся в движущейся системе, то
Необходимо найти инвариантное написание четырехмерной формы для электромагнитного поля.
Вернемся к рассмотрению заряженной частицы во внешнем элементарном поле. Повторим вывод в четырехмерной форме.
Если выбранная траектория истина, то действие по очень близкой траектории будет больше.
Вариация действия вдоль истиной траектории равна нулю. Раз это справедливо, воспользуемся этим.
Домножим на
Продифиринцируем это выражение:
Под знаком интеграла останется:
Так как
Подставим данные записи в исходный интеграл, получим:
произведем замену:
(четырехмерное обобщение уравнения движения частицы в поле)
(характеристическое силовое воздействие поля, тензор эл.маг. поля)
Эл.маг. поле опр-ся так же как и тензор
_______________________________________ 13. Инварианты электромагнитного поля. Есть ли у магнитного поля величины, которые являются инвариантами
в этом произведении каждый элемент умножается сам на себя
При переходе из одной системы в другую : Введем понятие единичного антисимметричного тензора
0,если два индекса из iklm совпадают; 1,соотвествует четным перестановкам этих индексов и если все индексы отличаются друг от друга; -1,если все индексы отличны и составляют нечетную перестановку
Пример
Нечетной перестановкой называют такую перестановку, в которой мы производим замену нечетное количество раз.
Четной перестановкой называют такую перестановку, в которой мы производим замену четное количество раз.
-8i( Вид угла (острый, тупой, прямой) между векторами Т.е., меняя систему отсчета, мы можем добиться любых значений векторов Других базовых инвариантов у электромагнитного поля – нет.
+ 1 2 3 4 - 1 2 4 3 - 1 3 2 4 + 1 3 4 2 + 1 4 2 3 - 1 4 3 2 - 2 1 3 4 + 2 1 4 3 + 2 3 1 4 - 2 3 4 1 - 2 4 1 3 + 2 4 3 1 + 3 1 2 4 - 3 1 4 2 - 3 2 1 4 + 3 2 4 1 + 3 4 1 2 - 3 4 2 1 - 4 1 2 3 + 4 1 3 2 + 4 2 1 3 - 4 2 3 1 - 4 3 1 2 + 4 3 2 1

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

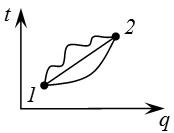
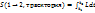 – действие вдоль траектории.
– действие вдоль траектории. , траектория – прямая линия.
, траектория – прямая линия.
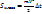




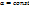 – не меняет сущности действия
– не меняет сущности действия



 ,
,  =>
=>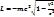 – релятивистское выражение для Лагранжиана свободной частицы.
– релятивистское выражение для Лагранжиана свободной частицы. ,
,  ,
, =
=  ,
,  =
=  =
=  ,
,  =
=  =
=  ,
,  =
=  =
= 
 =
= 

 +
+  +
+  - L =
- L =  + m
+ m 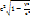 = E =
= E =  =
= 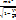
 =
=  - формула Эйнштейна, это есть следствие инвариантности ПНД.
- формула Эйнштейна, это есть следствие инвариантности ПНД. .
.
 = (
= ( 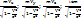 )
)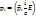
 энергии.
энергии. =
= 
 ),
),  ,
,  ,
,  = γ(i
= γ(i  +
+  )
) - i
- i 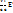 ) = γ(
) = γ(  )
) = γ(
= γ(  +
+  ) => E=γ(V
) => E=γ(V  =
=  =
=  = -m
= -m  =
=  +
+  +
+  +
+ 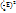 =
=  -
- 
 =
= 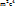 +
+ 



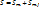 . Где
. Где  - действие свободной частицы,
- действие свободной частицы,  – взаимодействие частицы и поля
– взаимодействие частицы и поля
 предполагается что
предполагается что  - заданная величина.
- заданная величина.


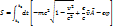



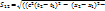


 > 0. Это возможно, когда пространственные координаты не вносят существенного вклада в величину интервала. Такой интервал называется времени подобным.
> 0. Это возможно, когда пространственные координаты не вносят существенного вклада в величину интервала. Такой интервал называется времени подобным. 

 пространственные и временные координаты вносят одинаковый вклад. Такие интервалы называются нулевыми или световыми.
пространственные и временные координаты вносят одинаковый вклад. Такие интервалы называются нулевыми или световыми.

 .
. и
и  и
и  . Через эти опр-ния не видно прямого способа измерения
. Через эти опр-ния не видно прямого способа измерения 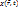



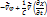

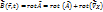





 - энергия частицы во внешнем поле. Она состоит из энергии свободной частицы и энергии воздействия поля.
- энергия частицы во внешнем поле. Она состоит из энергии свободной частицы и энергии воздействия поля.
 Получим четырехмерный объект, описывающий четырехмерное поле.
Получим четырехмерный объект, описывающий четырехмерное поле.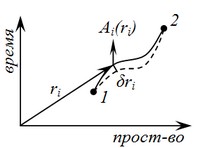
 - вариация траектории.
- вариация траектории.


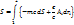


 :
: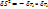
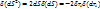


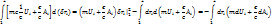


 - функция, которая зависит от координат радиус-вектора.
- функция, которая зависит от координат радиус-вектора.


 :
: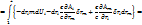









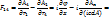


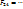










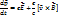



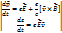
 ;
;  - 4тензор 4-го ранга
- 4тензор 4-го ранга
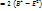 - скаляр inv (инварианта)
- скаляр inv (инварианта) 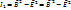
 исходя из инварианта
исходя из инварианта  , если для некоторого наблюдателя
, если для некоторого наблюдателя 



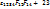 слагаемых = 8
слагаемых = 8  (-i
(-i  )-8(-
)-8(-  )(-i
)(-i  )+8
)+8 
 )= -8i (
)= -8i (  )=inv=
)=inv= 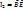
 остаются такими же во всех системах отсчета.
остаются такими же во всех системах отсчета.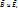 однако инварианты
однако инварианты 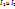 сохраняют свои значения.
сохраняют свои значения.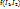 – inv ЭМП (инвариант электромагнитного поля)
– inv ЭМП (инвариант электромагнитного поля)