
|
|
ТЕПЛОВЫЕ РАСЧЕТЫ В ЭЛЕКТРИЧЕСКИХ МАШИНАХ И ТРАНСФОРМАТОРАХ
Задание № 1 Задачей тепловых расчетов является определение температуры активных частей машины и трансформаторов с целью поверки выполнения требований по допустимому уровню нагрева. В первую очередь это касается изолированных обмоток. Тепловой расчет. Как правило выполняется для номинального режима при установившемся состоянии нагрева. В большинстве случаев достаточно ограничится расчетом средних превышений температуры, в частности, для обмоток, поскольку они легко измеряются методом сопротивления при испытаниях, а их допустимые значения определены в стандартах для различных классов нагревостойкости изоляции. Ниже приводятся задания по тепловым расчетам электрических машин и трансформаторам для студентов бакалавриата и специалитета всех форм обучения. Изоляция паза электрической машины состоит из нескольких слоев разнородных электроизоляционных материалов (рис. 2.1). Рис. 2.1.
Предположим, что пазы заполнены недостаточно плотно и между слоями изоляции, а также между проводниками обмотки и изоляцией и стенками паза имеются воздушные прослойки толщиной δв = 0,1 мм. Требуется: 1.Определить эквивалентный коэффициент теплопроводности пазовой изоляции при наличии воздушных прослоек. 2.Определить эквивалентный коэффициент теплопроводности пазовой изоляции для случая, когда воздушные прослойки полностью заполнены пропиточным лаком, коэффициент теплопроводности которого λ1=0,25 Вт/(м·град).
Таблица 2.1 Исходные данные к задаче №1
3.Дать оценку влияния пропитки на эквивалентный коэффициент
Методические указания Анализ конструкции пазовой изоляции электрической машины показывает, что толщина изоляции, по сравнению с периметром паза и его длиной, очень мала. Поэтому задача сводится к решению одномерного температурного поля, причем передача тепла происходит поперек слоев изоляции. Результирующее удельное термическое сопротивление определяется по формуле Rрез= где δ1 - толщина i- го слоя, м; λi - коэффициент теплопроводности i-го слоя, Вт/(м·град); n - количество слоев изоляции, включая и воздушные прослойки. С другой стороны, данную изоляцию можно представить однородной изоляцией той же ширины Rрез= Тогда эквивалентная теплопроводность пазовой изоляции определяется следующим образом:
Теплофизические свойства воздуха при рабочей температуре обмотки можно определить по таблице 1.2. Разница между п.1 и п.2 данной задачи состоит в том, что в первом случае обмотка является непропитанной, а во втором - пропитана лаком с известными теплофизическими свойствами.
Задание №2.
В баке трансформатора, имеющем толщину стенки δσ и высоту 1 м, находится трансформаторное масло. Наружная поверхность бака охлаждается воздухом. Известны: средний тепловой поток с единицы поверхности - qδ, коэффициенты теплоотдачи бака со стороны масла - α1, со стороны воздуха - α2, коэффициент теплопроводности бака - λδ.
Многослойная цилиндрическая обмотка трансформатора, выполненная проводом прямоугольного сечения, имеющая эквивалентный коэффициент теплопроводности λэкв, с двух сторон омывается трансформаторным маслом. Толщина обмотки 2δ мала по сравнения с высотой и диаметром цилиндра обмотки. Коэффициент теплоотдачи на поверхности обмотки α0= α2; объемная плотность внутреннего тепловыделения обмотки qv. Данные, необходимые для решения своего варианта задачи, приведены в таблицах 2.2а и 2.2б.
Таблица 2.2а Исходные данные к заданию №2
Требуется: 1. Определить термическое сопротивление между трансформаторным маслом и стенкой бака, термическое сопротивление бака, термическое сопротивление между стенкой бака и окружающим воздухом и общее термическое сопротивление теплопередачи Rтп. 2. Определить общий перепад температуры между трансформаторным маслом и воздухом θЖ1- θЖ2 и составляющие этого перепада: масло-бак, в баке и бак-воздух. Дать сравнительную оценку этих составляющих. 3. Определить температуру масла θЖ1. 4. Найти температуру на поверхности обмотки θПО. 5. Определить максимальную температуру обмотки 6. Рассчитать среднюю температуру обмотки θОср. Сравнить ее с допустимой температурой для изоляции класса А.
Таблица 2.2б Исходные данные к заданию №2
7. Построить график изменения температуры в зависимости от координаты (рис. 2.2) 8. Определить срои службы изоляции обметки трансформатора при полученной из расчета средней температура обмотки. 9. Определить температуру трансформаторного масла и среднюю температуру обмотки, а также срок службы изоляции обмотки, если коэффициент теплоотдачи с поверхности бака со стороны воздуха увеличить в 2 раза за счет обдува вентилятором. Построить в тех же координатах (рис. 2.2) в масштабе по температуре второй график при увеличении коэффициент теплоотдачи с поверхности бака со стороны воздуха в 2 раза. Методические указания Поскольку толщина цилиндрической обмотки мала по сравнение с диаметром цилиндра, то кривизной обмотки можно пренебречь и рассматривать задачу как для плоской стенки. Толщина обмотки мала по сравнению с ее высотой, поэтому можно пренебречь изменением температуры по высоте обмотки. В этом случае задача сводится к решение одномерного температурного поля в плоской стенке при наличии источников внутреннего тепловыделения (см. учебник § 7.1 [1, с. 104-114]). Среднюю допустимую температуру для различных электроизоляционных материалов можно определить по ГОСТ 26772 – 85.. Необходимо сделать сравнение рассчитанного значения средней температуры с допустимой. В случае, если эти величины сильно отличаются друг от друга, то необходимо определить срок службы изоляции обмотки и дать рекомендации по изменению условий теплообмена между обмоткой и трансформаторным маслом. При выполнении задачи обратить внимание на правильное использование обозначения тепловых величин и их единиц измерения. При определении термических сопротивлений необходимо прежде всего узнать характер каждого из термических сопротивлений и оценить влияние каждого из них на температуру трансформаторного масла и обмотки. При решении задачи предполагается, что охлаждение обмотки с обеих сторон одинаковое. В этом случае плотности теплового потока на их поверхностях также будут одинаковыми и определяться потерями, выделяемыми в половине объёма по толщине обмотки. Тогда: qпо = qv ∙ δ. Обратите внимание, что объемная плотность внутреннего тепловыделения обмотки qv в таблице 2.2б задана в тысячах единиц. При определении плотности теплового потока с единицы поверхности бака принять ее равной удвоенному значению плотности теплового потока на поверхности обмотки: qб = 2∙qпо. Температура обмотки θЖ2 = θо.с = +40оС. Тогда наибольшее значение температуры обмотки
где ∆θПО-М - перепад температуры между поверхностью обмотки и маслом; ∆θМ-Б - перепад температуры между маслом и поверхностью бака; ∆θБ - перепад температуры внутри бака;
В установившемся режиме нагрева величина потерь в обмотке трансформатора является неизменной величиной, поэтому величина теплового потока, который выделяется в обмотке и проходит через её поверхности, масло и бак, остается постоянной. Поэтому перепады температуры определяются внутренними тепловыми сопротивлениями обмотки и бака и условиями теплоотдачи на поверхностях. Расчет теплового потока с некоторого участка i поверхности площадью S выполняют по формуле Ньютона – Рихмана Q = αi∙S∙( θСi- θЖi).
Рис. 2.2. Пример построения графика изменения температуры в трансформаторе (в масштабе по значениям температуры; дать их численные значения)
Тогда перепад температуры между поверхностью стенки и охлаждающей средой можно выразит через плотность теплового потока в форме закона Ома (см. учебник § 6.1 [1, с. 92-93]):
где 1/αi – удельное тепловое сопротивление теплоотдачи. Перепад температуры внутри стенки бака может быть определен на основе решения дифференциального уравнения теплопроводности и уравнения Фурье для плоской стенки без внутренних источников тепла (см. учебник § 7.1 и § 7.2 [1, с. 104-117]). Это решение, переписанное в форме закона Ома, имеет следующий вид:
где ∙dб / lб – удельное термическое сопротивление теплопроводности стенки бака, толщиной∙dб. Перепад и характер изменения температуры внутри обмотки может быть определен на основе решения дифференциального уравнения теплопроводности и граничных условий III рода для плоской стенки с внутренними источниками тепла (см. учебник § 7.1 [1, с. 104-114]). Это решение имеет следующий вид:
где ∆θПО-М = qпо / α1. Таким образом, в соответсвии с приведенным выше выражением график изменения температуры внутри обмотки трансформатора имеет вид параболы с вершиной в координате x = 0. Тогда максимальная температура обмотки в координате x = 0 (рис.2.2) будет равна θО = qv∙δ2/(2∙λэкв) + ∆θПО-М+ θЖ1. Первое слагаемое в этом выражении представляет собой перепад температуры внутри обмотки Для определения срока службы определяют среднее значение температуры обмотки θОср = qv∙(δ2 – x2)/(3 λэкв) + ∆θПО-М+ θЖ1. Срок службы обмоток трансформатора при изоляции класса А определяется по правилу Монтзингера:
где D105-срок службы при температуре 105о для изоляционных материалов класса А. Принимаем D105 = 10 лет; Δθ-постоянная величина приращения температуры, сокращающая срок службы вдвое. Для изоляционных материалов класса А принимают Δθ=8оС. Задание №З.
Двигатель постоянного тока характеризуется данными, приведенными в табл. 2.3. Требуется: 1.Составить эквивалентную тепловую схему (ЭТС) замещения якоря (рис. 2.3). 2. Вычислить термические, сопротивления, входящие в эквивалентную тепловую схему замещения (рис. 2.4), и произвести ее преобразование к простейшему виду (рис. 2.5). 3. Определить средние превышения температуры отдельных частей машины и сделать заключение о соответствии теплового состояния машин требованиям ГОСТ.
Рис. 2.3 Конструктивная схема якоря
Рис. 2.4 Исходная ЭТС якоря машины постоянного тока
Таблица 2.3
Продолжение таблицы 2.3
Методические указания При решении данной задачи необходимо прежде всего уяснить сущность аналогии тепловых и электрических явлений. Принцип составления тепловых схем замещения изложен в литературе (см. учебник § 7.1, § 9.1 - § 9.3 [1, с. 104-114, 167-1181]). Метод ЭТС имеет то преимущество, что для преобразования сложных схем замещения можно применять методы, разработанные для сложных электрических цепей, в частности, преобразование треугольника сопротивлений в эквивалентную звезду, параллельное и последовательное соединение сопротивлений. Причем никаких ограничений на преобразование ЭТС нет. Однако, между ЭТС и электрической цепью имеется и различия: 1. Электрические цепи изображается замкнутыми, а тепловые схемы разомкнутыми. 2.В электрических цепях известными являются приложенные напряжения, а необходимо определить токи в отдельных ответвлениях. В тепловых схемах решается обратная задача - известными являются тепловые потоки (аналог тока), а определить нужно перепады температуры (аналог падения напряжения). На первом этапе выполняется расчет термических сопротивлений, входящих в ЭТС. При расчете предполагается, что условия охлаждения лобовых частей обмотки якоря одинаковы. Не учитываем тепловые потоки, которые проходят через торцевые поверхности сердечника и через вал (их величина, как правило, незначительная). На пути тепловых потоков, исходящих от меди обмотки якоря (рис. 2.3) встречаются следующие термические сопротивления: RИ, RlЛ1 и RlЛ2 - полные термические сопротивления (ТС) теплопроводности изоляции соответственно пазовой части обмотки и лобовых частей в сторону бандажа и в сторону обмоткодержателя. Расчет их выполняется по известному выражению (формула 7.15 (см. учебник § 7.1 [1, с. 106])): Rli = ∙di /(li∙Si), где∙di – толщина изоляции в направлении соответствующего потока; Si – площадь поверхности изоляции на пути этих потоков; Коэффициент теплопроводности изоляции lI выбрать для класса В из приложения 4 учебника [1, с. 230] Rпа, Rка, RαЛ1 и RαЛ2 - полные ТС теплоотдачи изоляции соответственно с поверхности сердечника якоря, поверхности каналов якоря, поверхностей лобовых частей в сторону бандажа и в сторону обмоткодержателя. Расчет их выполняется по известному выражению (формула 7.19 (см. учебник § 7.1 [1, с. 107])): Rαi = ∙1/(αi∙Si), где∙αi – коэффициенты теплоотдачи в направлении соответствующего потока; Si – площадь теплоотдающей поверхности на пути этих потоков. Необходимые для расчета площади поверхностей в формулах рассчитываются по заданным в таблицах геометрическим размерам. Коэффициенты теплоотдачи с поверхности сердечника якоря и лобовых частей определяются по империческим формулам (см. учебник § 10.5 [1, с.213]) Коэффициенты теплоотдачи с поверхности каналов якоря рассчитывается по приближенной формуле: αК = αО(1+к∙√VК)∙(1+0.5∙а), где к – конструктивная константа (принять к=1.2); а – коэффициент подогрева воздуха при продуве через каналы. Величина а находится в пределах а = 0.1 – 0.3 ЭТС, полученная для якоря (рис. 2.4), должна быть преобразована к простейшему виду (рис. 2.5).
Рис. 2.5. Преобразованная ЭТС якоря машины постоянного тока
При преобразовании используется метод транспозиции (см. учебник § 9.3 [1, с.177-178]). При определении перегрева обмотки якоря
∆θма-в = (Рма + Рста∙ Rа/( Rа+ RИ))/(1/ RЛ+1/( Rа+ RИ)).
Рис. 2.6. Аналогичным образом определяется перегрев сердечника якоря
∆θст-в = (Рста + Рма∙ RЛ/( RЛ+ RИ))/(1/ RЛ+1/( RЛ+ RИ)). Рис. 2.7.
Примечание: 1. Класс нагревостойкости электроизоляционных материалов, примененных при изготовлении машин – класс В. 2. Номинальная частота вращения n=1500 об/мин
Контрольные вопросы 1. От каких факторов зависит эквивалентный коэффициент теплопроводности пазовой изоляции обмотки электрической машины? 2. Какое влияние оказывает пропитка обмотки статора на тепловое состояние электрической машины? 3. Охарактеризуйте наиболее эффективный способ пропитки обмотки статора? 4. Из каких перепадов температуры складывается перегрев обмотки масляных трансформаторов? 5. Какие меры можно принять для снижения нагрева обмотки трансформатора? 6. Как зависит удельное термическое сопротивление теплоотдачи плоской стенки от величины коэффициента теплоотдачи? 7. Зависит ли конвективный теплообмен только от интенсивности перемешивания неравномерно нагретых масс жидкостей? 8. Назовите факторы, влияющие на величину термического сопротивления теплопроводности. 9. От чего зависит термическое сопротивление теплоотдачи? 10. Запишите выражения для законов Фурье и Ньютона. Объясните физический смысл их составляющих. 11. Как определить перегрев обмотки якоря машины постоянного тока, используя метод транспозиции при преобразовании ЭТС? 12. Какие меры можно принять для снижения перегрева обмотки якоря?
Рекомендуемая литература а) Основная литература: 1. Сипайлов Г.А., Санников Д.И., Жадан В.А. Тепловые, гидравлические и аэродинамические расчеты в электрических машинах. М.: Высшая школа, 1989. 239 с. 2. Проектирование электрических машин: Учебник для вузов/И.П.Копылов, Б.К.Клоков, В.П.Морозкин, Б.Ф.Токарев; Под ред. И.П.Копылова. 3-е изд., испр. и доп. – М.; Высш. Шк., 2002. – 757 с. 3. А.В.Иванов-Смоленский. Электрические машины: Учебник для вузов. В двух томах. М.: Издательство МЭИ, 2004. 1170 с.
б) Дополнительная литература 1. Филиппов И.Н. Теплообмен в электрических машинах. Л.: Энергоатомиздат, Ленинградское отделение, 1986. 256 с. 2. Борисенко А.И., Данько В.Г., Яковлев А.И. Аэродинамика и теплопередача в электрических машинах. М.: Энергия, 1974. 560 с. 3. Борисенко А.И., Костиков О.Н., Яковлев А.И. Охлаждение промышленных электрических машин. М.: Энергоатомиздат, 1983. 296 с. 4. Идельчик И.Е. Справочник по гидравлическим сопротивлениям. М.: Машиностроение, 1975. 559 с. 5. Виноградов В.И. Вентиляторы электрических машин. Л.: Энергоиздат, 1981. 200 с. 6 Жерве Г.К. Промышленные испытания электрических машин. Л.: Энергоатомиздат, 1984. 408 с. 7. Гуревич Э.И. Тепловые испытания и исследования электрических машин. Л.: Энергия, 1977. 296 с. 8. Алексеев А.Е. Конструкция электрических машин. М., Л.: Госэнергоиздат, 1958. 426 с. 9. Гурин Я.С., Курочкин М.П. Проектирование машин постоянного тока. М., Л.: Госэнергоиздат, 1961. 351 с. 10. Жадан В.А. Вентиляционный расчет электрических машин: Методические указания к выполнению домашнего задания по курсу “Тепловые, гидравлические и аэродинамические расчеты электрических машин” для студентов специальности 0601. Томск: изд. ТПИ им.С.М.Кирова, 1986. 33 с. 11. Жадан В.А., Денисенко В.И. Тепловые расчеты электрических машин: Вопросы, задачи и методические указания по выполнению контрольной работы по курсу “Тепловые, гидравлические и аэродинамические расчеты в электрических машинах” для студентов всех форм обучения специальности 180100 - “Электромеханика”. Свердловск: УПИ, 1990. 24 с.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,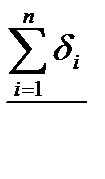 с эквивалентным коэффициентом теплопроводности lэкв. Результирующее удельное термическое сопротивление такой изоляции будет равно
с эквивалентным коэффициентом теплопроводности lэкв. Результирующее удельное термическое сопротивление такой изоляции будет равно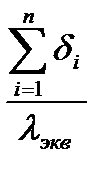 .
.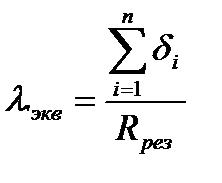
 θО
θО 
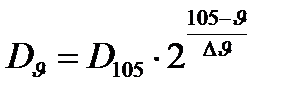 лет,
лет,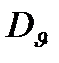 - срок службы; при температуре θ;
- срок службы; при температуре θ;